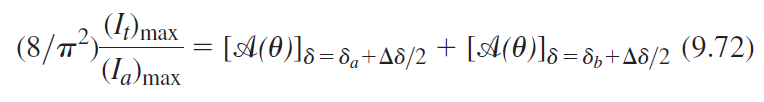![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


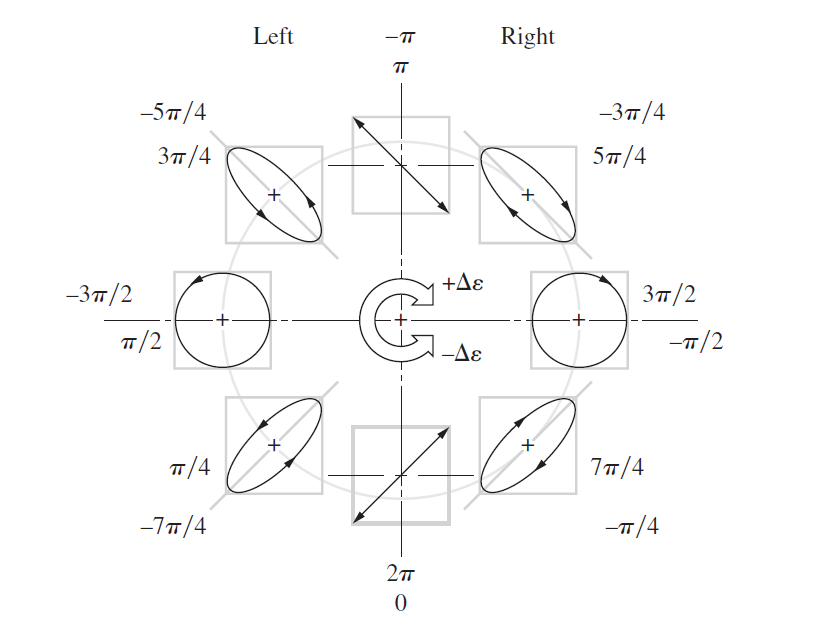

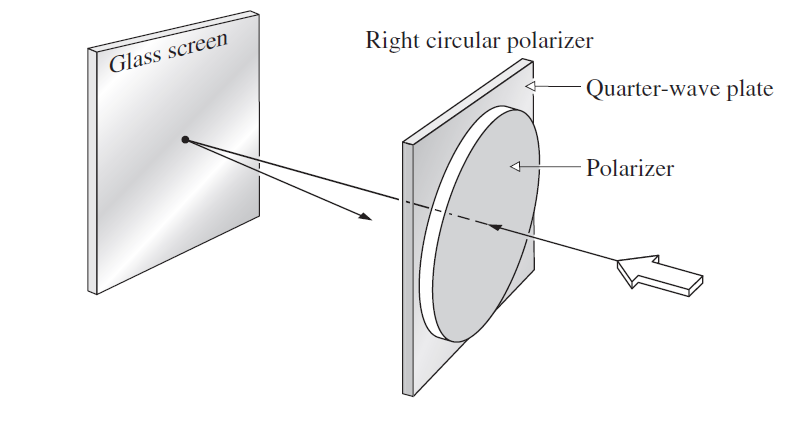

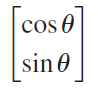
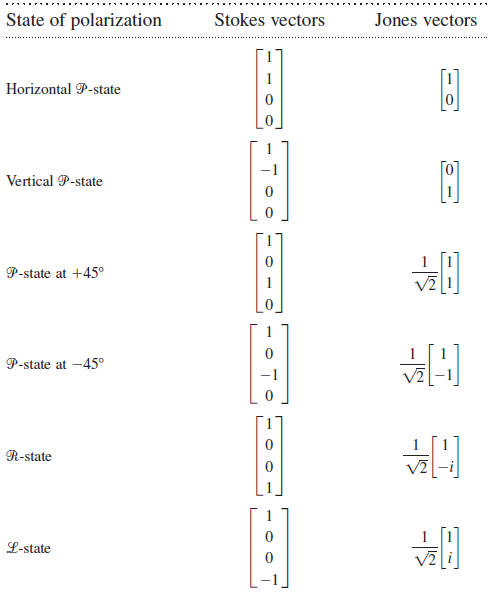
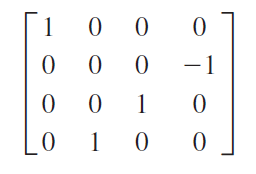
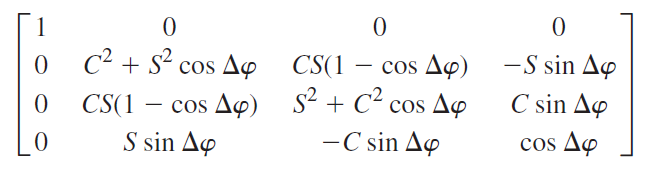
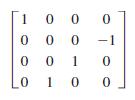
![Linear optical element Jones matrix Mueller matrix 1 [1 o] Horizontal linear polarizer 1 -1 1 -1 Vertical linear polariz](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1546/9/6/3/4285c34c9e48c23c1546946044802.jpg)
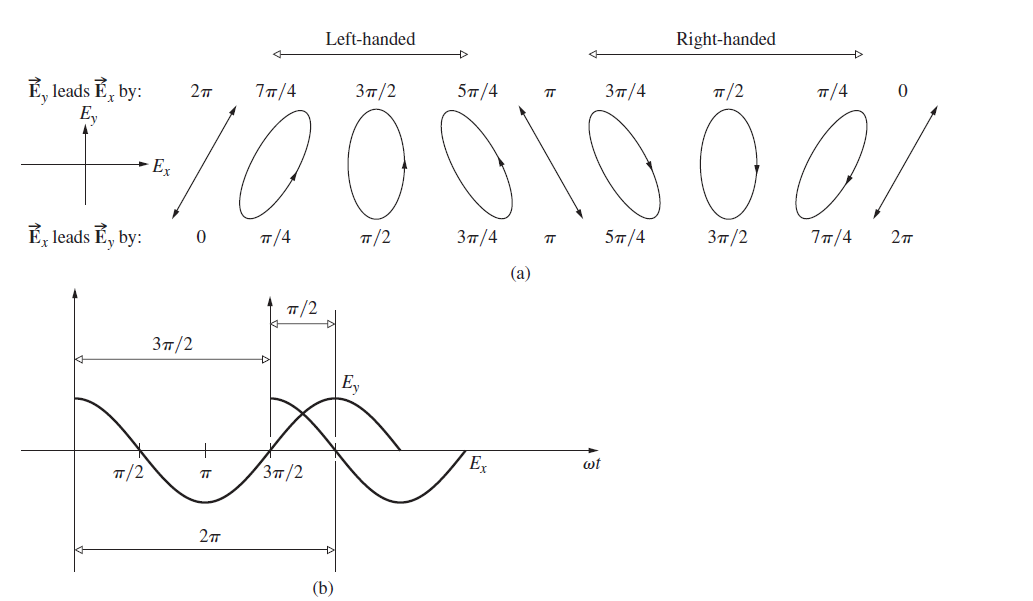

![TABLE 8.6 Jones and Mueller Matrices Linear optical element Jones matrix Mueller matrix [1 0] Horizontal linear polarizer 20 -1 Vertical linear [o o] 1 -1 1 polarizer 1 Linear polarizer 10 at +45° 21 1 1 -1 Linear polarizer at -45° 2 -1 1 [1 Quarter-wave plate, fast axis](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1607/6/6/8/4665fd312f2618cb1607668465250.jpg)

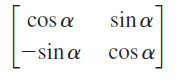
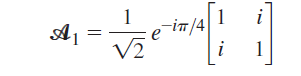
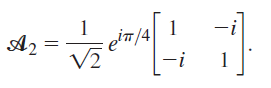
![[1+ V3 2V2 1 ] -1 + V3 1+ V3 [1 - V3](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1546/9/6/4/8405c34cf68b66c41546947456691.jpg)
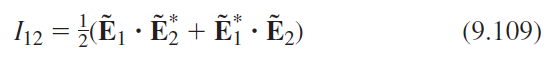
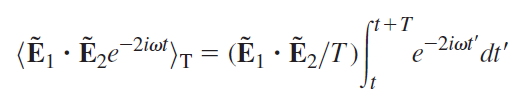
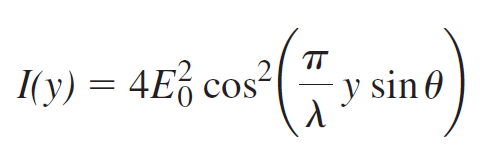
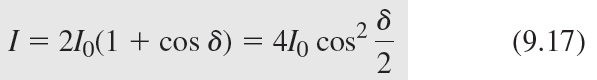
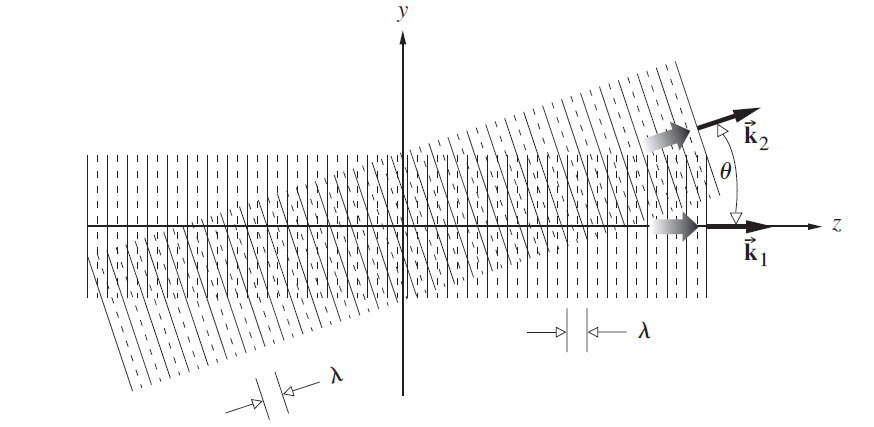
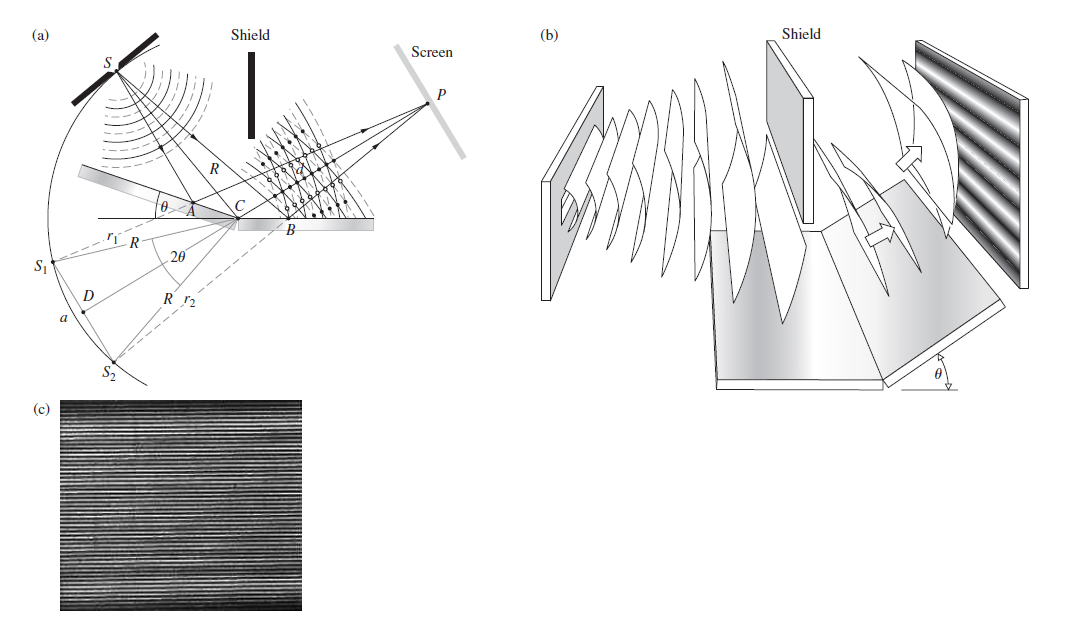
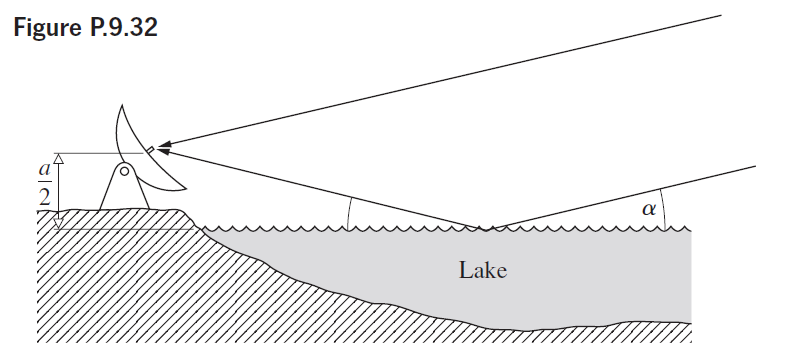
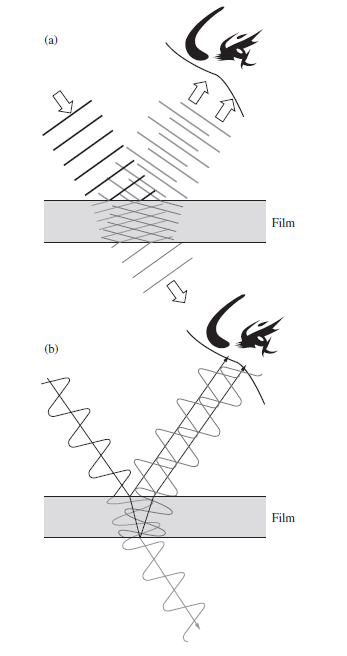
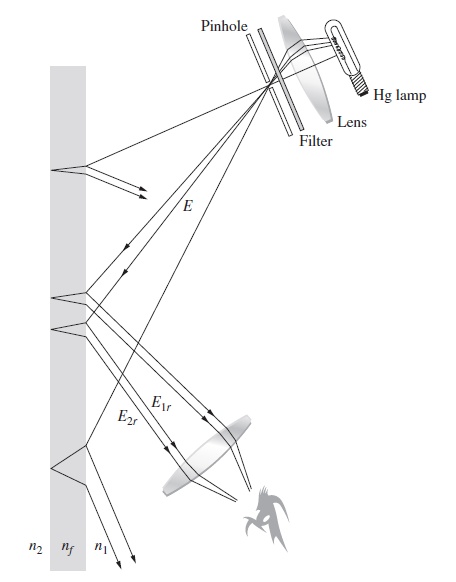
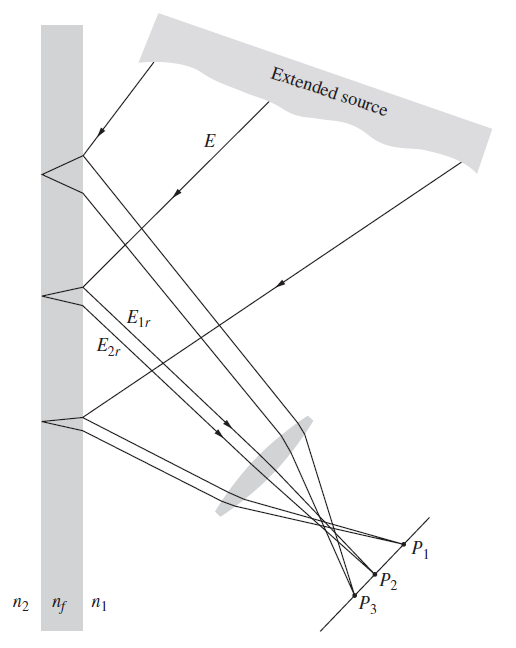
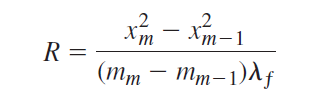
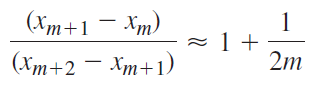
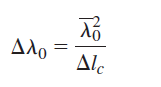
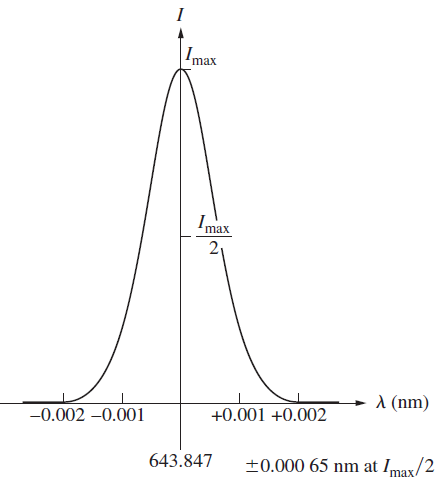
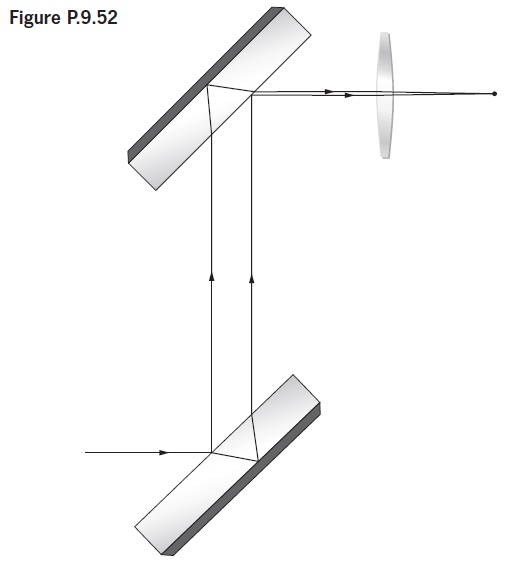
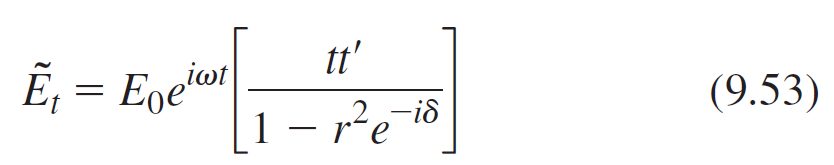
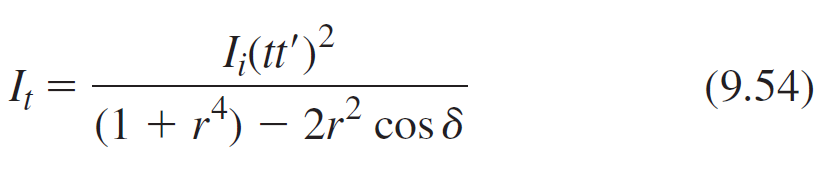
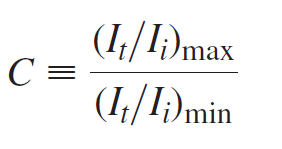
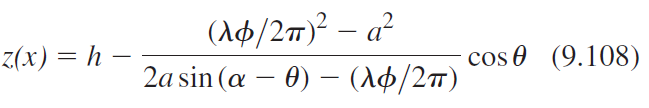
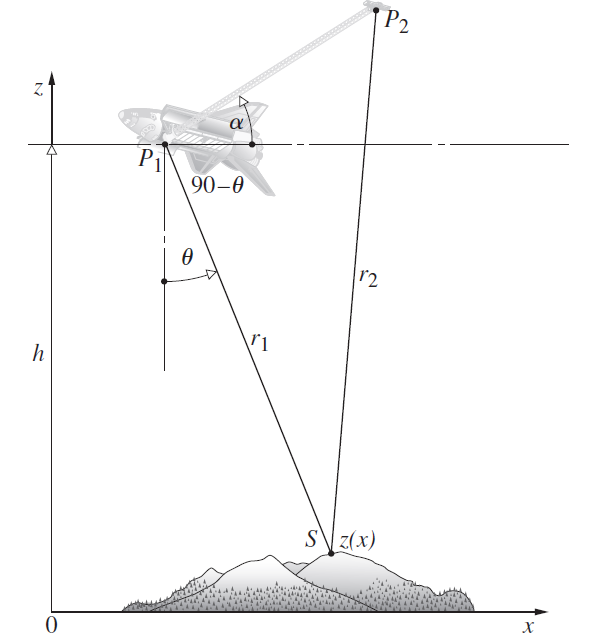
![4.2/VF (A8) [9.73]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1547/0/4/2/3225c35fe1239e5e1547024945435.jpg)
![[A(0)]s=8±A8/2 = [A(0)]s=A8/2](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1547/0/4/2/3385c35fe223eba71547024961592.jpg)