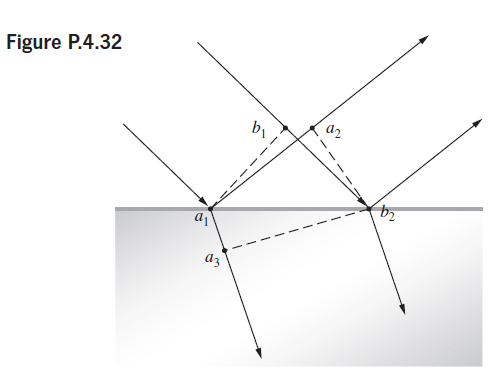
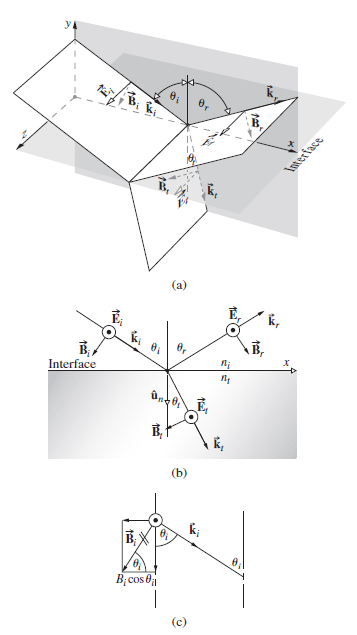
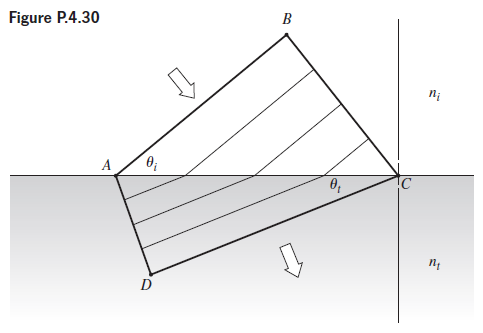
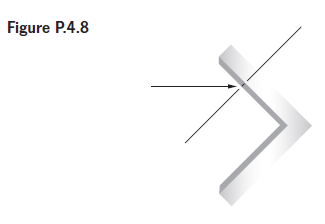
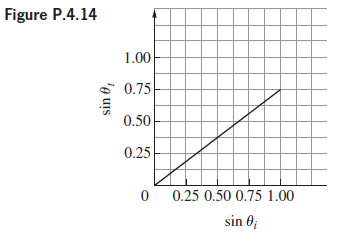
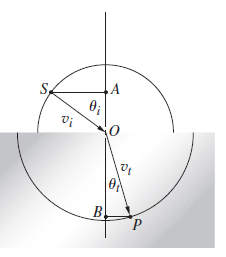
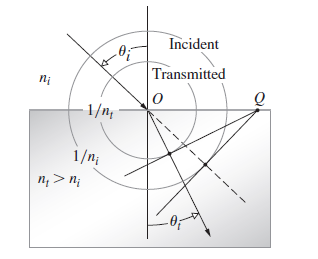
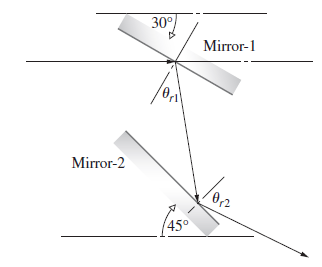
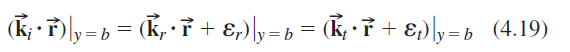![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


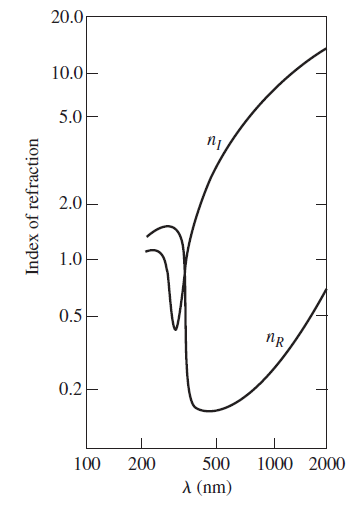
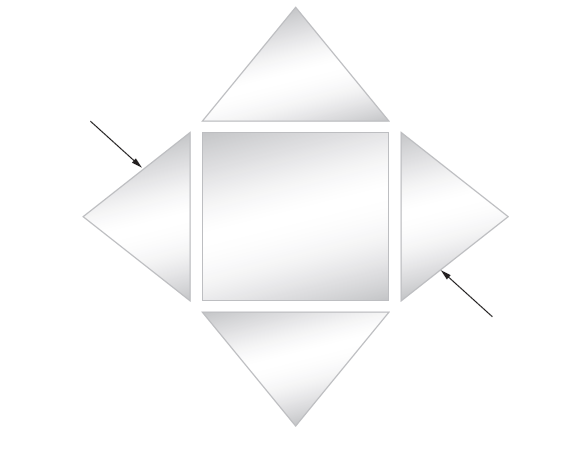
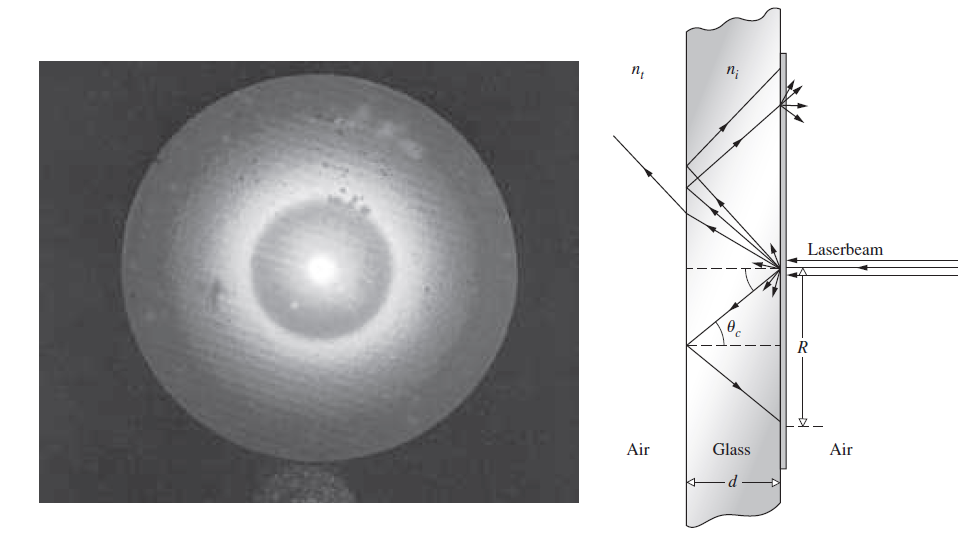
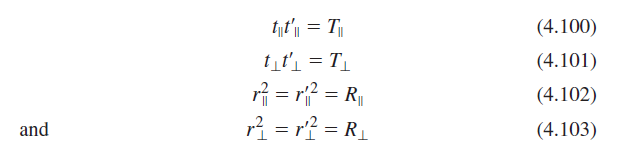
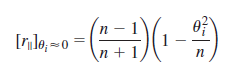
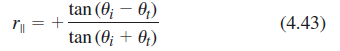

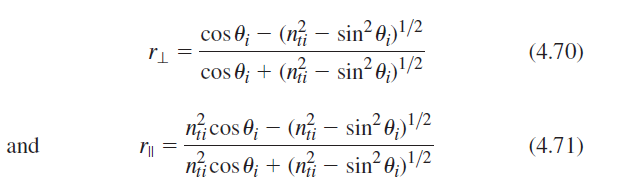
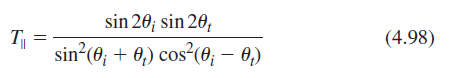
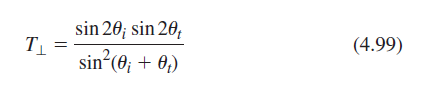
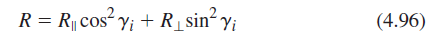
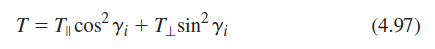
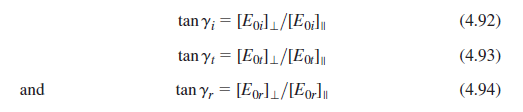
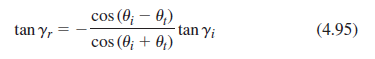
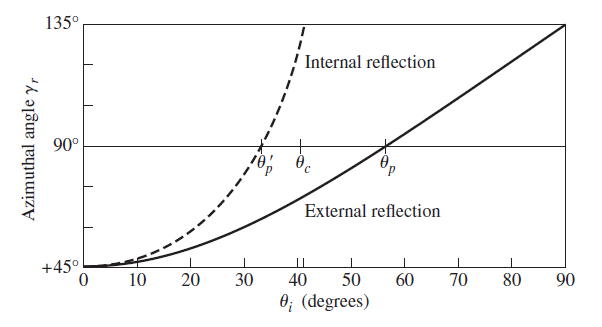
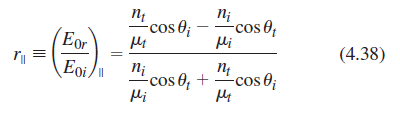
![[4.49] ti +(-r1) = 1](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1546/3/4/2/3255c2b4fb58f53d1546324930909.jpg)
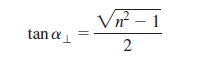
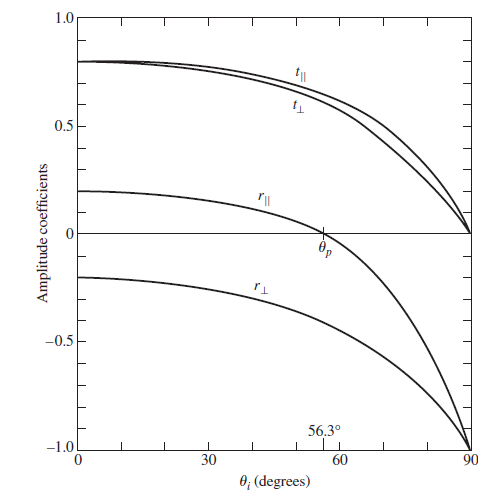
![sin (0; – 0,) [4.42] sin (0; + 0,)](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1546/3/4/1/6445c2b4d0c5584e1546324249881.jpg)
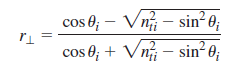
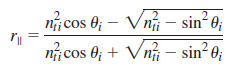
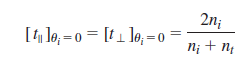
![sin (0; – 0,) [4.42] sin (0; + 0,) ||](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1607/6/6/6/7905fd30c6696cf81607666789588.jpg)
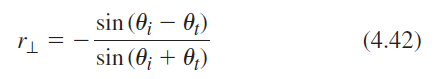

![n, k, – n;k = (n,cos 0; – n;cos 0;) û, [4.7]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1546/3/3/9/3305c2b4402152fa1546321935409.jpg)