Programming Language Pragmatics 4th Edition Michael L. Scott - Solutions

Consider the person_interface and system_user_interface classes described in Example C 10.62. If student is derived from person_interface and system_ user_interface, explain what happens in the following method call:student s;person *p = &s;...p->print_stats();You may wish to use a diagram
Given the inheritance tree of Example C 10.63, show a representation for objects of class student_prof. You may want to consult Figures C 10.9, C 10.10, and C 10.11.
Given the memory layout of Figure C 10.9 and the following declarations:student& sr;system_user& ur;show the code that must be generated for the assignmentur = sr;(Pitfall: Be sure to consider null pointers.)
Standard C++ provides a “pointer-to-member” mechanism for classes:Pointers to members are also permitted for subroutine members (methods), including virtual methods. How would you implement pointers to virtual methods in the presence of C++-style multiple inheritance? class C { public: int a;
As an alternative to using hmethod address, this correctioni pairs in the vtable entries of a language withmultiple inheritance, we could leave the entries as simple pointers, but make them point to code that updates this in-line, and then jumps to the beginning of the appropriate method, much as
In Eiffel, shared inheritance is the default rather than the exception. Only renamed features are replicated. As a result, it is not possible to tell when looking at a class whether its members will be inherited replicated or shared by derived classes. Describe a uniform mechanism for looking up
In Figure C 10.11, consider calls to virtual methods declared in A, but called through a B, C, or D object view. We could avoid one level of indirection by appending a copy of the A part of the vtable to the D/B and C parts of the vtable (with suitably adjusted this corrections). Give calling
Consider the Smalltalk implementation of Euclid’s algorithm, presented at the end of Section C 10.7.1. Trace the messages involved in evaluating 4 gcd: 6.
Is the define primitive of Scheme an imperative language feature? Why or why not?
It is possible to write programs in a purely functional subset of an imperative language such as C, but certain limitations of the language quickly become apparent. What features would need to be added to your favorite imperative language to make it genuinely useful as a functional language?
Explain the connection between short-circuit Boolean expressions and normal-order evaluation. Why is cond a special form in Scheme, rather than a function?
Write a program in your favorite imperative language that has the same input and output as the Scheme program of Figure 11.1. Can you make any general observations about the usefulness of Scheme for symbolic computation, based on your experience?Figure 11.1 (define simulate (lambda (dfa input)
Suppose we wish to remove adjacent duplicate elements from a list (e.g., after sorting). The following Scheme function accomplishes this goal:Write a similar function that uses the imperative features of Scheme to modify L “in place,” rather than building a new list. Compare your function to
Write tail-recursive versions of the following:(a)(b) ;; compute integer log, base 2 ;; (number of bits in binary representation) ;; works only for positive integers (define log2 (lambda (n) (if (= n 1) 1 (+ 1 (log2 (quotient n 2))))))
Write purely functional Scheme functions to(a) Return all rotations of a given list. For example, (rotate ‚(a b c d e)) should return ((a b c d e) (b c d e a) (c d e a b) (d e a b c) (e a b c d)) (in some order).(b) Return a list containing all elements of a given list that satisfy a given
Write a purely functional Scheme function that returns a list of all permutations of a given list. For example, given (a b c), it should return ((a b c) (b a c) (b c a) (a c b) (c a b) (c b a)) (in some order).
Modify the Scheme program of Figure 11.1 or the OCaml program of Figure 11.3 to simulate an NFA (nondeterministic finite automaton), rather than a DFA. (The distinction between these automata is described in Section 2.2.1.) Since you cannot “guess” correctly in the face of a multivalued
Consider the problem of determining whether two trees have the same fringe: the same set of leaves in the same order, regardless of internal structure. An obvious way to solve this problem is to write a function flatten that takes a tree as argument and returns an ordered list of its leaves. Then
In Example 11.59 we showed how to implement interactive I/O in terms of the lazy evaluation of streams. Unfortunately, our code would not work as written, because Scheme uses applicative-order evaluation. We can make it work, however, with calls to delay and force.Suppose we define input to be a
Write new versions of cons, car, and cdr that operate on streams. Using them, rewrite the code of the previous exercise to eliminate the calls to delay and force. Note that the stream version of cons will need to avoid evaluating its second argument; you will need to learn how to define macros
Write the standard quicksort algorithm in Scheme, without using any imperative language features. Be careful to avoid the trivial update problem; your code should run in expected time n log n.Rewrite your code using arrays (you will probably need to consult a Scheme manual for further information).
Write insert and find routines that manipulate binary search trees in Scheme (consult an algorithms text if you need more information). Explain why the trivial update problem does not impact the asymptotic performance of insert.
Write an LL(1) parser generator in purely functional Scheme. If you consult Figure 2.24, remember that you will need to use tail recursion in place of iteration. Assume that the input CFG consists of a list of lists, one per nonterminal in the grammar. The first element of each sublist should be
Write an equality operator (call it =/) that works correctly on the yearday type of Example 11.38. (You may need to look up the rules that govern the occurrence of leap years.)
Create addition and subtraction functions for the celsius and fahrenheit temperature types introduced in Sidebar 11.3. To allow the two scales to be mixed, you should also define conversion functions ct_of_ft : fahrenheit_temp -> celsius_temp and ft_of_ct : celsius_temp -> fahrenheit_temp.
We can use encapsulation within functions to delay evaluation in OCaml:Now givenlet rec next_int n = (n, Promise (fun() -> next_int (n + 1)));;let naturals = Promise (fun() -> next_int (1));;we havehead naturals;;
Write an OCaml version of Example 11.67. Alternatively (or in addition), solve Exercises 11.5, 11.7, 11.8, 11.10, 11.13, 11.14, or 11.15 in OCaml.
In Figure C 11.6 we evaluated our expression in normal order. Did we really have any choice? What would happen if we tried to use applicative order?
Prove that for any lambda expression f , if the normal-order evaluation of Y f terminates, where Y is the fixed-point combinator λh:(λx:h(x x)) (λx:h(x x)), then f (Yf ) and Yf will reduce to the same simplest form.
Given the definition of structures (lists) in Section C 11.7.3, what happens if we apply car or cdr to nil? How might you introduce the notion of “type error” into lambda calculus?
Letzero Ξ λx:xsucc Ξ λn:(λs:(s select second) n)where select second Ξ λx:λy:y. Now letone Ξ succ zerotwo Ξ succ one
Starting with the clauses at the beginning of Example 12.17, use resolution (as illustrated in Example 12.3) to show, in two different ways, that there is a path from a to e.
Solve Exercise 6.22 in Prolog.Data From Exercise 6.22:Use iterators to construct a program that outputs (in some order) all structurally distinct binary trees of n nodes. Two trees are considered structurally distinct if they have different numbers of nodes or if their left or right subtrees are
Consider the Prolog gcd program in Figure 1.2. Does this program work “backward” as well as forward? (Given integers d and n, can you use it to generate a sequence of integers m such that gcd(n, m) = d?) Explain your answer.Figure 1.2: int gcd(int a, int b) { // C while (a != b) { if (a > b) a
In the spirit of Example 11.20, write a Prolog program that exploits backtracking to simulate the execution of a nondeterministic finite automaton.
Show that resolution is commutative and associative. Specifically, if A, B, and C are Horn clauses, show that (A ⊕B) = (B ⊕ A) and that ((A ⊕ B) ⊕ C) = (A ⊕ (B ⊕ C)), where ⊕ indicates resolution. Be sure to think about what happens to variables that are instantiated as a result of
In Example 12.8, the query ?- classmates(jane_doe, X) will succeed three times: twice with X = jane_doe and once with X = ajit_chandra. Show how to modify the classmates(X, Y) rule so that a student is not considered a classmate of himself or herself.
Modify Example 12.17 so that the goal path(X, Y), for arbitrary already instantiated X and Y, will succeed no more than once, even if there are multiple paths from X to Y.
Using only \+ (no cuts), modify the tic-tac-toe example of Section 12.2.5 so it will generate only one candidate move from a given board position. How does your solution compare to the cut-based one (Example 12.22)?
Prove the claim, made in Example 12.19, that there is no winning strategy in tic-tac-toe—that either player can force a draw.
Prove that the tic-tac-toe strategy of Example 12.19 is optimal (wins against an imperfect opponent whenever possible, draws otherwise), or give a counterexample.
Starting with the tic-tac-toe program of Figure 12.4, draw a directed acyclic graph in which every clause is a node and an arc from A to B indicates that it is important, either for correctness or efficiency, that A come before B in the program. (Do not draw any other arcs.) Any topological sort of
Write Prolog rules to define a version of the member predicate that will generate all members of a list during backtracking, but without generating duplicates. Note that the cut and\+ based versions of Example 12.20 will not suffice; when asked to look for an uninstantiated member, they find only
Use the clause predicate of Prolog to implement the call predicate (pretend that it isn’t built in). You needn’t implement all of the built-in predicates of Prolog; in particular, you may ignore the various imperative control-flow mechanisms and database manipulators. Extend your code by making
Use the clause predicate of Prolog to write a predicate call_bfs that attempts to satisfy goals breadth-first.
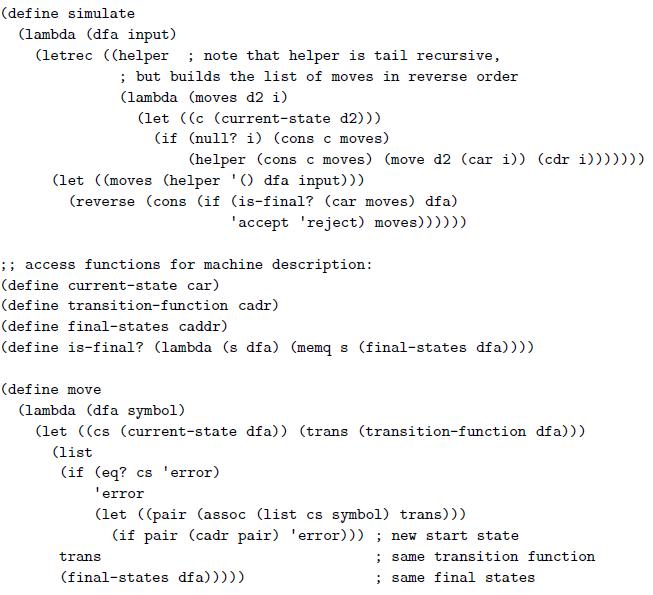
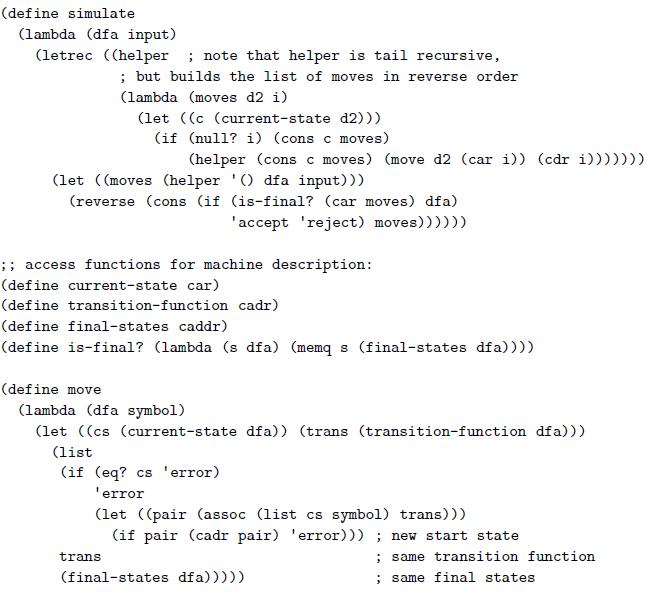
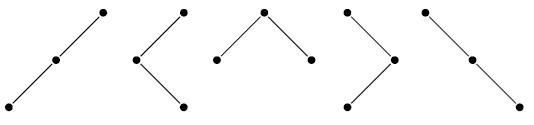
Write a (list-based) insertion sort algorithm in Prolog. Here’s what it looks like in C, using arrays: void insertion_sort(int A[], int N) int i, j, t; for (i = 1; i < N; i++) { %3D t = A[i]; for (j = i; j > 0; j--) { if (t >= A[j-1]) break; A[j] A[j-1]; A[j] = t; } $void insertion_sort(int A[], int N) int i, j, t; for (i = 1; i < N; i++) { %3D t = A[i]; for (j = i; j style=$
Quicksort works well for large lists, but has higher overhead than insertion sort for short lists. Write a sort algorithm in Prolog that uses quicksort initially, but switches to insertion sort (as defined in the previous exercise) for sublists of 15 or fewer elements.
Write a Prolog sorting routine that is guaranteed to take O(n log n) time in the worst case.
Consider the following interaction with a Prolog interpreter:?- Y = X, X = foo(X).Y =
Restate the following Prolog rule in predicate calculus, using appropriate quantifiers:sibling(X, Y) :- mother(M, X), mother(M, Y), father(F, X), father(F, Y).
Consider the following statement in predicate calculus:empty_class(C) ← ¬∃X[takes(X; C)](a) Translate this statement to clausal form.(b) Can you translate the statement into Prolog? Does it make a difference whether you’re allowed to use \+?(c) How about the following:takes
Consider the seemingly contradictory statement¬foo(X) → foo(X)Convert this statement to clausal form, and then translate into Prolog. Explain what will happen if you ask?- foo(bar).Now consider the straightforward translation, without the intermediate conversion to clausal form:foo(X) :-
Write a simple abstract ordered_set class (an interface) whose methods include void insert(T val), void remove (T val), bool lookup (T val), and bool is_empty(), together with a language-appropriate iterator, as described in Section 6.5.3. Using this abstract class as a base, build a simple
C++ has no direct analogue of the extends X and super X clauses of Java. Why not?
Modify the code of Figure 7.3 or your solution to Exercise 7.12 to throw an exception if an attempt is made to enqueue an item in a full queue, or to dequeue an item from an empty queue.Data From Exercise 7.12:Figure 7.3 passes integer max_items to the queue abstraction as a generic parameter. $template class queue { item items [max_items]; int next_free, next_full, num_items; public: queue () : next_free(0), next_full(0), num_items (0) { } bool enqueue (const item& it) { if (num_items == max_items) return false; ++num_items; items [next_free] it; next_free (next_free + 1) % max_items; %3D return true; bool dequeue (item* it)$
In Section 9.3.1 we noted that Ada 83 does not permit subroutines to be passed as parameters, but that some of the same effect can be achieved with generics. Suppose we want to apply a function to everymember of an array.We might write the following in Ada 83:Given an array of integers, scores, and
Bjarne Stroustrup, the original designer of C++, once described templates as “a clever kind of macro that obeys the scope, naming, and type rules of C++” [Str13, 2nd ed., p. 257]. How close is the similarity? What can templates do that macros can’t? What do macros do that templates don’t?
Consider the following code skeleton in C++:Explain why the compiler won’t allow the second call. Give an example of bad things that could happen if it did. #include using std::1ist; class foo {... class bar : public foo { ... static void print_all(list &L) { .. list LF; list LB; print_all (LF); $#include using std::1ist; class foo {... class bar : public foo { ... static void print_all(list &L) { .. list LF; list LB; print_all (LF); print_all (LB); // works fine // static semantic error$
Yet another solution to the problem of the previous exercise is to make the sorting routine a method of a sorter class. The comparison routine can then be passed into the class as a constructor argument. Implement this option and compare it to those of the previous exercise.
In Example 7.53 we mentioned three ways to make the need for comparisons more explicit when defining a generic sort routine in C++: make the comparison routine a method of the generic parameter class T, an extra argument to the sort routine, or an extra generic parameter. Implement these options
Flesh out the C++ sorting routine of Example 7.53. Demonstrate that this routine does “the wrong thing” when asked to sort an array of char* strings.
Rewrite the generic sorting routine of Examples 7.50–7.52 (with constraints) using OCaml or SML functors.
Figure 7.3 passes integer max_items to the queue abstraction as a generic parameter. Write an alternative version of the code that makes max_items a parameter to the queue constructor instead. What is the advantage of the generic parameter version?Figure 7.3: template class queue { item items $template class queue { item items [max_items]; int next_free, next_full, num_items; public: queue () : next_free(0), next_full(0), num_items (0) { } bool enqueue (const item& it) { if (num_items == max_items) return false; ++num_items; items [next_free] it; next_free (next_free + 1) % max_items; %3D return true; bool dequeue (item* it)$
In your favorite language with generics, write code for simple versions of the following abstractions:(a) A stack, implemented as a linked list(b) A priority queue, implemented as a skip list or a partially ordered tree embedded in an array(c) A dictionary (mapping), implemented as a hash table
(a) Give a generic solution to Exercise 6.19.Data From Exercise 6.19:Write a C++ preorder iterator to supply tree nodes to the loop in Example 6.69. You will need to know (or learn) how to use pointers, references, inner classes, and operator overloading in C++. For the sake of (relative)
Rewrite the code of Figure 7.3 in Ada, Java, or C#.Figure 7.3: template class queue { item items [max_items]; int next_free, next_full, num_items; public: queue () : next_free (0), next_full(0), num_items (0) { } bool enqueue (const item& it) { if (num_items ++num_items; items [next_free] == $template class queue { item items [max_items]; int next_free, next_full, num_items; public: queue () : next_free (0), next_full(0), num_items (0) { } bool enqueue (const item& it) { if (num_items ++num_items; items [next_free] == max_items) return false; it; next_free (next_free + 1) % max_items; return true; } bool dequeue (item*$
In Section 7.2.2 we introduced the notion of a universal reference type (void * in C) that refers to an object of unknown type. Using such references, implement a “poor man’s generic queue” in C, as suggested in Section 7.3.1. Where do you need type casts? Why? Give an example of a use of the
Consider the problem of performing range checks on set expressions in Pascal. Given that a set may contain many elements, some of which may be known at compile time, describe the information that a compiler might maintain in order to track both the elements known to belong to the set and the
Ada provides two “remainder” operators, rem and mod for integer types, defined as follows [Ame83, Sec. 4.5.5]:Integer division and remainder are defined by the relation A = (A/B)*B + (A rem B), where (A rem B) has the sign of A and an absolute value less than the absolute value of B. Integer
When Sun Microsystems ported Berkeley Unix from the Digital VAX to the Motorola 680x0 in the early 1980s,many C programs stopped working, and had to be repaired. In effect, the 680x0 revealed certain classes of program bugs that one could “get away with” on the VAX. One of these classes of bugs
Suppose you are implementing an Ada compiler, and must support arithmetic on 32-bit fixed-point binary numbers with a programmer-specified number of fractional bits. Describe the code you would need to generate to add, subtract, multiply, or divide two fixed-point numbers. You should assume that
Consider the following declarations:1. type cell –– a forward declaration2. type cell_ptr = pointer to cell3. x : cell4. type cell = record5. val : integer6. next : cell ptr7. y : cellShould the declaration at
In the following code, which of the variables will a compiler consider to have compatible types under structural equivalence? Under strict name equivalence? Under loose name equivalence?type T = array [1..10] of integer S = TA : TB : TC : SD : array [1..10] of
Most statically typed languages developed since the 1970s (including Java, C#, and the descendants of Pascal) use some form of name equivalence for types. Is structural equivalence a bad idea? Why or why not?
Write, in SR or pseudocode, a function that returns(a) An arbitrary nonzero element of a given array(b) An arbitrary permutation of a given arrayIn each case, write your code in such a way that if the implementation of nondeterminism were truly random, all correct answers would be equally likely.
The astute reader may have noticed that the final line of the code in Example C 6.95 embodies an arbitrary choice. It could just as easily have said gcd := b. Show how to use a guarded command to restore the symmetry of the program.
Explain why the following guarded commands in SR are not equivalent: if a < b -> c := a [] b < c ->c := b if a < b -> c := a [] b < c -> c := b %3D [] else ->c := d [] true -> c:= d fi fi
Write a findRE generator in Icon that mimics the behavior of find, but takes as its first parameter a regular expression. Use a string to represent your regular expression, with syntax as in Section 2.1.1. Use empty parentheses to represent ∈. Give highest precedence to Kleene closure, then
Write a program in Icon that will print the k most common words in its input, one per line, with each preceded by a count of the number of times it appears. If parameter k is not specified on the command line, use 10 by default. You will want to consult the Icon manual (available online [GG96]). In
(Difficult) Use call-with-current-continuation (call/cc) to implement the following structured nonlocal control transfers in Scheme. (This requires knowledge of material in Chapter 11.) You will probably want to consult a Scheme manual for documentation not only on call/cc, but on define-syntax and
Use lazy evaluation (delay and force) to implement iterator objects in Scheme. More specifically, let an iterator be either the null list or a pair consisting of an element and a promise which when forced will return an iterator. Give code for an uptoby function that returns an iterator, and a
Give an example in C in which an in-line subroutine may be significantly faster than a functionally equivalent macro. Give another example in which the macro is likely to be faster.
Is it possible to write a tail-recursive version of the classic quicksort algorithm? Why or why not?
Write a tail-recursive function in Scheme or ML to compute n factorial (n! = П1≤i≤n i = 1 × 2 × · · · × n).
Show how to calculate the number of iterations of a general Fortran 90- style do loop. Your code should be written in an assembler-like notation, and should be guaranteed to work for all valid bounds and step sizes.
If you have taken a course in automata theory or recursive function theory, explain why while loops are strictly more powerful than for loops. (If you haven’t had such a course, skip this question!) Note that we’re referring here to Ada-style for loops, not C-style.
A loop invariant is a condition that is guaranteed to be true at a given point within the body of a loop on every iteration. Loop invariants play a major role in axiomatic semantics, a formal reasoning system used to prove properties of programs. In a less formal way, programmers who identify (and
Bentley [Ben00, Chap. 4] provides the following informal description of binary search:We are to determine whether the sorted array X[1..N] contains the element T. . . . Binary search solves the problem by keeping track of a range within the array in which T must be if it is anywhere in the array.
Rubin [Rub87] used the following example (rewritten here in C) to argue in favor of a goto statement:The intent of the code is to find the first all-zero row, if any, of an n × n matrix. Do you find the example convincing? Is there a good structured alternative in C? In any language? int $int first_zero_row = -1; int i, j; /* none */ for (i = 0; i < n; i++) { for (j = 0; j < n; j++) { if (A[i] [j]) goto next; } first_zero_row = i; break; next: ; }$
Consider a mid-test loop, here written in C, that looks for blank lines in its input:Show how you might accomplish the same task using a while or do (repeat) loop, if mid-test loops were not available. How do these alternatives compare to the mid-test version? for (;;) { line read_line(); %3D if $for (;;) { line read_line(); %3D if (all_blanks (line)) break; consume_line (line); }$
In an expression-oriented language such as Algol 68 or Lisp, a while loop (a do loop in Lisp) has a value as an expression. How do you think this value should be determined? (How is it determined in Algol 68 and Lisp?) Is the value a useless artifact of expression orientation, or are there
Build true iterators in Java using threads. Make your solution as clean and as general as possible. In particular, you should provide the standard Iterator or IE numerable interface, for use with extended for loops, but the programmer should not have to write these. Instead, he or she should write
Use iterators to construct a program that outputs (in some order) all structurally distinct binary trees of n nodes. Two trees are considered structurally distinct if they have different numbers of nodes or if their left or right subtrees are structurally distinct. There are, for example, five
Write, in C#, Python, or Ruby, an iterator that yields (a) all permutations of the integers 1 . . n, (b) all combinations of k integers from the range 1 . . n (0 ≤ k ≤ n).You may represent your permutations and combinations using either a list or an array.
Write code for the tree_iter type (struct) andthe ti_create, ti_done, ti_next, ti_val, and ti_delete functions employed in Example 6.73.
Write a C++ preorder iterator to supply tree nodes to the loop in Example 6.69. You will need to know (or learn) how to use pointers, references, inner classes, and operator overloading in C++. For the sake of (relative) simplicity, you may assume that the data in a tree node is always an int; this
Revise the algorithm of Figure 6.6 so that it performs an in-order enumeration, rather than preorder.Figure 6.6: class BinTree implements Iterable { BinTree left; BinTree right; T val; // other methods: insert, delete, lookup, ... public Iterator iterator () { return new TreeIterator (this);
The equivalence of for and while loops, is not precise. Give an example in which it breaks down.
As noted in Section 6.4.2, languages vary in how they handle the situation in which the controlling expression in a case statement does not appear among the labels on the arms. C and Fortran 90 say the statement has no effect. Pascal and Modula say it results in a dynamic semantic error. Ada says
Consider the following expression in C: a/b > 0 && b/a > 0. What will be the result of evaluating this expression when a is zero? What will be the result when b is zero? Would it make sense to try to design a language in which this expression is guaranteed to evaluate to false when

Showing 600 - 700 of 817

Programming Language Pragmatics 4th Edition Michael L. Scott - Solutions

Step by Step Answers