![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


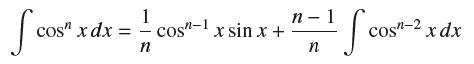
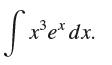
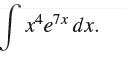
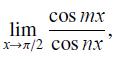
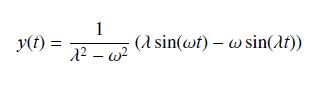
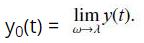
![f(x) = 1 x2 [1,4]](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/7/4/0/205655f3c6dcdfa31700740206492.jpg)
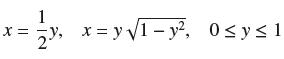
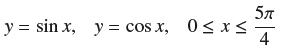
![f(x) = 2 x + 1' [1,3]](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/7/4/0/309655f3cd59699d1700740310422.jpg)
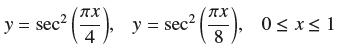


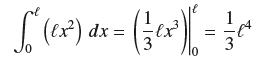
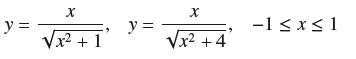
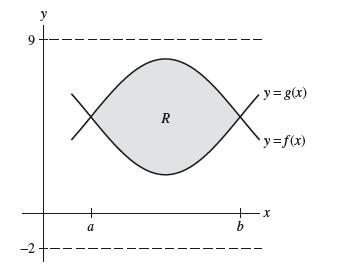
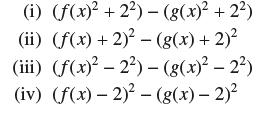
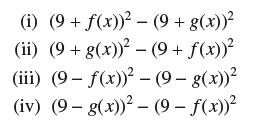
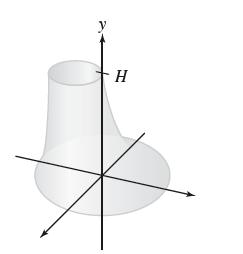

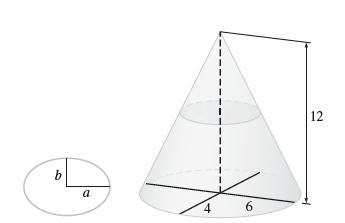
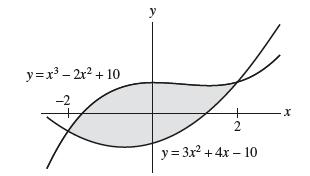
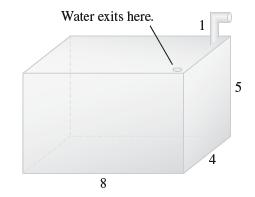
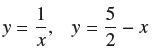

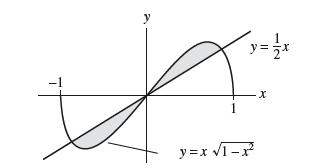
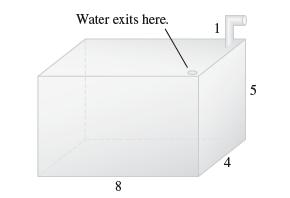
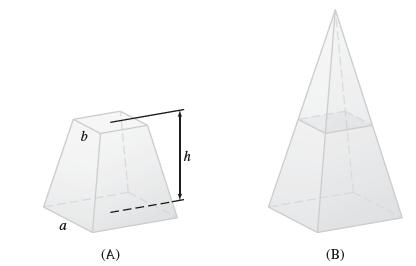
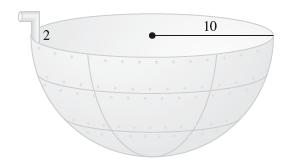
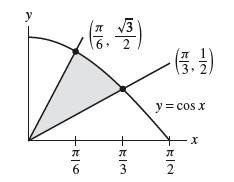
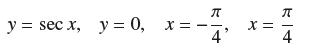

![f(x) = 1 x + 1 [0, 2], about x = 0](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/8/1/3/81365605bf59151b1700813812987.jpg)