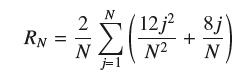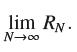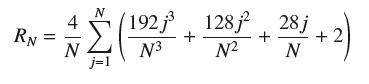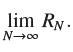![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


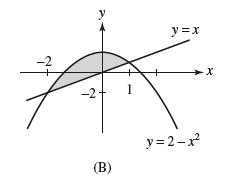
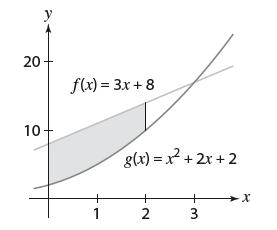
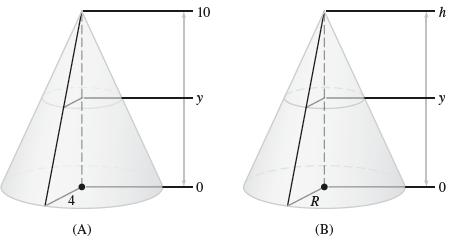
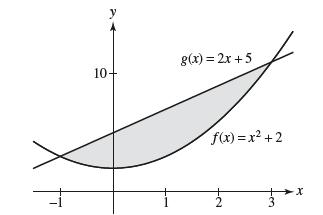
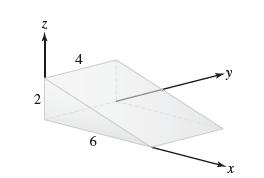
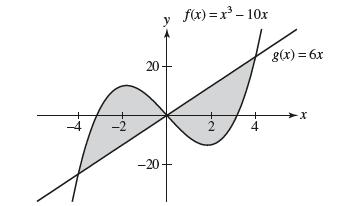
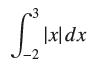
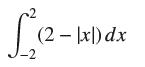
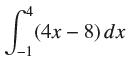
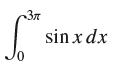
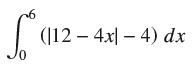
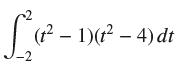
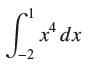
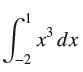
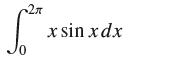
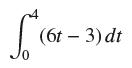
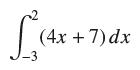
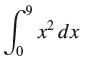
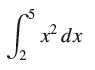
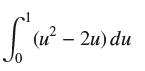
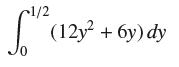
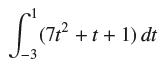
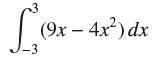
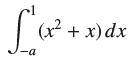
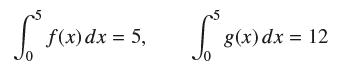
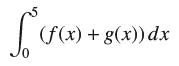
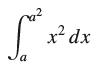
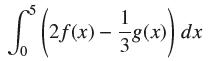
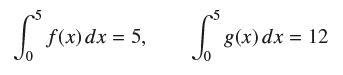
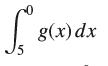
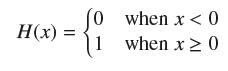
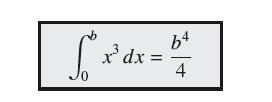

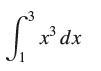
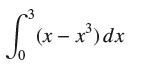
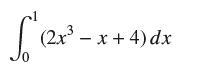
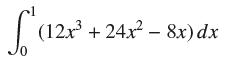
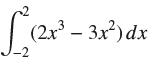
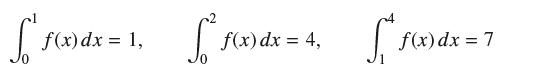
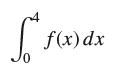
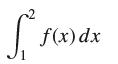
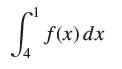
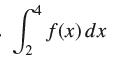
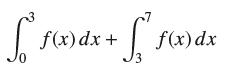
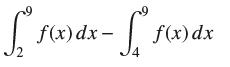
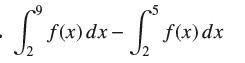
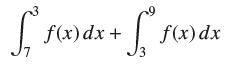
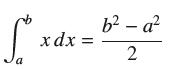
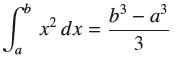
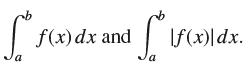
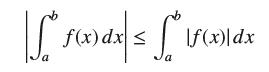
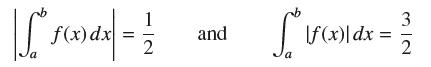
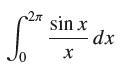
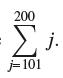
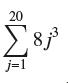
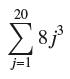
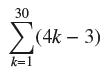
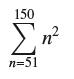
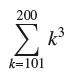
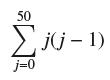
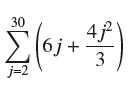
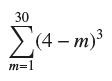
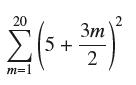
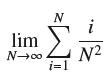
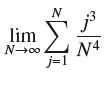
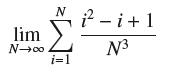
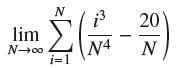
![lim RN, f(x) = 3x + 6, [1,4] N0](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/2/9/3/15165586a1fca7471700293153382.jpg)
![lim Ly, f(x)=x+2, [0,4] N0](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/2/9/3/16365586a2be024c1700293166825.jpg)
![lim Ly, f(x) = 4x-2, [1,3] N0](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/2/9/3/23965586a778ac9c1700293242375.jpg)