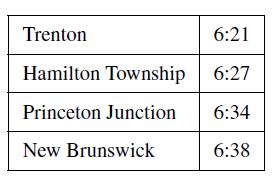
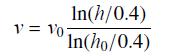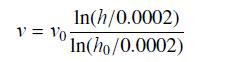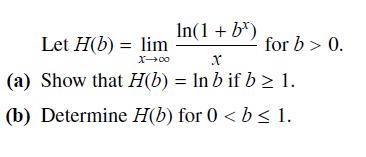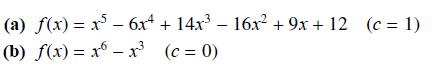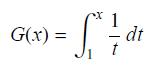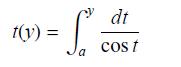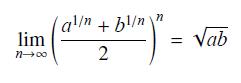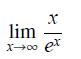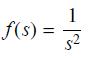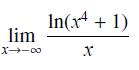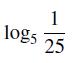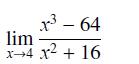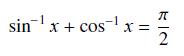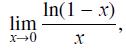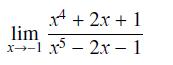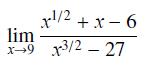![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


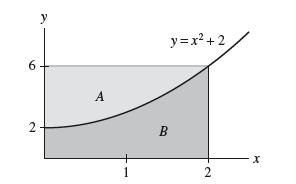
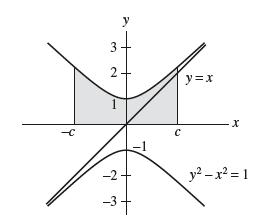
![f(x) = sec x, []](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/7/2/9/296655f11d019ef91700729296492.jpg)
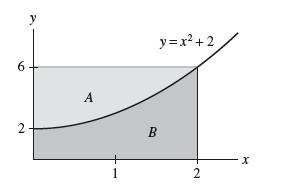
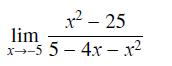
![THEOREM 1 The Mean Value Theorem Assume that f is continuous on the closed interval [a, b] and differentiable](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1701/0/3/6/6396563c25f4b15d1701036641858.jpg)