![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


![f(x) = 2x + x, [-2, 2]](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/2/9/6/0796558758fe0c0c1700296082665.jpg)
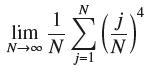
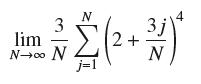
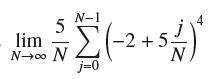
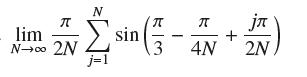
![RN, f(x)= x over [1,7]](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/2/9/7/0666558796a0d1a31700297068951.jpg)
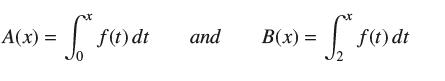
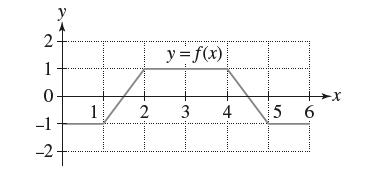
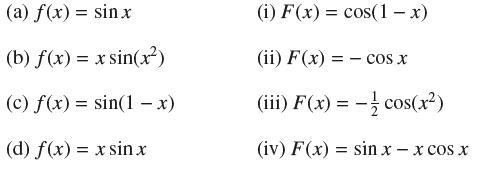
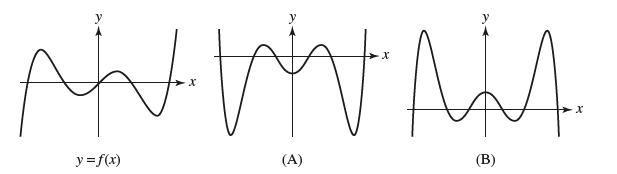
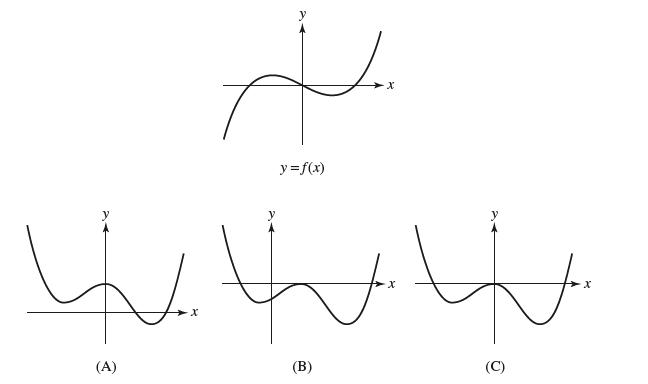
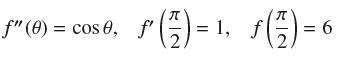
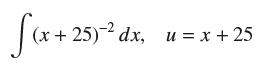
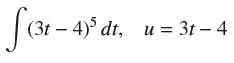
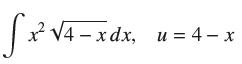
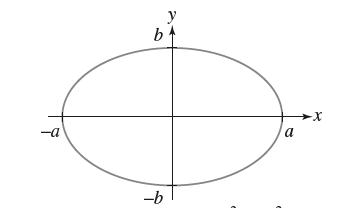
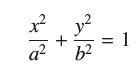
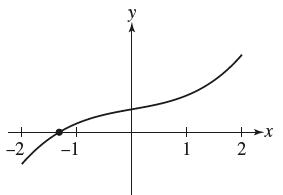
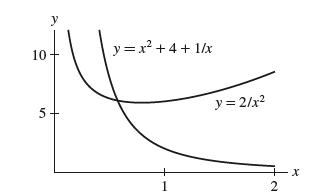
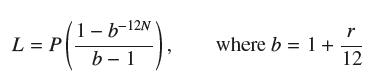
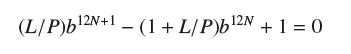
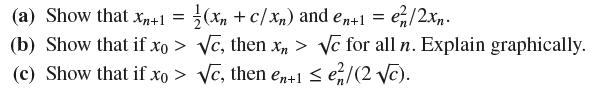
![y = X x+2' [1,4]](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1699/7/0/4/267654f6dcbd8d571699704267331.jpg)
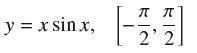
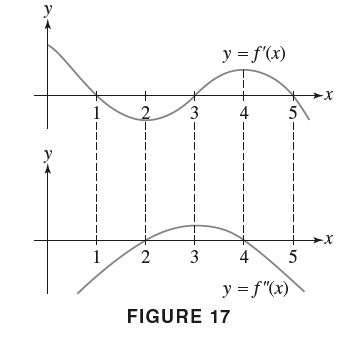
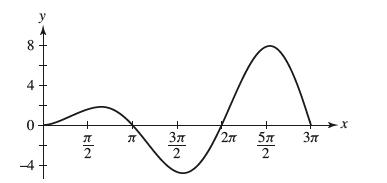
![EXAMPLE 4 Investigate the behavior of f(x) = cos x + cos x + x over [0, 7], and sketch its graph.](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1699/8/7/3/865655204492dd0b1699873865480.jpg)
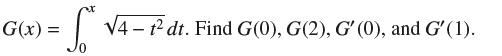
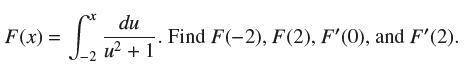
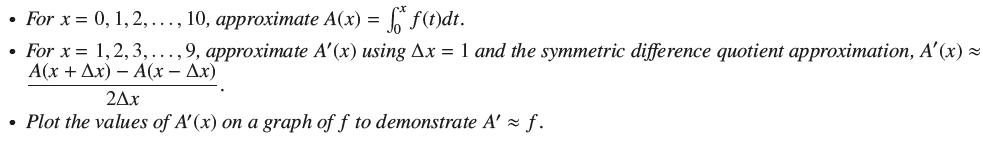
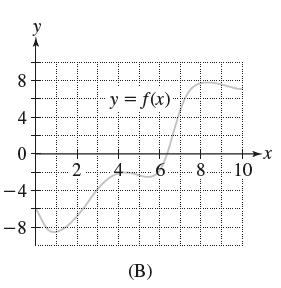
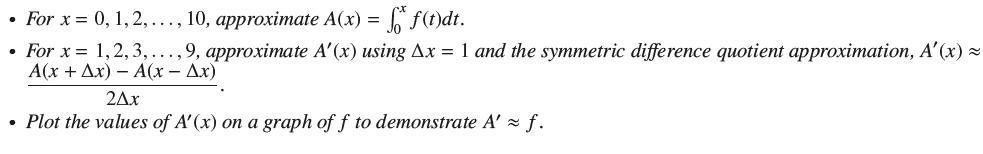
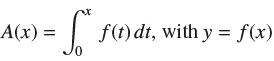
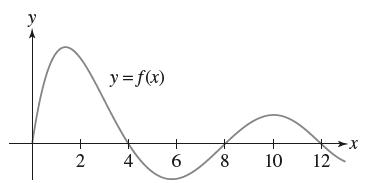
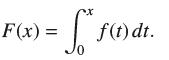
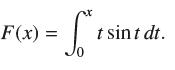
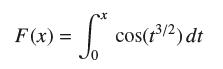

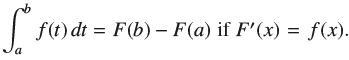
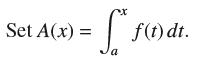
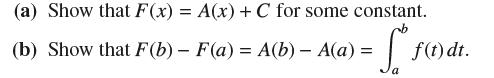

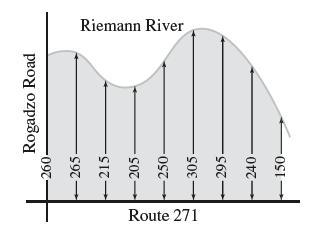
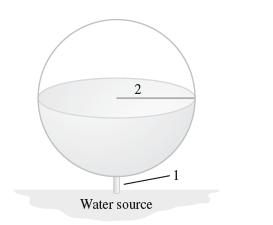
![f(x) = sin(/x) x [1, 2]](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/7/2/9/359655f120fe75d11700729360399.jpg)