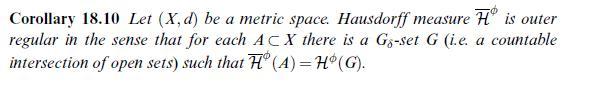![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()








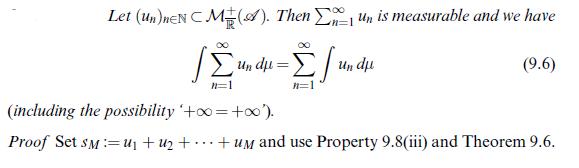








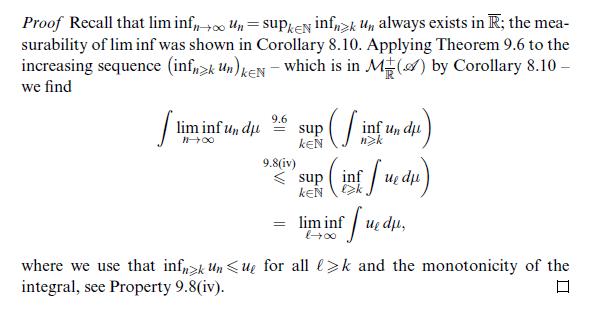

![Cantor's ternary set. Let (X, )= ([0, 1], [0, 1] (R)), A=A [0,1], and set Co= [0, 1]. Remove the open middle](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/6/6/0/59265aa50b0074b21705660591454.jpg)
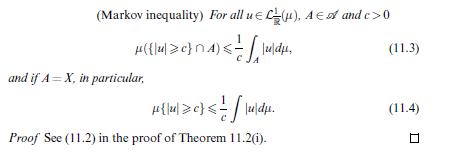




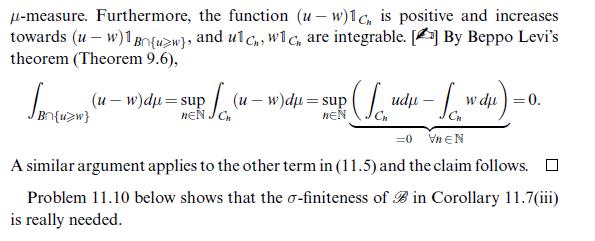


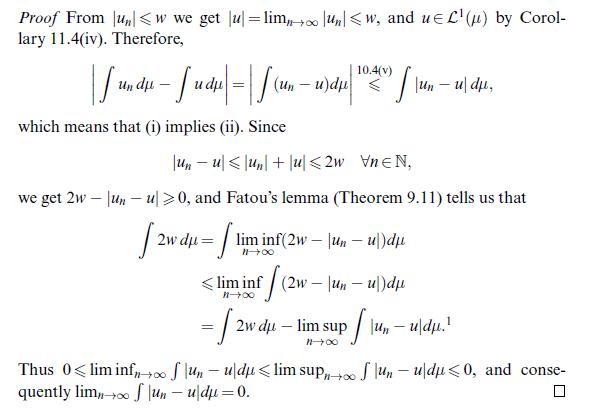
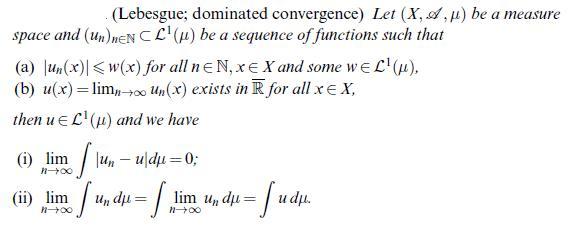
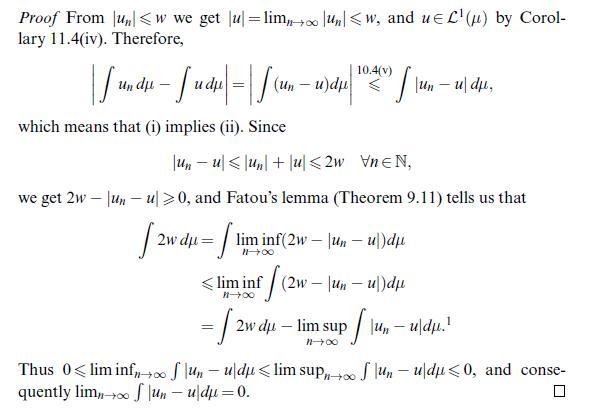
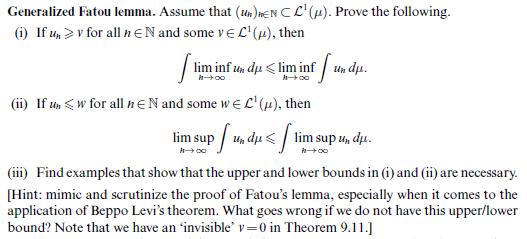
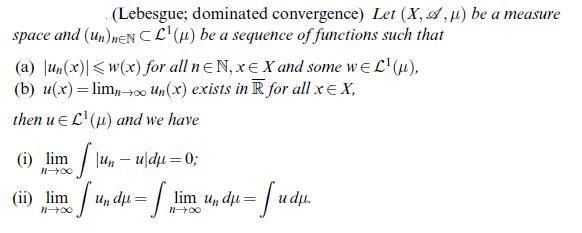
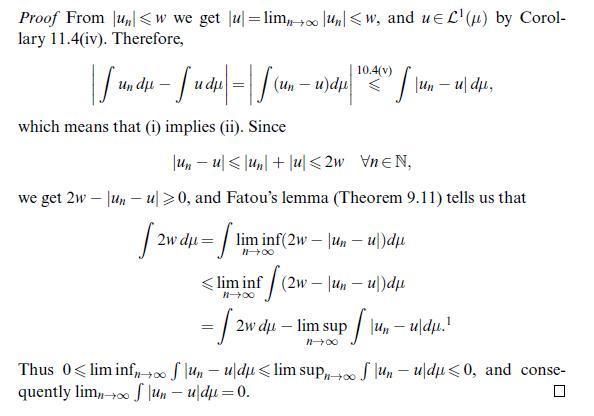
![Let (un)neN CM(A). Then 1 un is measurable and we have undu= |undu | n=] (including the possibility too =](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/7/2/4/19565ab4923ef7a51705724195415.jpg)
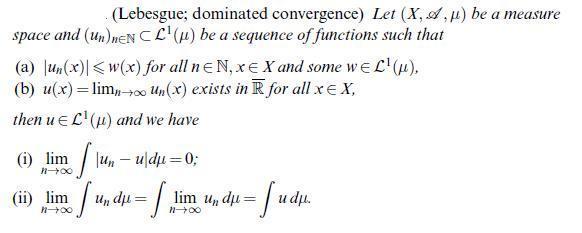
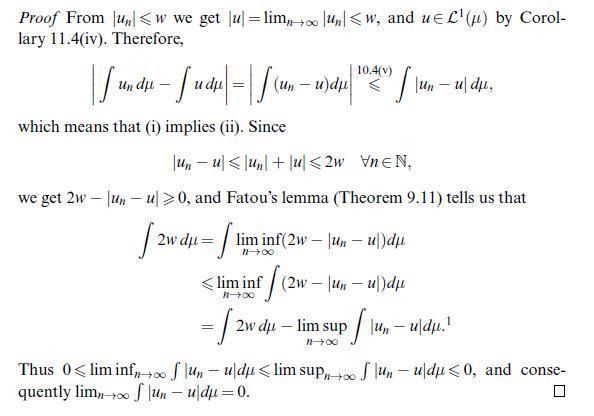


![(v) A={ACX: #A < #Nor #A < #N] is a o-algebra. Proof: Let us verify () (3). (): X = 0), which is certainly](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/5/7/9/94365a915a70af811705579942685.jpg)
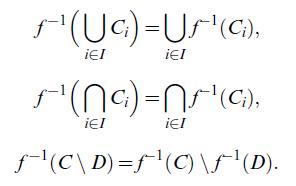


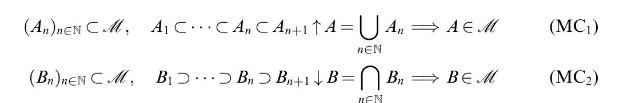
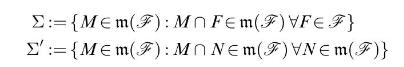












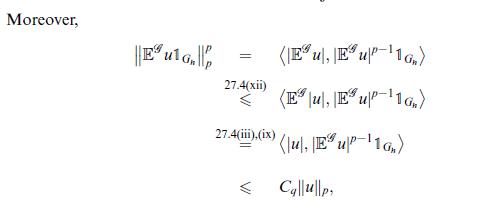



![(Carathodory) Let SCP(X) be a semi-ring and u: 8 [0,00] a pre-measure, i.e. a set function with (1) (0)=0;](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/6/3/5/77665a9efc09ea331705635776402.jpg)
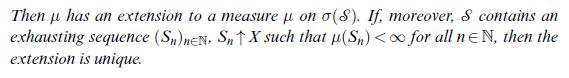
![Theorem 28.6 (Weierstra) Polynomials are dense in C[0,1] w.r.t. uniform convergence. Proof (S. N. Bernstein)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/8/9/7/86265adef86c7d601705897860666.jpg)

![Consider the open [] sets U:= {xe X: d(x, Fi)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/9/0/3/62165ae0605d8c8c1705903621569.jpg)