![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


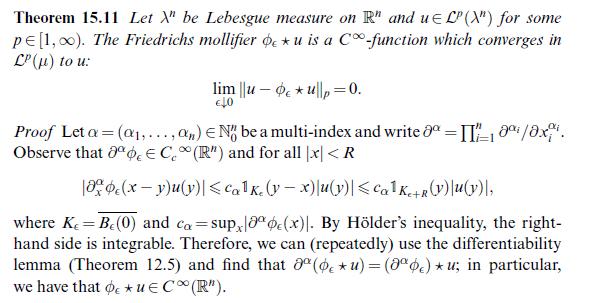

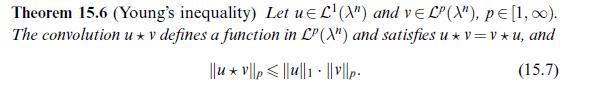

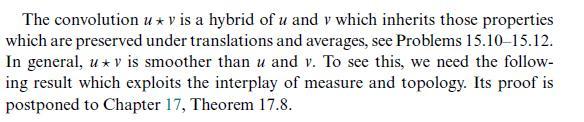
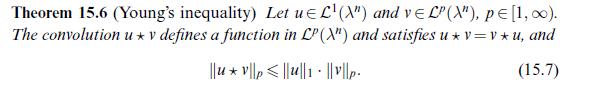





![Corollary 16.14 Let :R" a (0,1]. If ad>n, then B(Rd), and the inequality Rd be an a-Hlder continuous map](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/7/5/3/91565abbd3bd30e61705753913560.jpg)




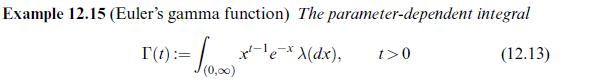



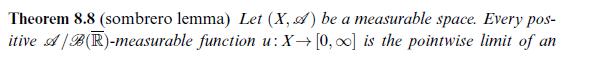




![Theorem 28.6 (Weierstra) Polynomials are dense in C[0, 1] w.r.t. uniform convergence. Proof (S. N. Bernstein)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/8/9/7/92465adefc4982a11705897922446.jpg)
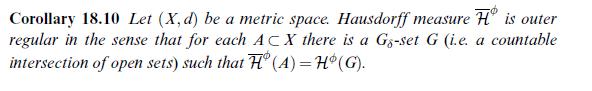


![It is a simple exercise to show that (R") are indeed the H-measurable sets. [] (ii) By Theorem 18.7 (R) C*.](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/9/0/3/88465ae070c078281705903883440.jpg)






![A (positive) measure on X is a map : [0, ] satisfying A is a o-algebra in X, (0) = 0, (An) nEN CA pairwise](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/5/8/3/70965a9245d135e31705583708964.jpg)

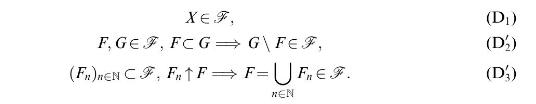



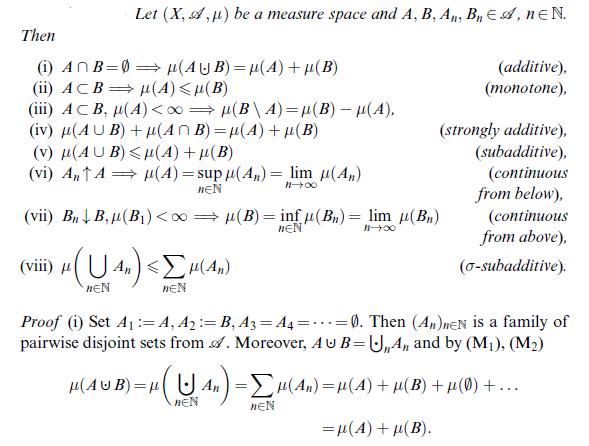
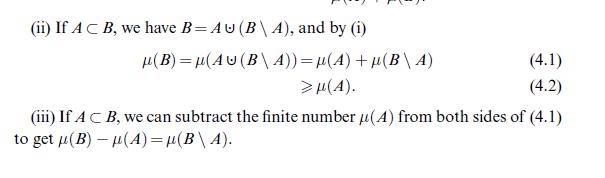

![(Carathodory) Let SCP(X) be a semi-ring and u: S [0, ] a pre-measure, i.e. a set function with (i) (0)=0;](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/6/3/6/76765a9f39f8b5491705636767323.jpg)
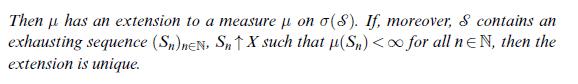
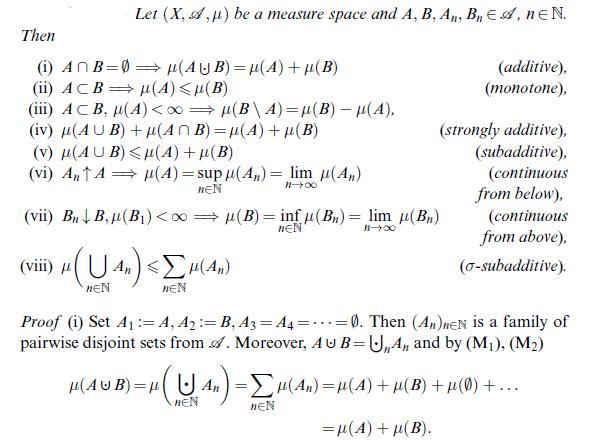
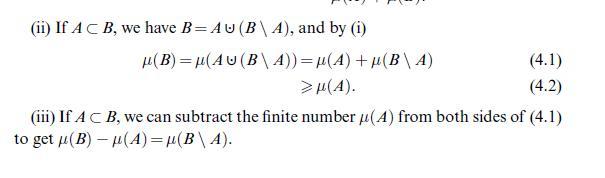

![(Carathodory) Let 8C P(X) be a semi-ring and u: S [0, ] a pre-measure, i.e. a set function with (i) (0) = 0;](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/6/3/6/85265a9f3f4d614e1705636852299.jpg)
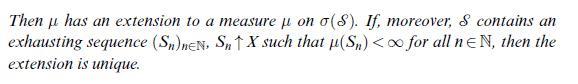
![(Carathodory) Let S P(X) be a semi-ring and u: S [0, ] a pre-measure, i.e. a set function with (i) (0) = 0;](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/6/3/6/88565a9f415b01bd1705636885415.jpg)
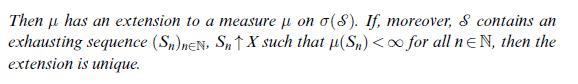







![(sombrero lemma) Let (X, A) be a measurable space. Every pos- itive A/B(R)-measurable function u: X [0,0] is](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/6/4/4/80565aa1305d55ef1705644805186.jpg)

![(sombrero lemma) Let (X, A) be a measurable space. Every pos- itive A/B(R)-measurable function u: X [0, ] is](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/6/4/5/18165aa147d9271c1705645181042.jpg)
