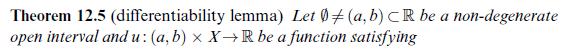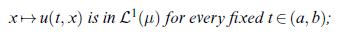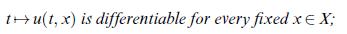![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()




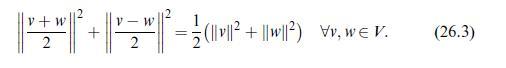

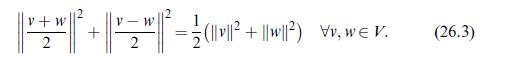

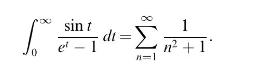
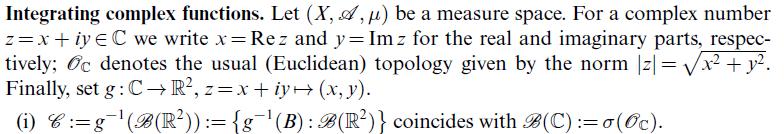
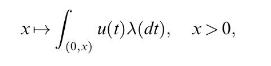
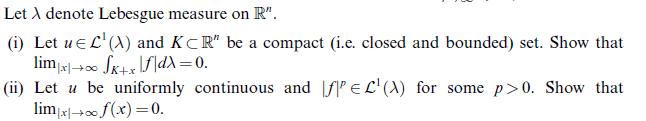
![(mean value theorem for integrals) Let u R[a, b] be either positive or negative and let ve C[a, b]. Then](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/7/2/5/11465ab4cba5fb8a1705725113837.jpg)

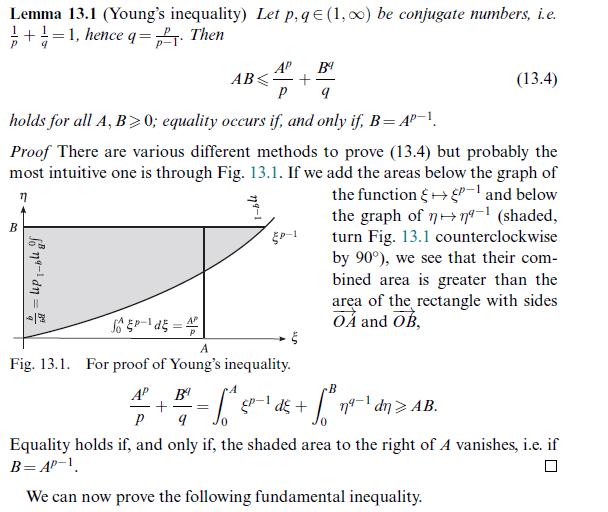


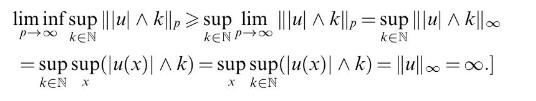
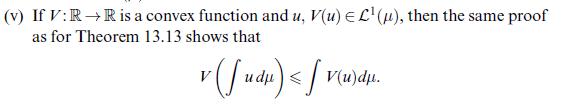
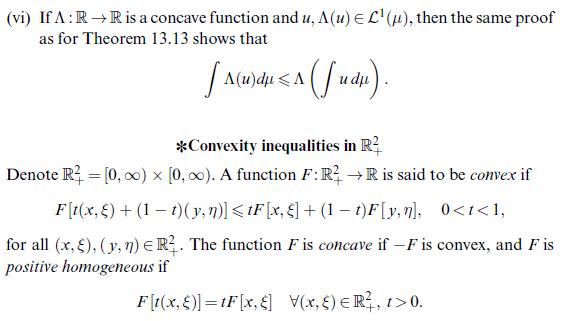
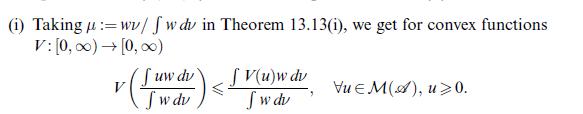
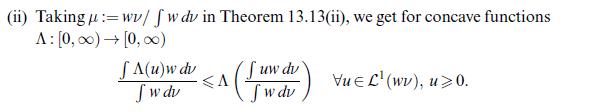
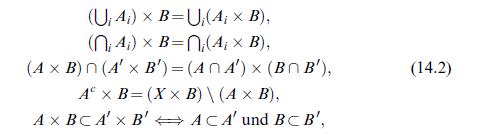
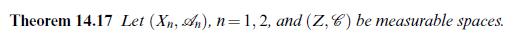
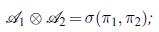
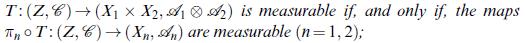
![if x > 0, if x = 0, -(x, 0], if x <0, (0, x], F(x):= 0, and G(x):= if x > 0, if x=0, -v(x, 0], if x <0, v(0,](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/7/3/9/38265ab847695cab1705739381868.jpg)
![o(F(b)) (F(a)) = ['(F(s-))dF(s) + [(F(s)) (F(s-)) 6'(F(s))AF(s)]. - a](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/7/3/9/47765ab84d5a1e491705739476905.jpg)