![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


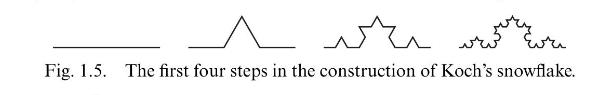


![approximating sequence [2]!) and defines an element Fu= L(X"); the identity (19.14) remains valid since the](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/9/0/5/58565ae0db1a07bd1705905580843.jpg)