![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


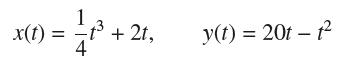
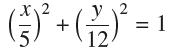
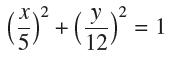
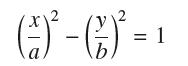
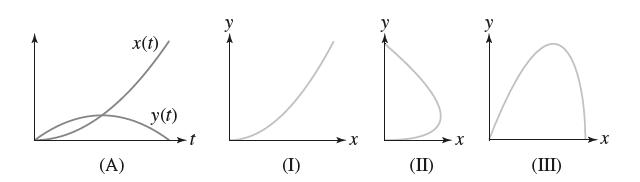
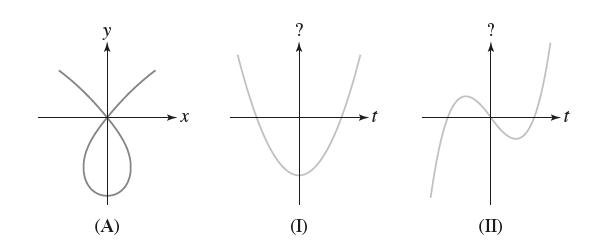
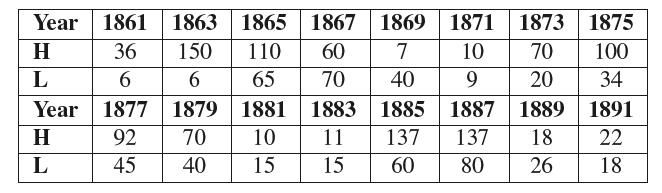
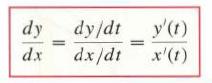
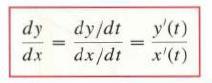
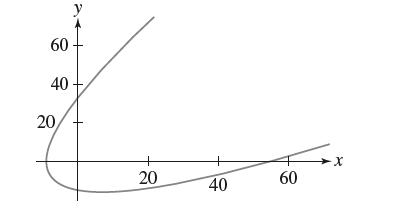
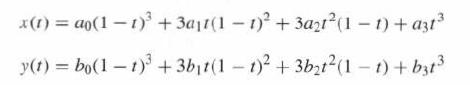

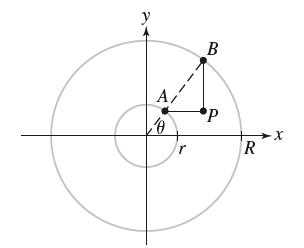
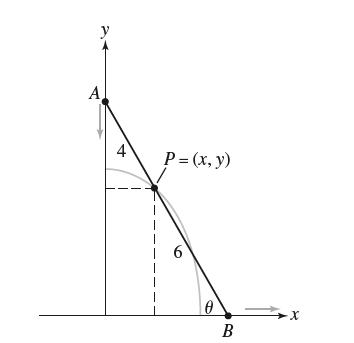

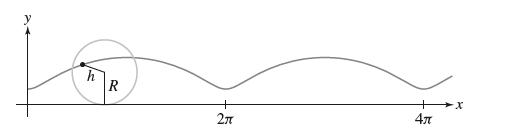
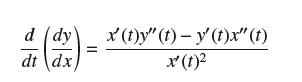
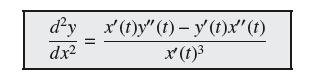

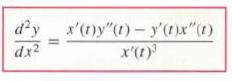

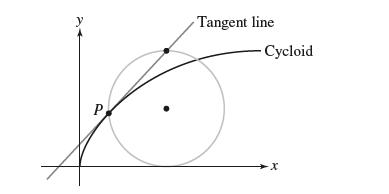
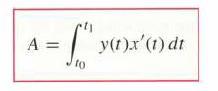
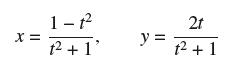
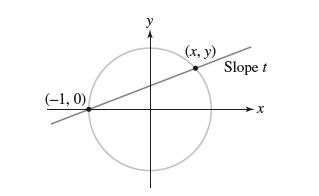
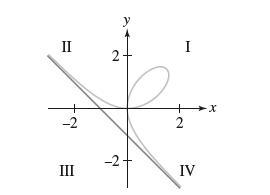
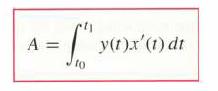
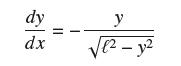
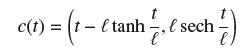
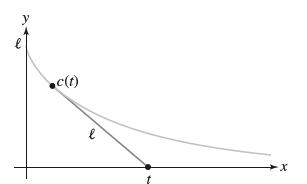
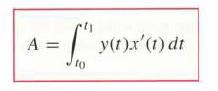
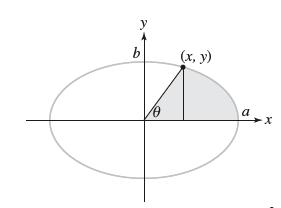
![- Sbs S = b sinu a sinu du = ab Sinudu 1 Sc (2-3cos 24) du = ab | 2 - Sin24] 16 2ut = ab = ab |- - -sin2t_0=](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1703/0/5/5/588658290e4e05311703055588397.jpg)