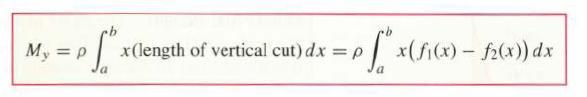![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


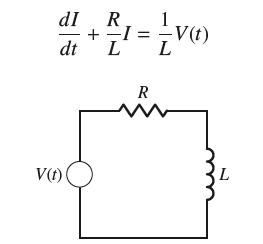
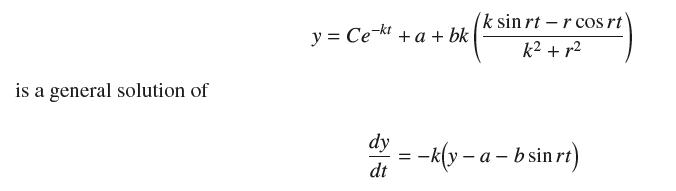


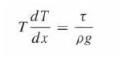
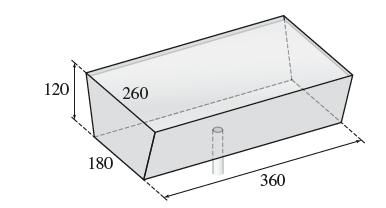
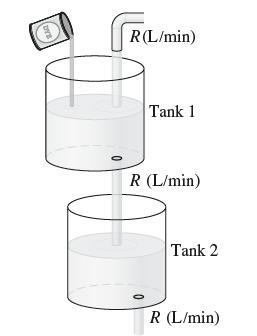
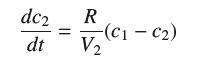
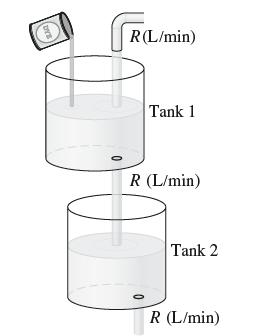
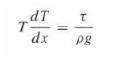
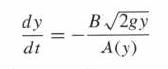
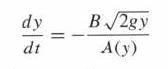
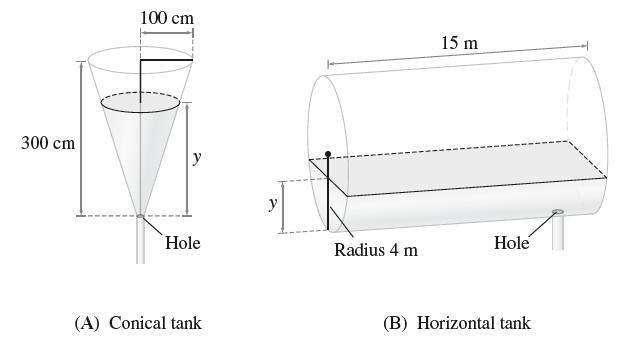
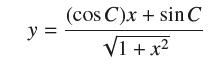
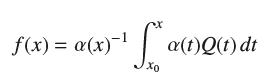
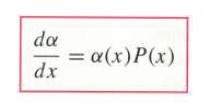
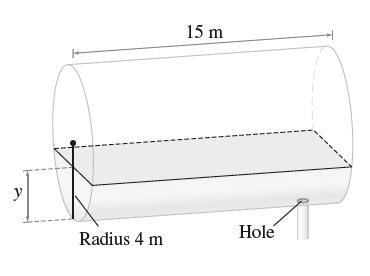
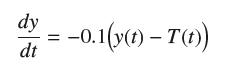
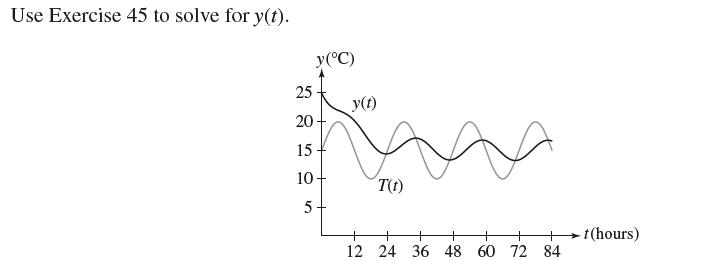
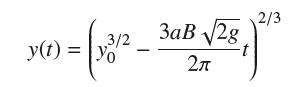
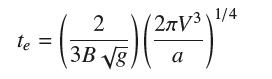
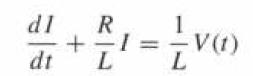
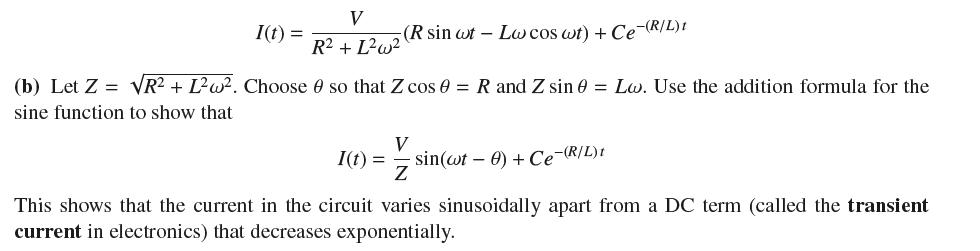
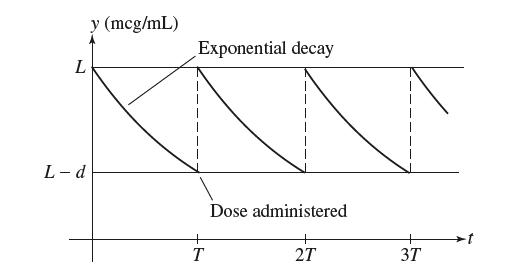
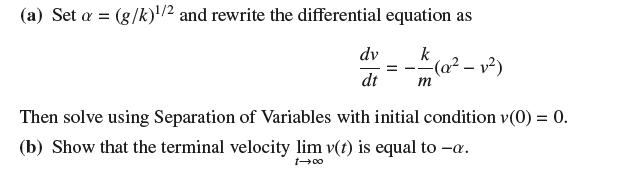
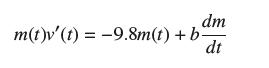
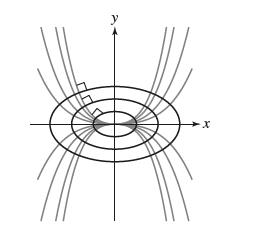
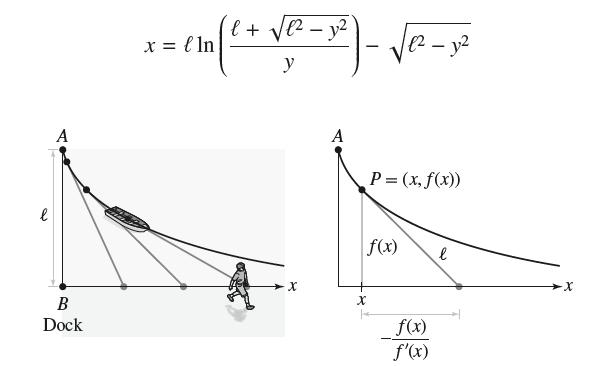
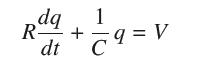
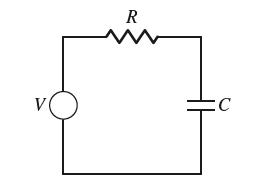

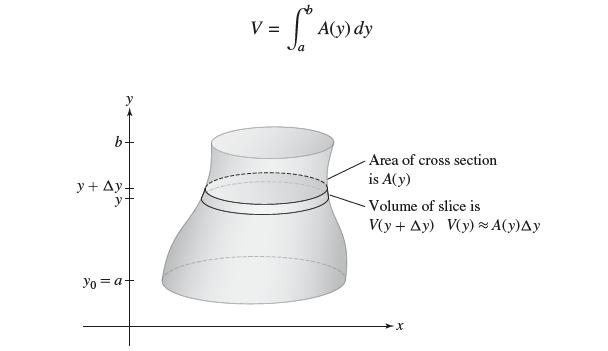
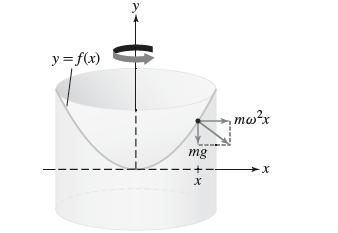
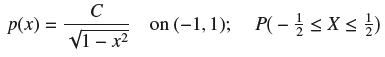
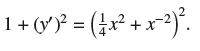
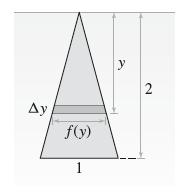
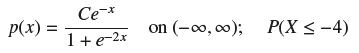
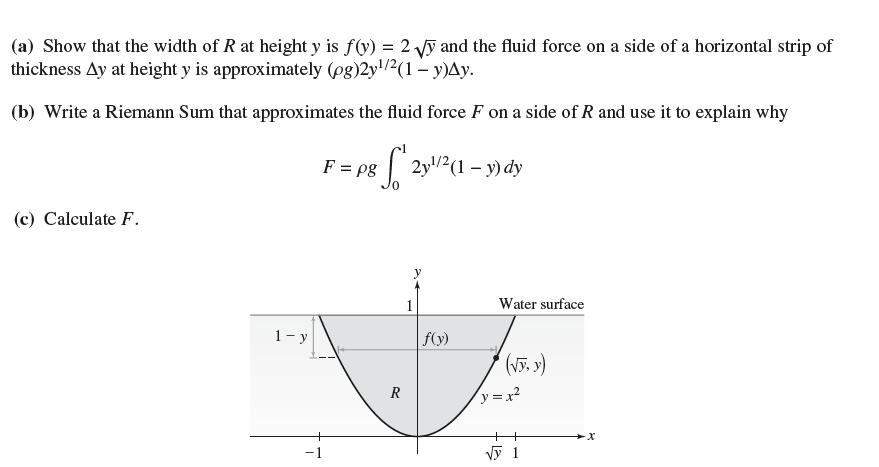
![y = X 1 + over [1,4]. 2x](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1702/0/3/7/940657309b468a541702037938982.jpg)
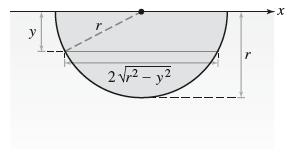
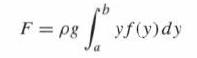
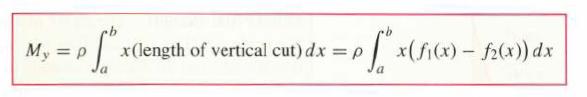

![y = 10 + -3 X 6 [1,2]](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1702/1/9/8/42665757c9ad70e91702198426340.jpg)