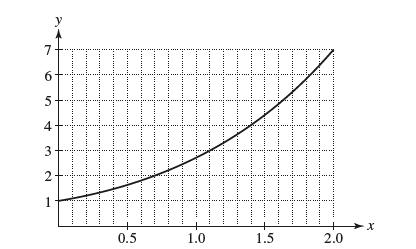
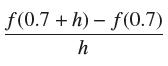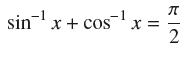![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


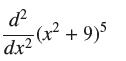
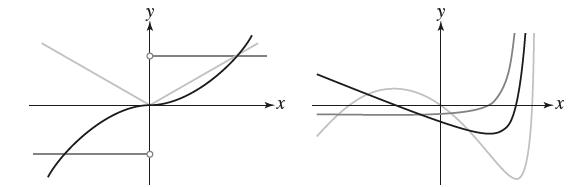
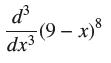
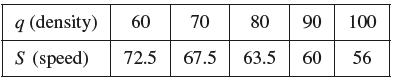
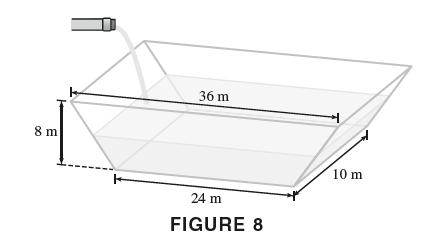
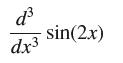

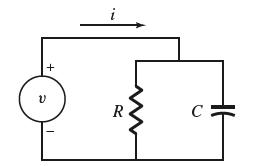

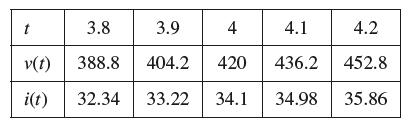
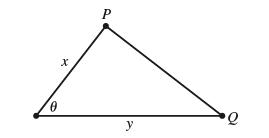
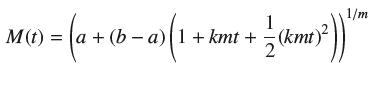
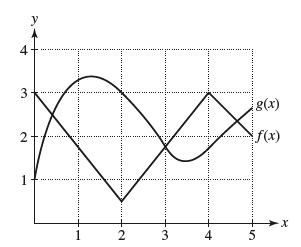
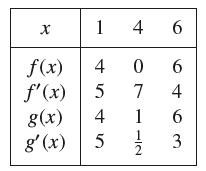
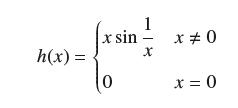
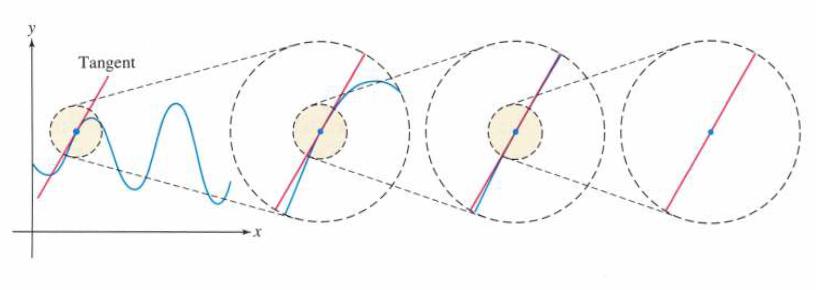
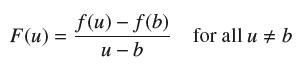
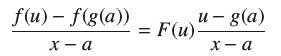
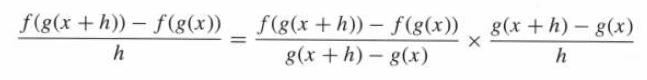
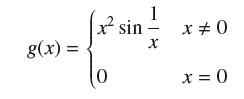
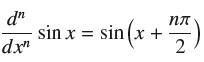

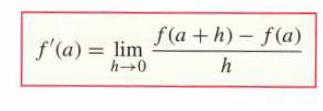
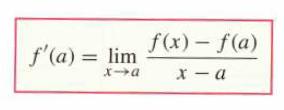
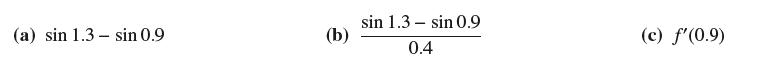
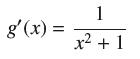

![(a) Assume that g and h are continuous on [a, b]. Use Corollary 2 to show that if g(a)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1698/5/8/8/187653e661b7f3221698588186969.jpg)