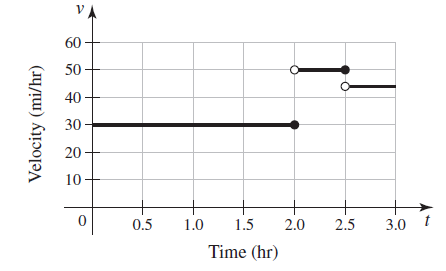
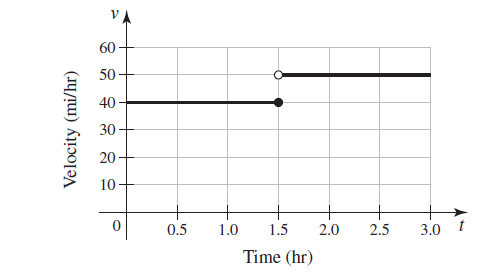
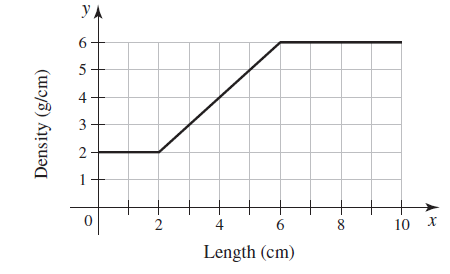
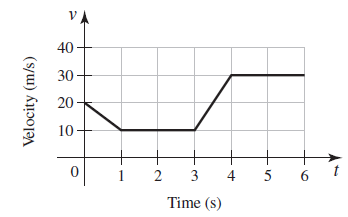
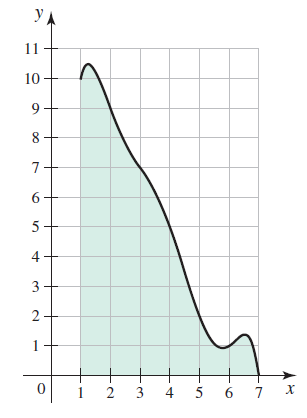
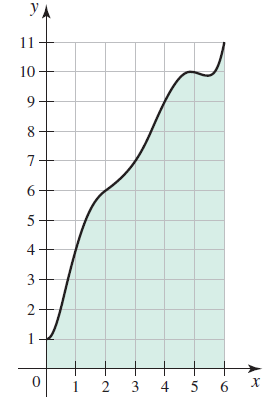
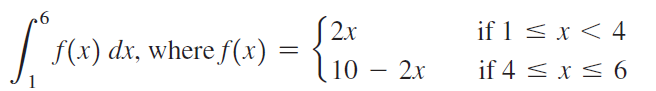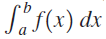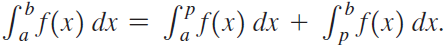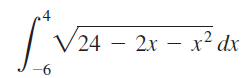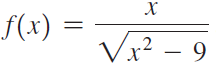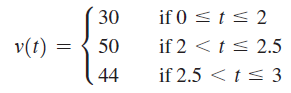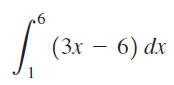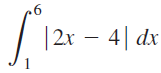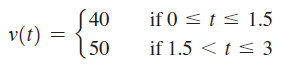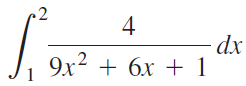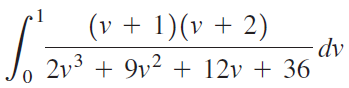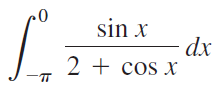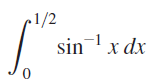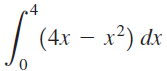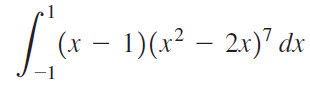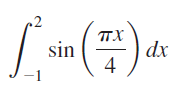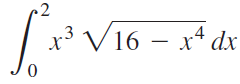![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


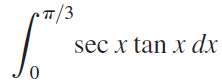
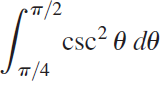
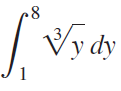
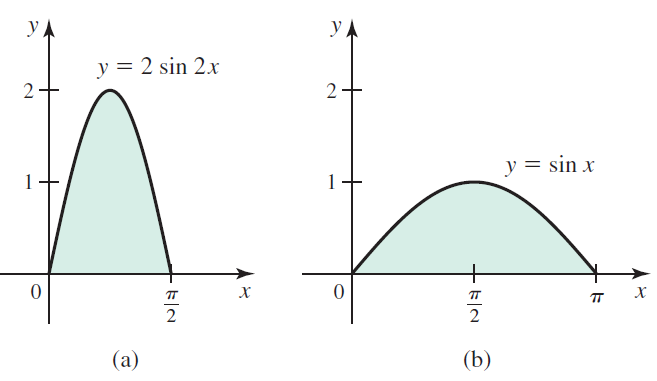
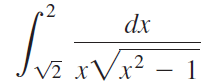
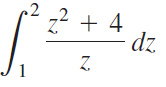
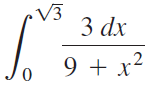
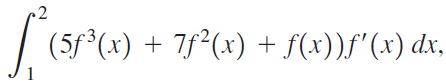
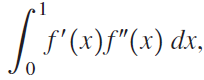
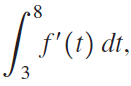
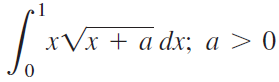
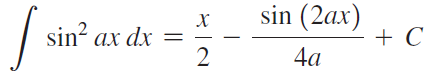
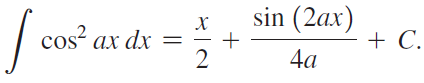
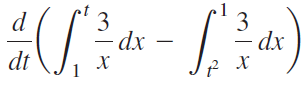
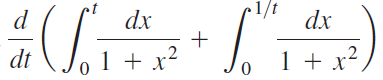
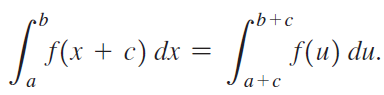
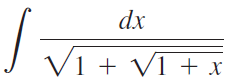
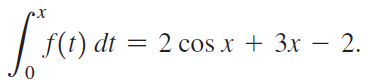
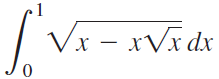
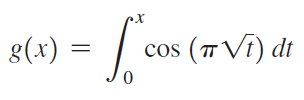
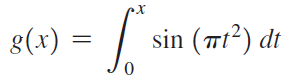
![Decreasing on [a, b] [a,b] Concave up on [a,b] [a, b] Concave down on](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1551/2/6/2/9075c7664bb1ec591551245650601.jpg)
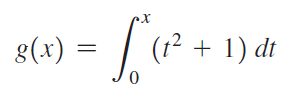
![Increasing on [a,b] Decreasing on [a, b] Concave up on [a,b] [a, b] Concave down on](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1551/2/6/2/8345c766472885ba1551245577977.jpg)
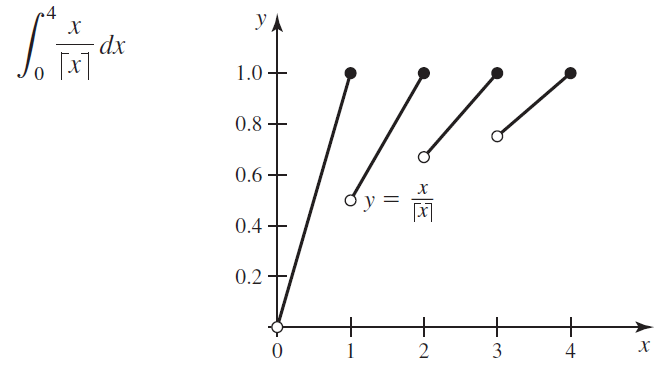
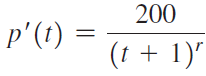
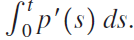
![•5 УА x [x] dx 15 - y = x[x] 10 5 + + + х 3 4](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1551/2/8/2/9085c76b2dc405001551265651022.jpg)