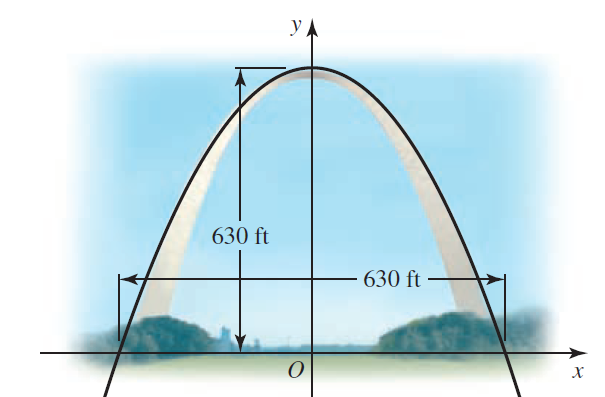
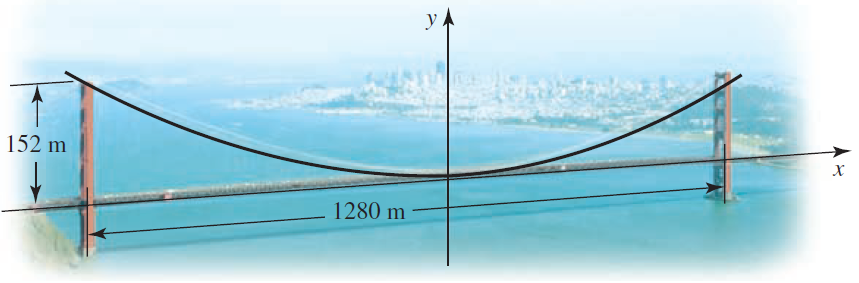
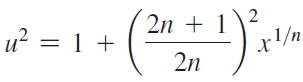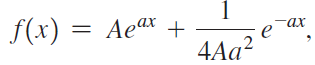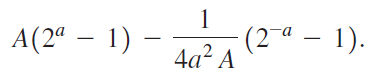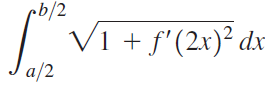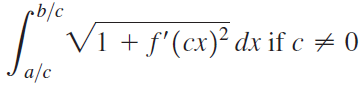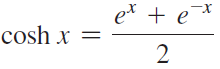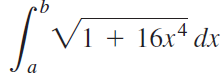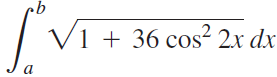![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


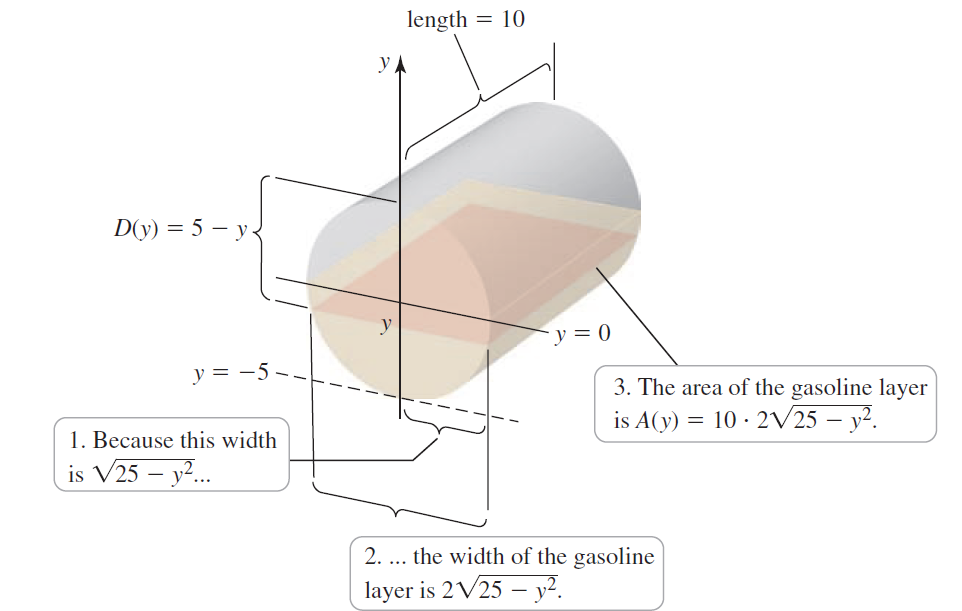
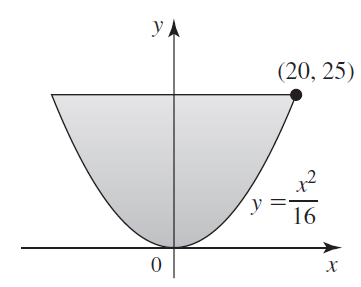
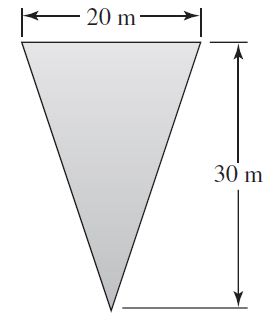
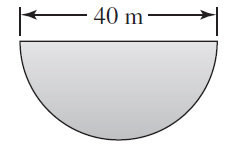
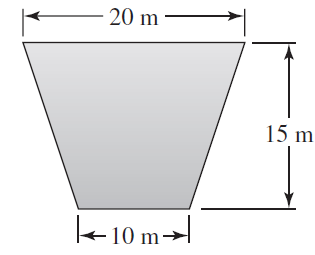
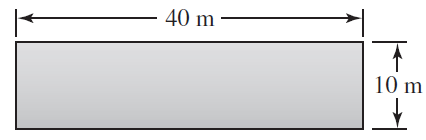
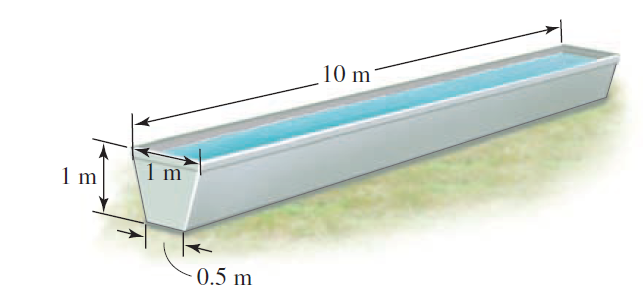
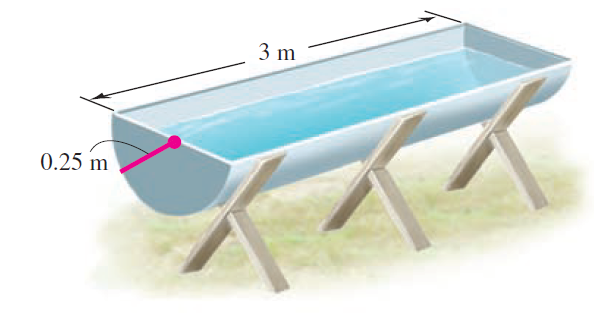
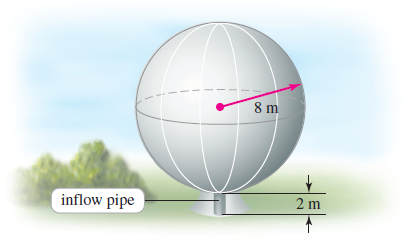
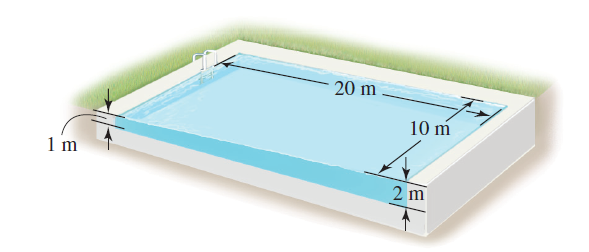
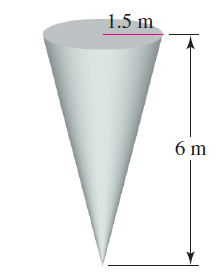
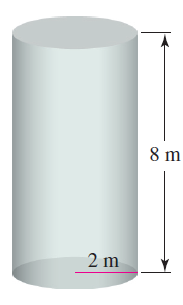
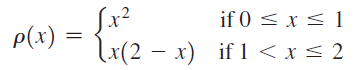
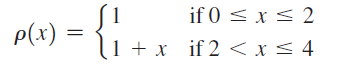
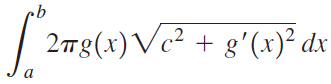
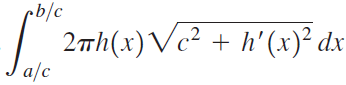
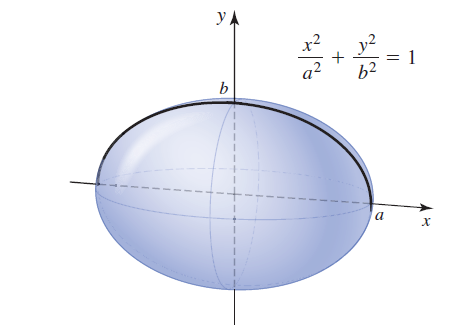
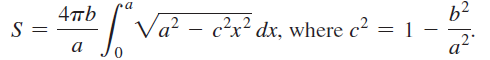
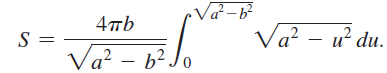
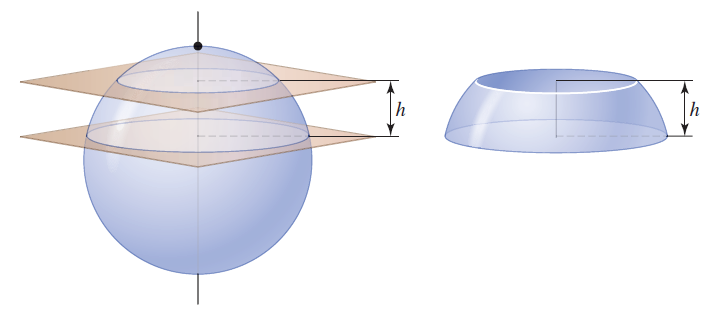
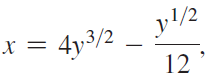
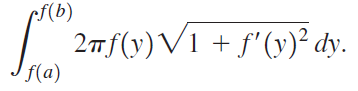
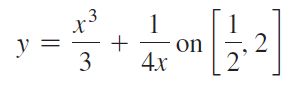
![x4 on [1, 2] 4x2](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1551/7/2/0/1635c7d5ee3b580e1551702892214.jpg)
![Не* + e 2) on [-2. 2] -2х](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1551/7/2/0/1465c7d5ed2702c71551702874848.jpg)
![x/2 y = x3/2 on [1, 2] 3](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1551/7/1/9/8275c7d5d930f0311551702555541.jpg)