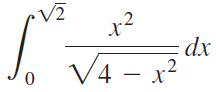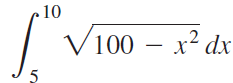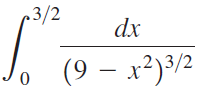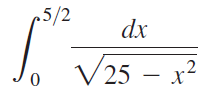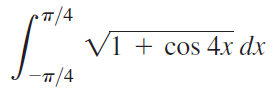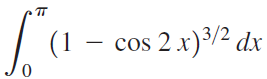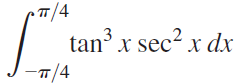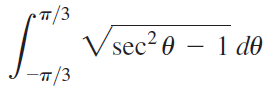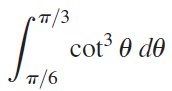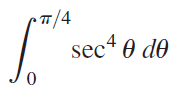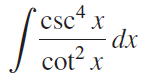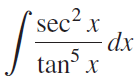![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


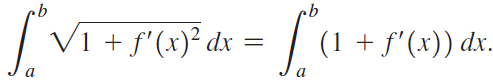
![y = V1 + f'(xr)? on [a, b].](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1551/7/1/5/3845c7d4c38705ed1551698112978.jpg)
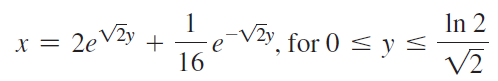
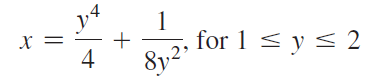
![on [-5, 5] x? + 1](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1551/7/1/5/1015c7d4b1da447a1551697830204.jpg)
![1 on [1, 10] У х](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1551/7/1/5/0795c7d4b07d3a181551697808394.jpg)
![[1,4] on .2 х](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1551/7/1/5/0025c7d4aba3886e1551697730759.jpg)
![.3 х on [-1, 1] 3 ||](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1551/7/1/4/9555c7d4a8b52f841551697683837.jpg)
![x1/2 on [1,9] 3 ||](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1551/7/1/4/7725c7d49d45666b1551697500886.jpg)
![1 x4 y = on [1, 2] 8x2](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1551/7/1/4/7525c7d49c034d011551697480778.jpg)
![+3/2 у з 3 on [4, 16]| ||](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1551/7/1/4/7145c7d499a456c71551697442831.jpg)
![(x² + 2)³/2 y : on [0, 1] 3 ||](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1551/7/1/4/6905c7d498265b441551697418937.jpg)
![on [1,6] 24 y = 3 ln x](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1551/7/1/4/6635c7d49672c0981551697391713.jpg)
![on [0, 60] -x3/2 y = 3](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1551/7/1/4/6235c7d493faab691551697352251.jpg)
![(e* + e *) on [-In 2, In 2] уз 2](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1551/7/1/4/6085c7d4930696c91551697336977.jpg)