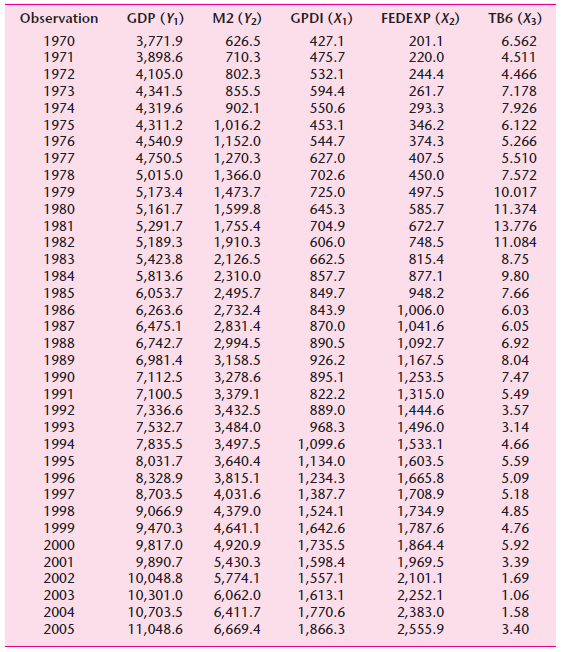
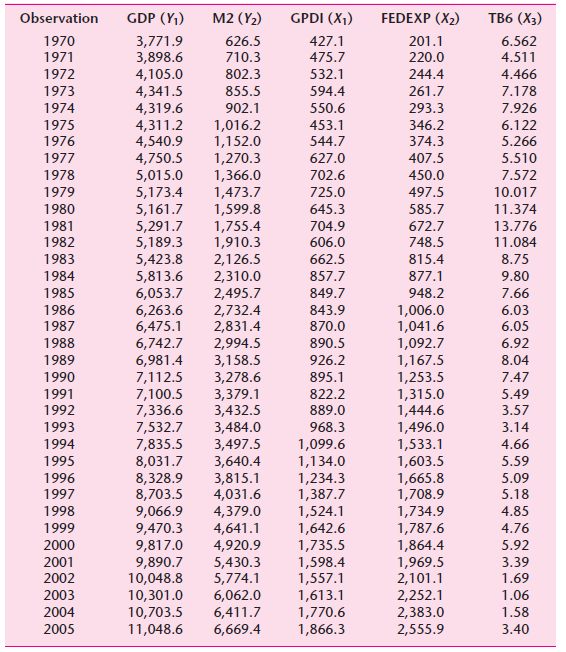
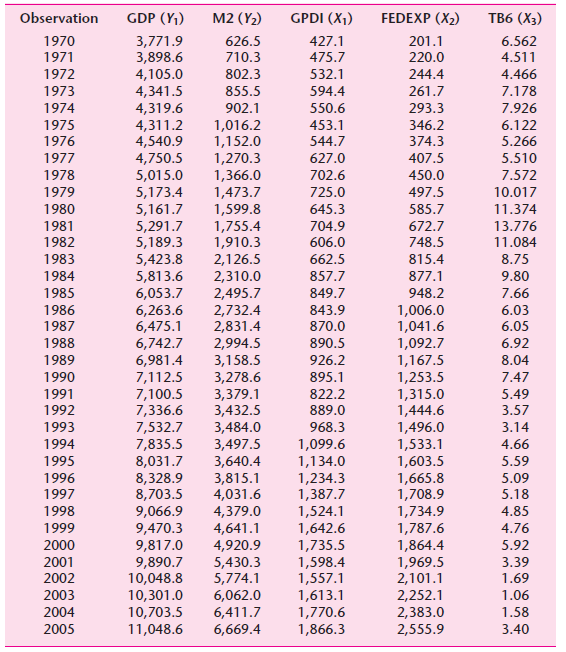
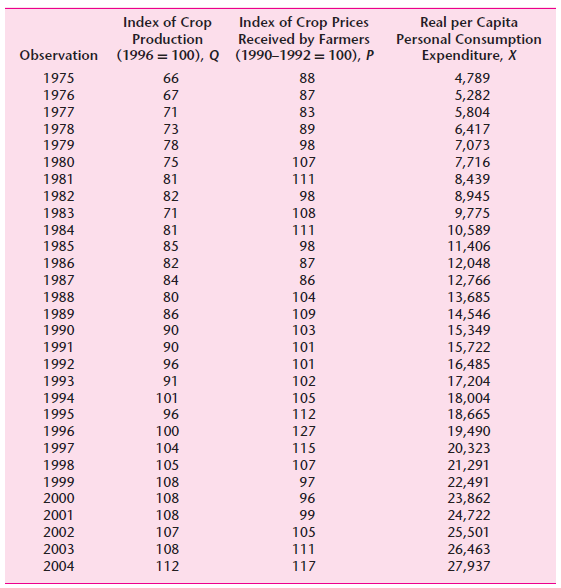
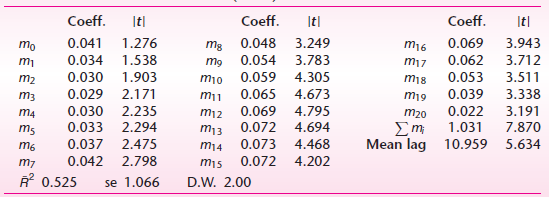
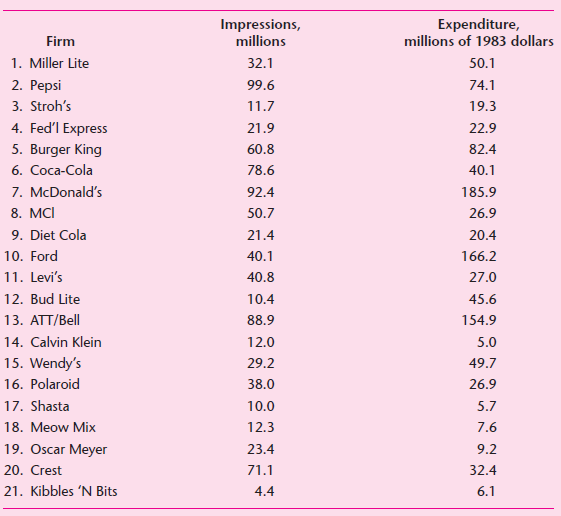
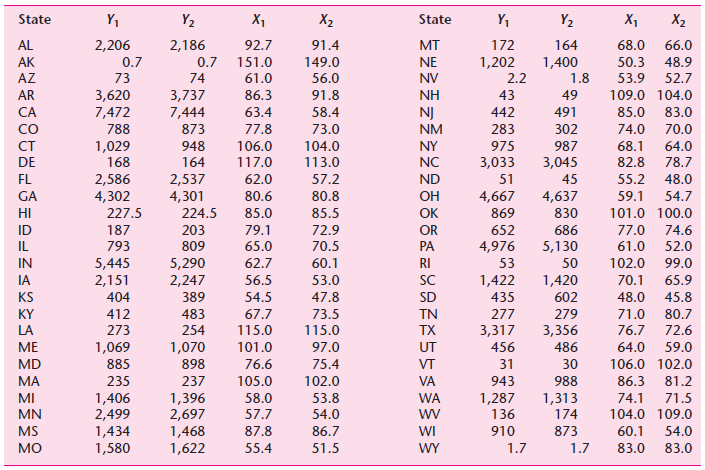
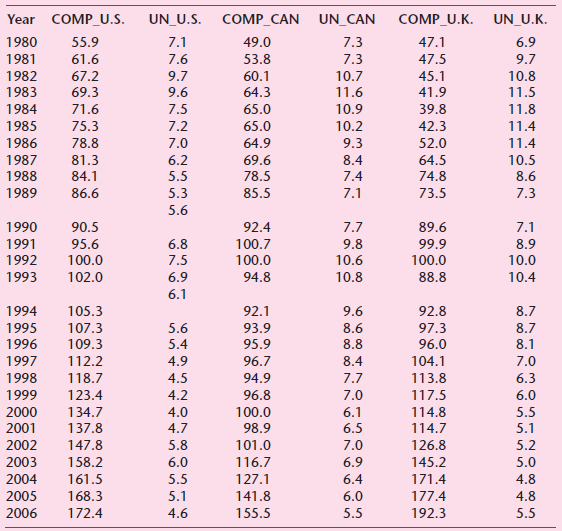
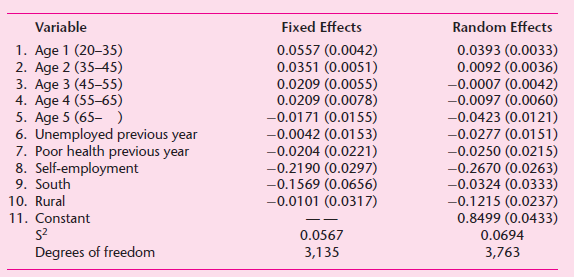
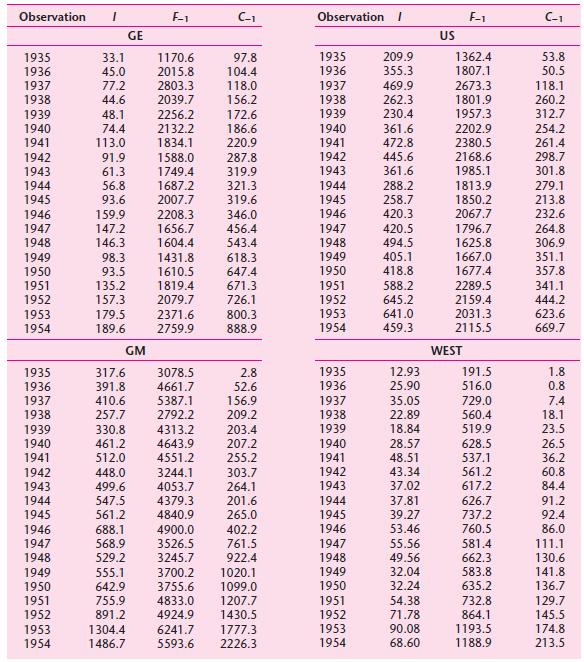
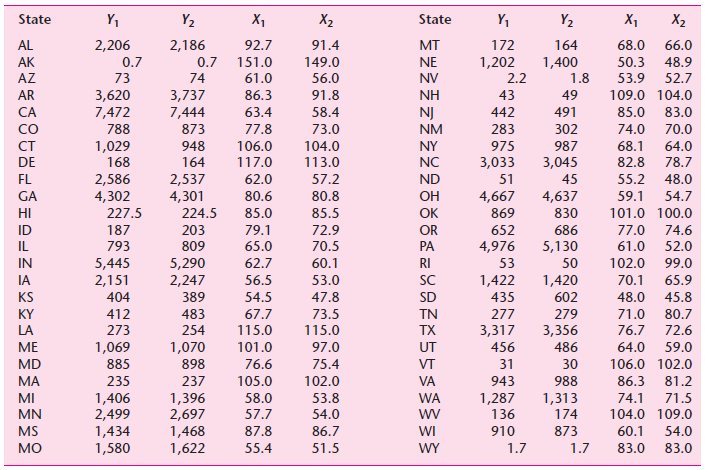
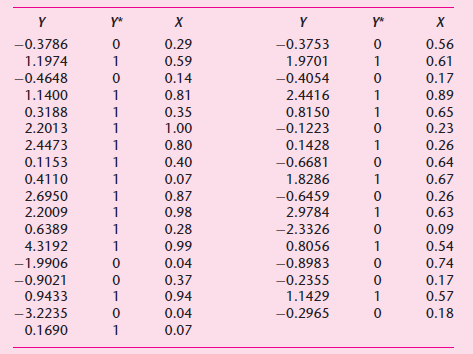
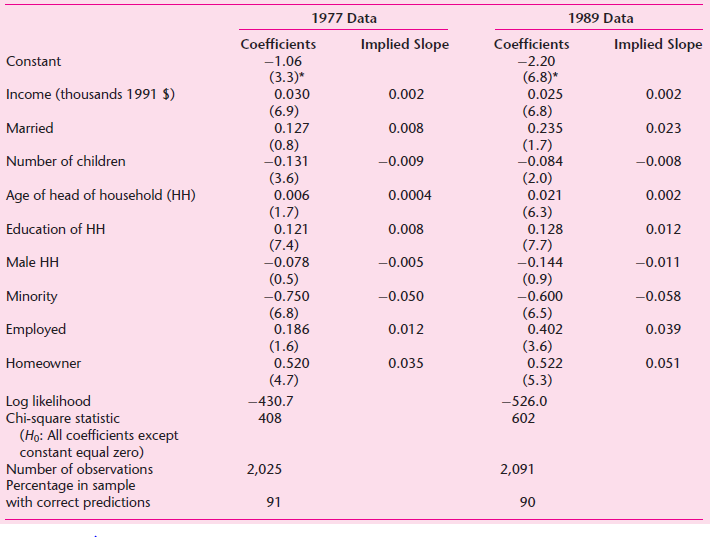
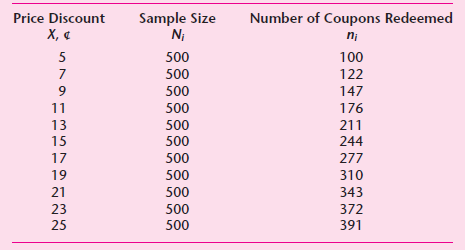
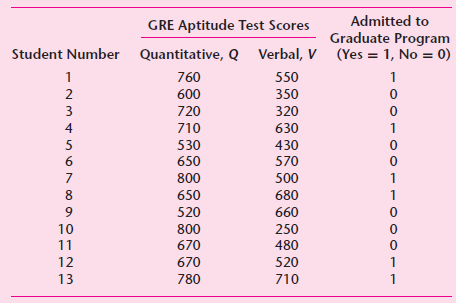
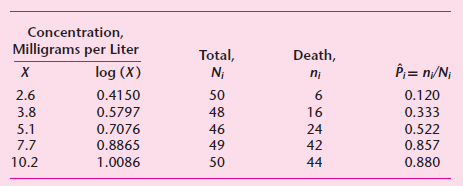
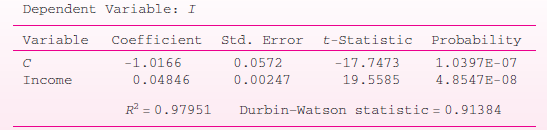
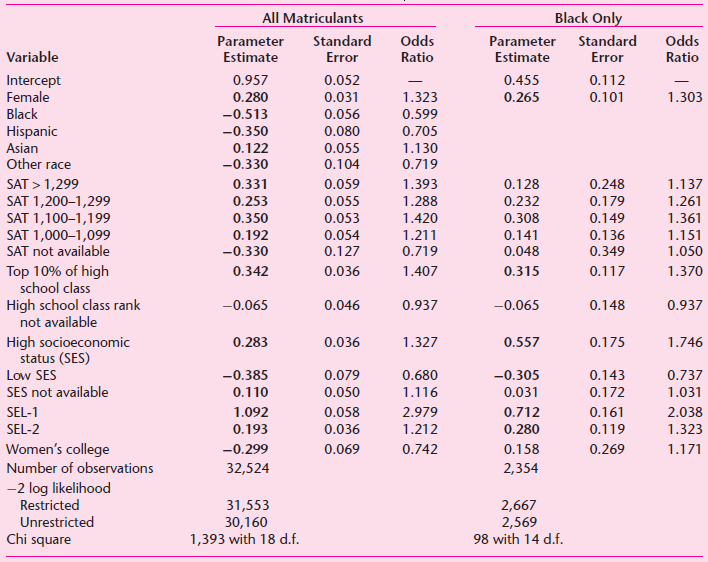
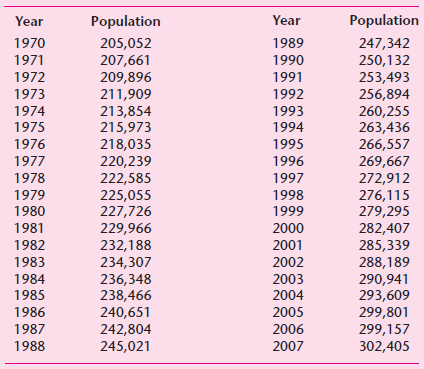
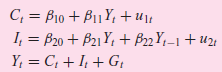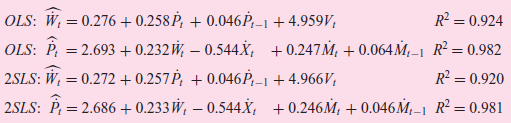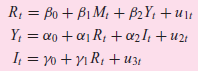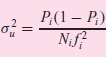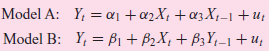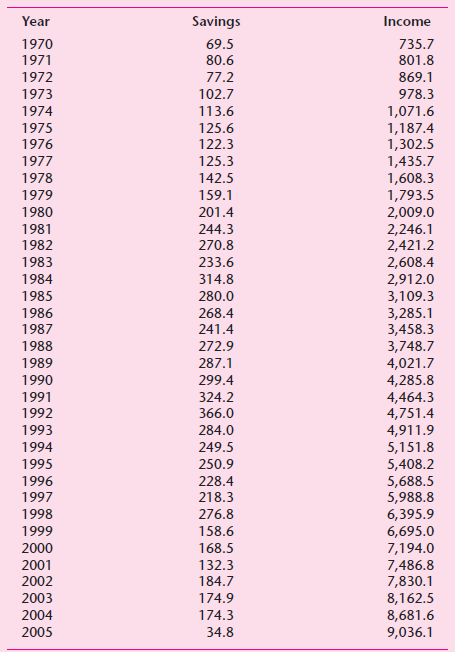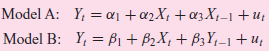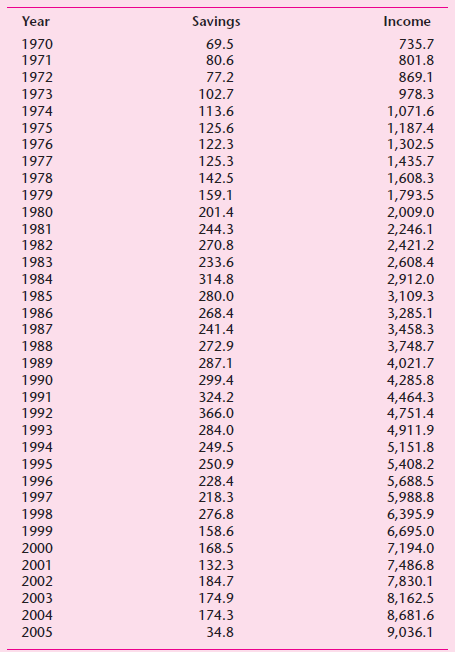![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


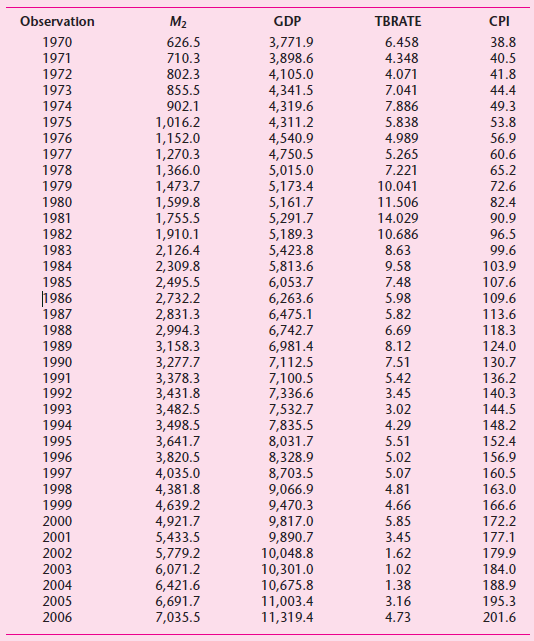
![Rht αι + α R + α3Rhr-1 + αL, + as + αςNIS, + α7] +ur RΒ +β) RH+ βRb,-1 + β,L+ β5Y+ β6NIS, + βΕ+ Lλ st](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1525/4/3/8/4385aec57e6d190c1525438423899.jpg)
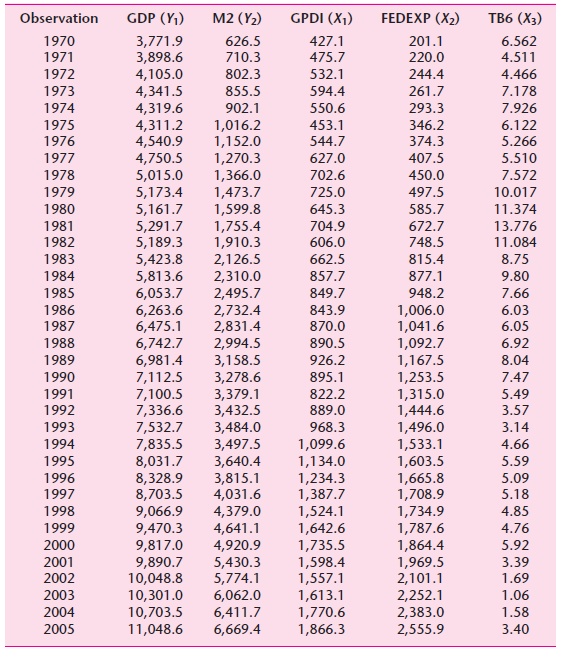
![|Yli = a1 + B1 Y2i + B2Y3¡ + B3Y4¡ + U ]i | Y2i = a2 + B4Y1; + B3 Ysi + yı X1i + y2X2i + u2i Y3i = a3 + B6 Y2i + Y3X3](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1525/4/3/8/4935aec581d9d2e31525438480954.jpg)
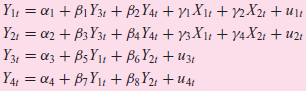
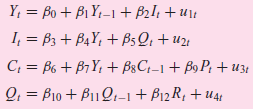
![Y; = C, + I; + G; C; = B1 + B2YD,–1+ B3M, + u]; I, = B4 + Bs(Y,-1 – Y;-2) + B6Z¡–1 + u2: G = B7 + BsG,-1+U31](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1525/4/3/8/6015aec5889c8e2a1525438588249.jpg)