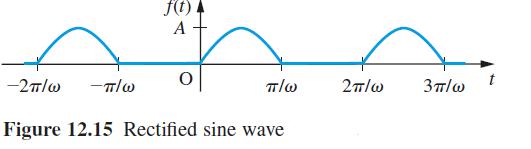
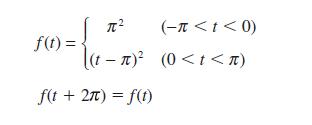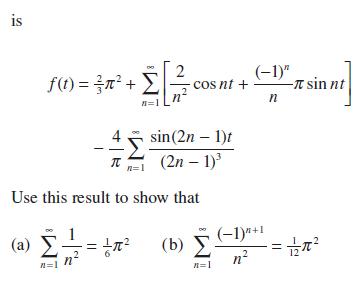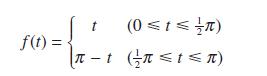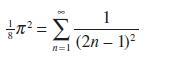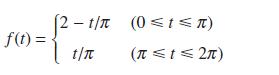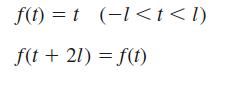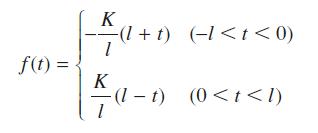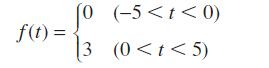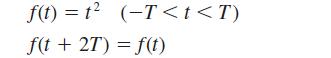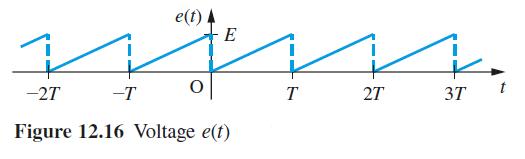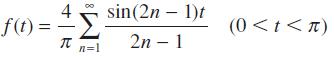![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()



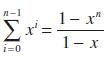
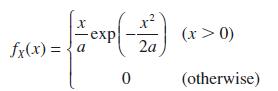
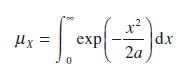
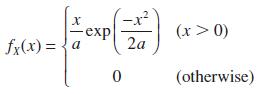

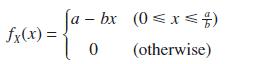



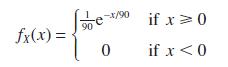
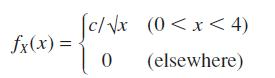
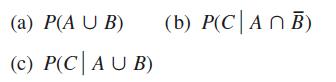


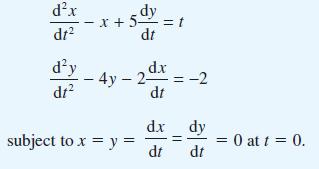
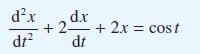
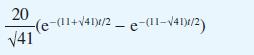
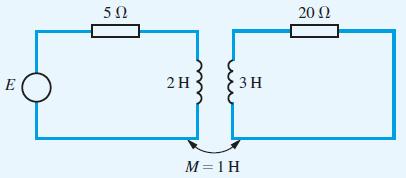
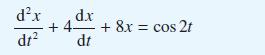
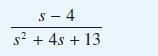
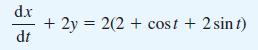
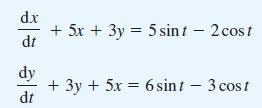
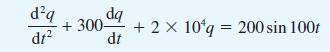
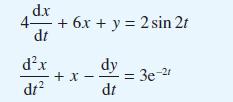
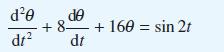
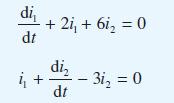
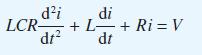
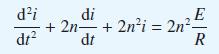
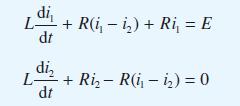
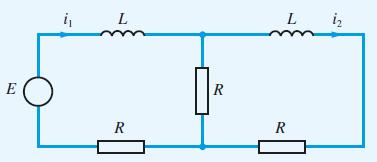
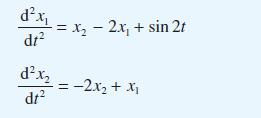
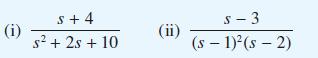
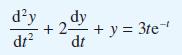
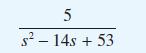
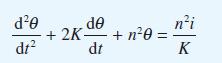
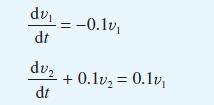
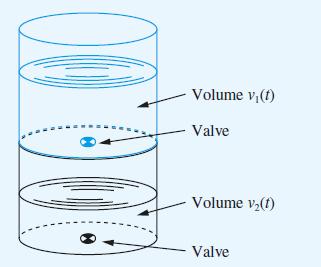
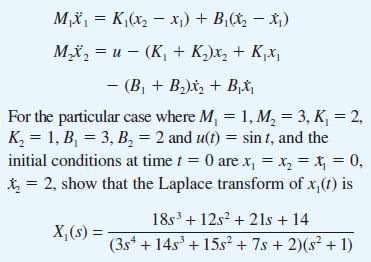
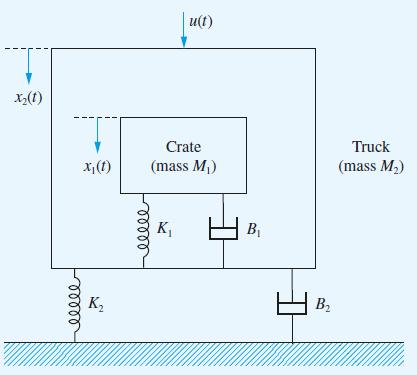
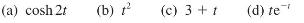
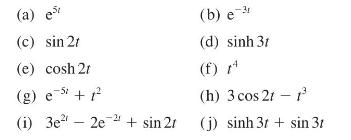
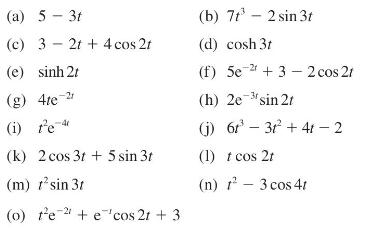

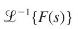
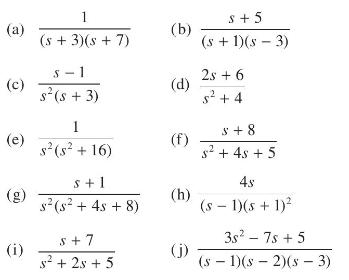
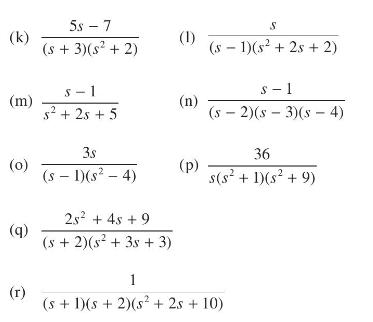
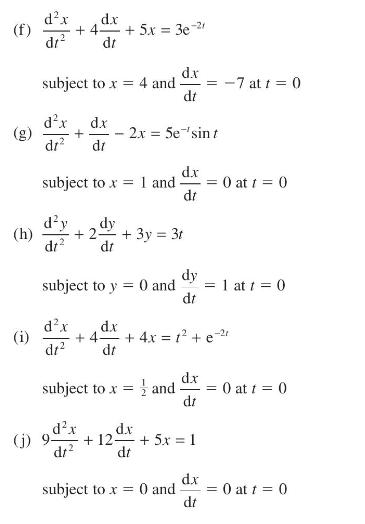
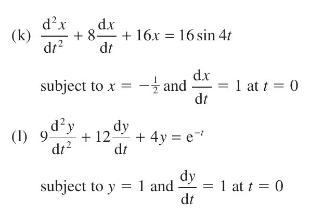
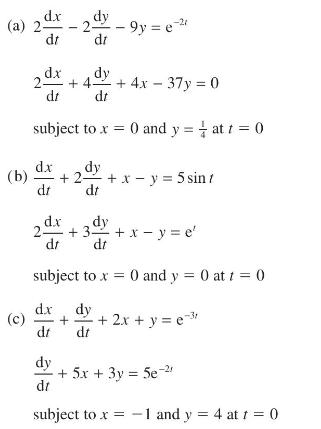
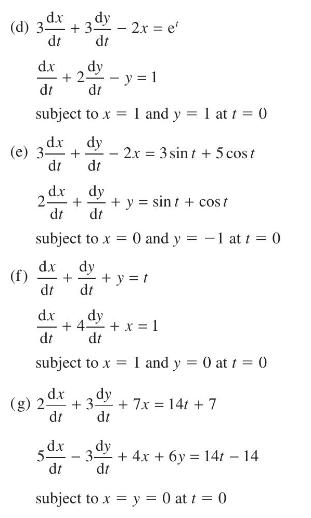
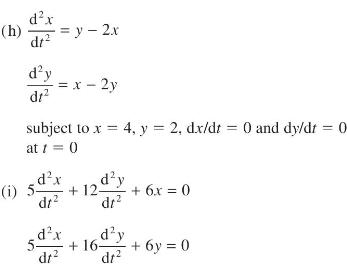
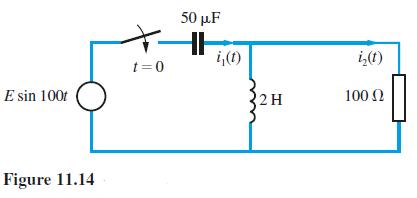
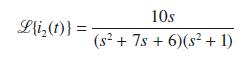
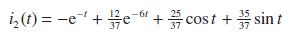
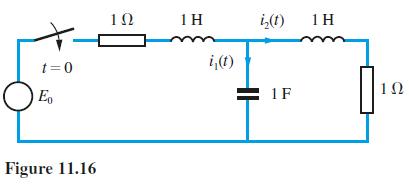
![v(t) = 10 sint Figure 11.15 t=0 202 i, (t) 1H 2 H M = 1 H i(t) ]](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/5/6/7/35065a8e47634e5b1705567351590.jpg)