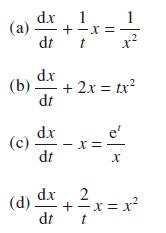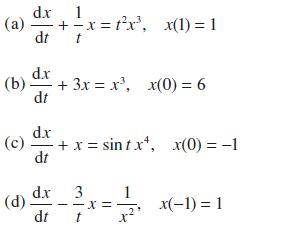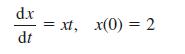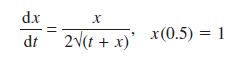![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


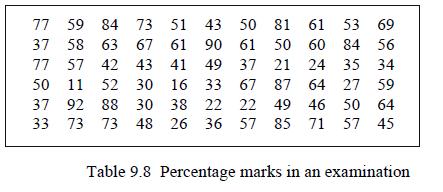
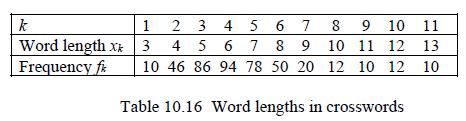
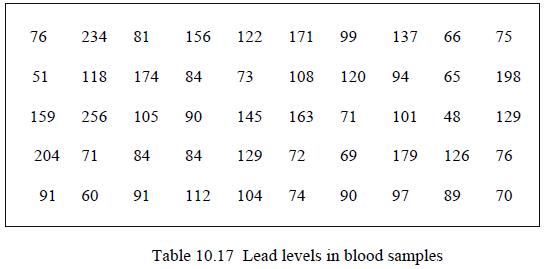
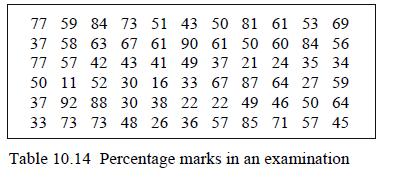
![L-1 1 [(s + 3)(s-2)]](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/4/8/6/05165a7a6e3c18181705486051396.jpg)
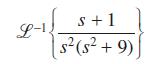
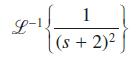
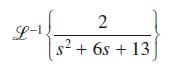
![L-1. S+7] s+2s +5](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/4/8/6/18465a7a768e082a1705486184505.jpg)
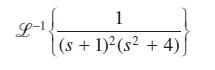
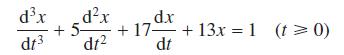

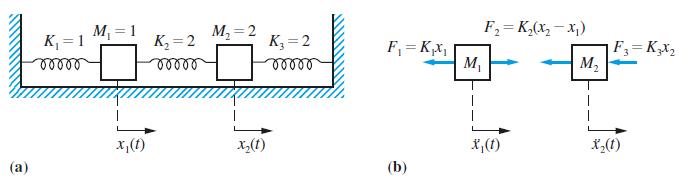
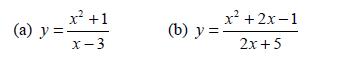

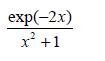
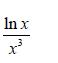
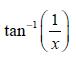
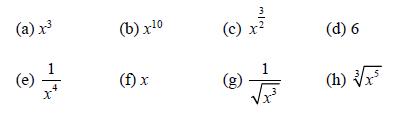
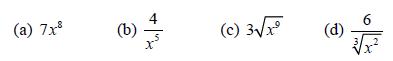
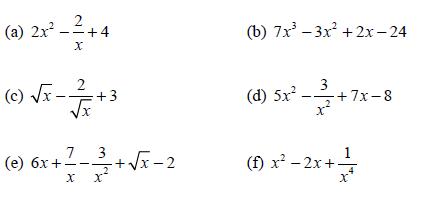
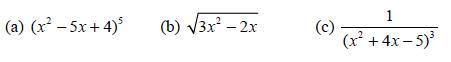
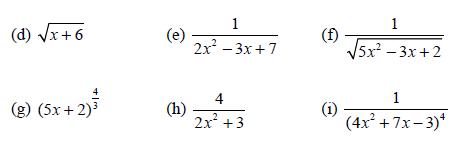
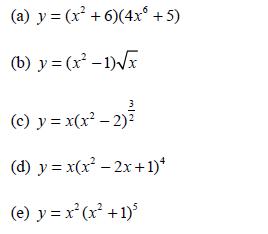
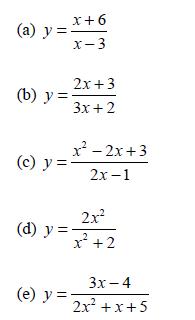
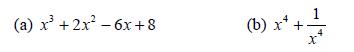

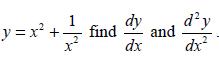
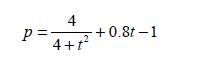

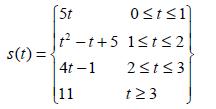
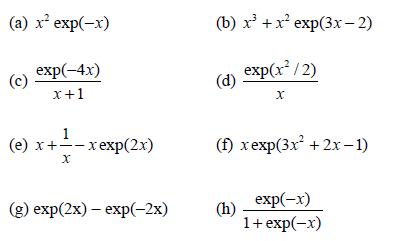
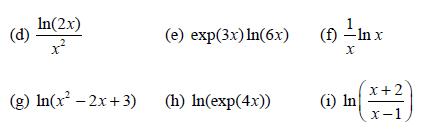
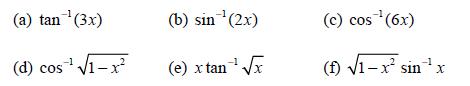
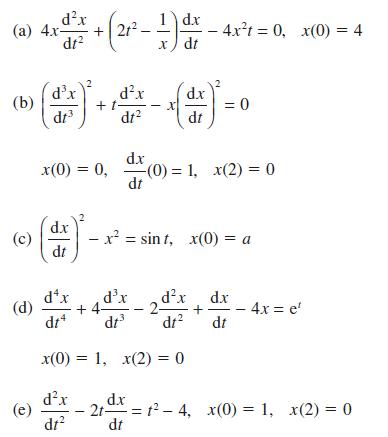
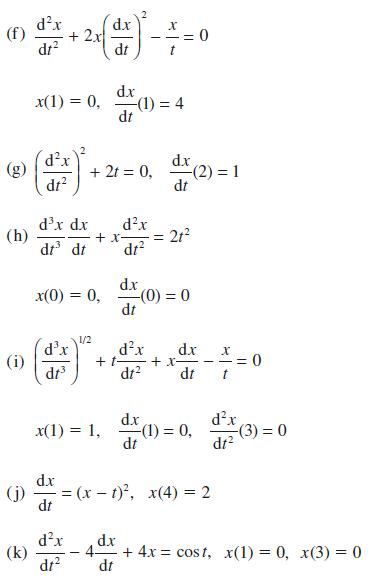
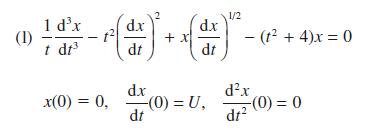
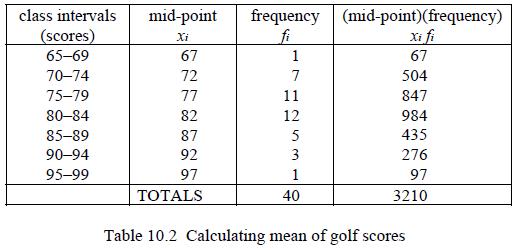
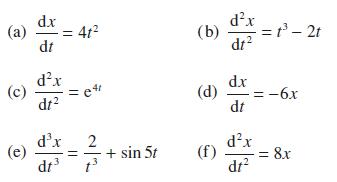
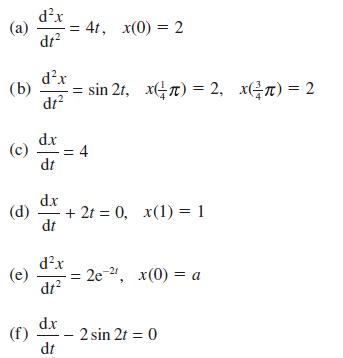
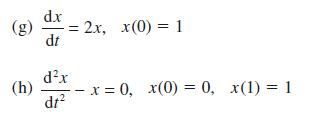
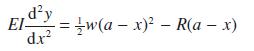
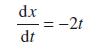
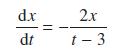
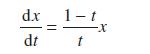
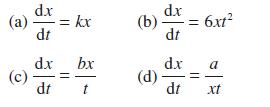
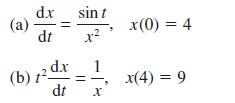
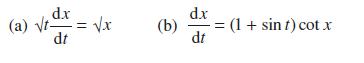
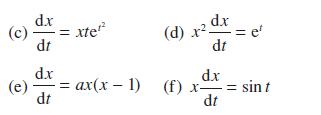
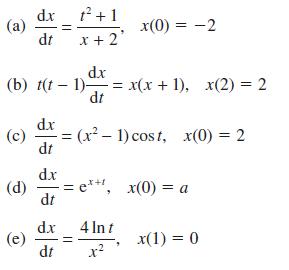
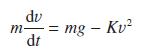
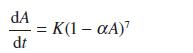
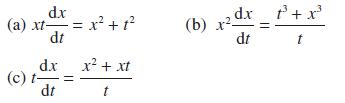
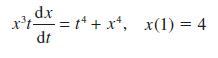
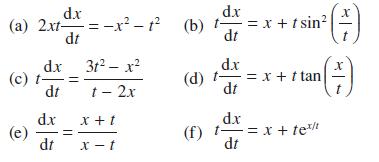
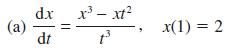
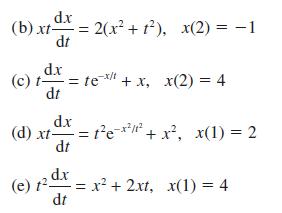
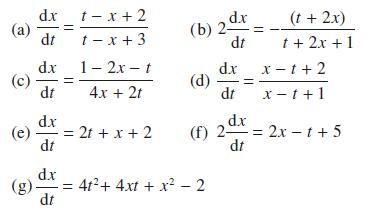
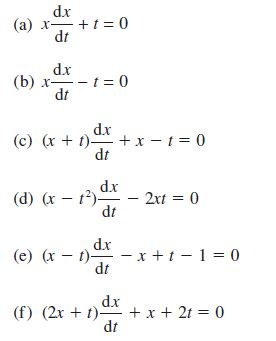
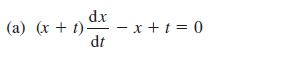
![d.x (b) txt = 0. dt d.x (c) [sin(x + 1) + x cos(x + 1)] + x cos(x + 1) = 0 dt dx (d) sin(xt). + cos.xt = 0 dt](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/3/9/2/07965a637cfdebe61705392081687.jpg)
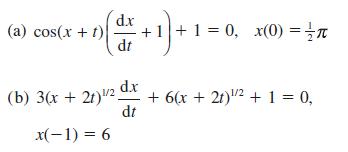
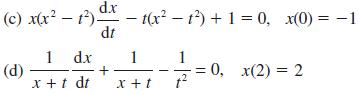
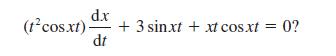
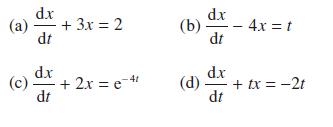
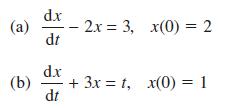
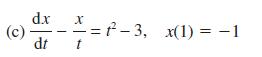
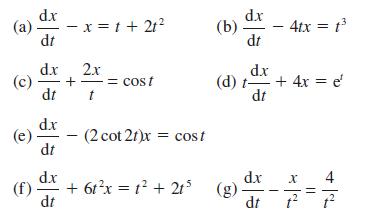

![pd dQ A dt + + ( + + B + r)]Q = Q = pgh (10.7)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/3/9/4/24765a640479186a1705394249463.jpg)