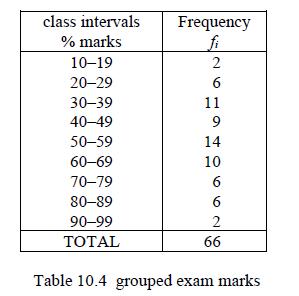
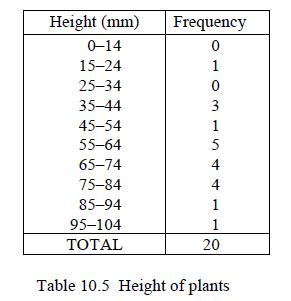
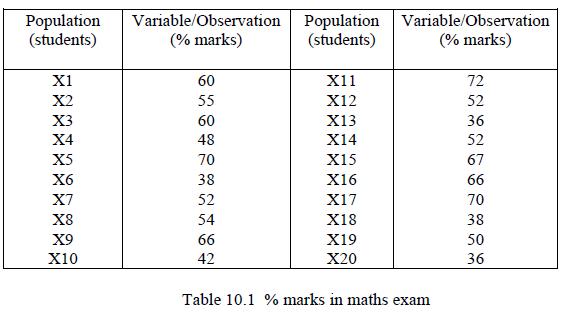
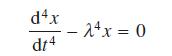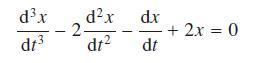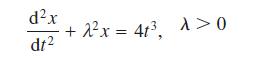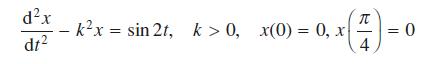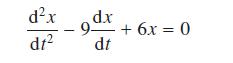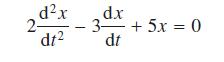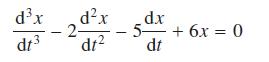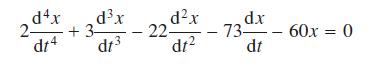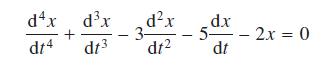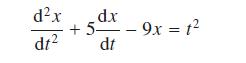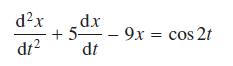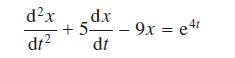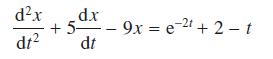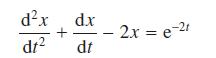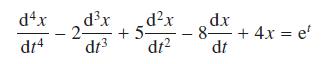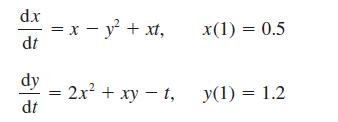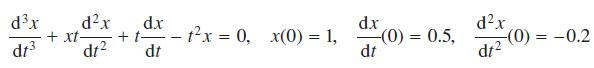![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


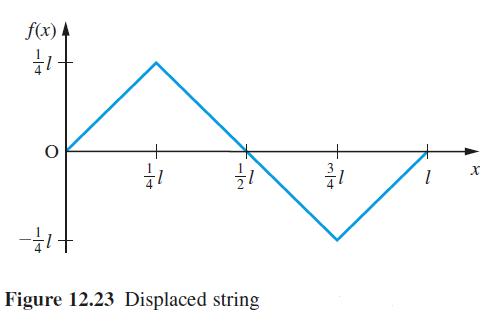
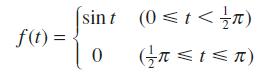
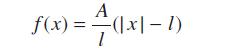
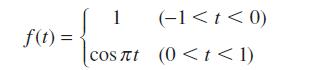
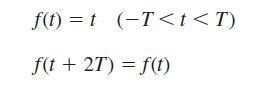
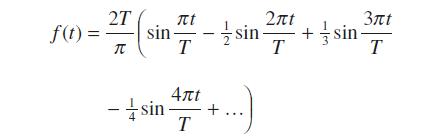
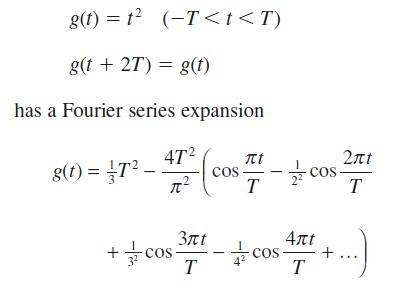
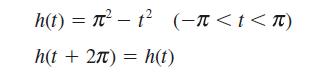
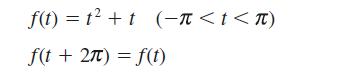
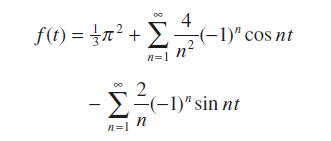
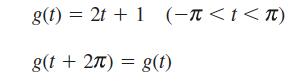
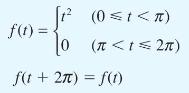
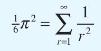
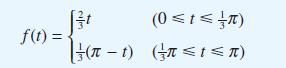
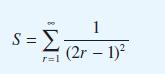
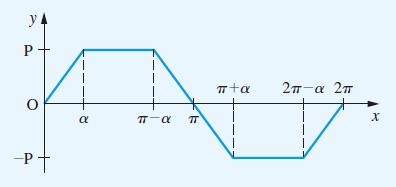
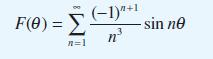
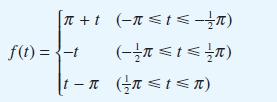
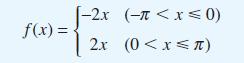
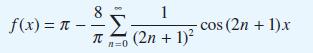
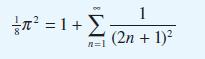
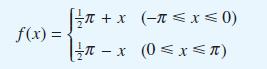
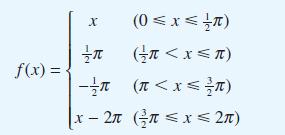
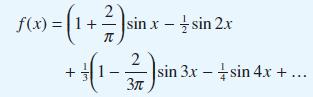
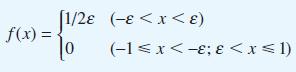
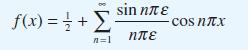
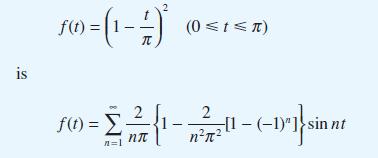
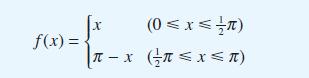
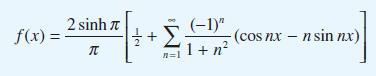
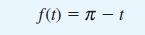
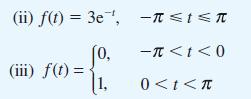
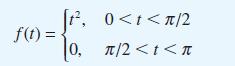
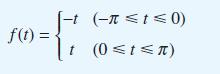
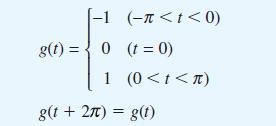
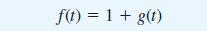
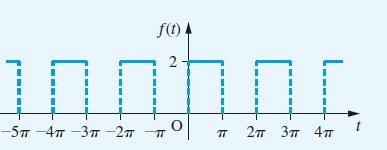
![dx 1 - + x = f(t) dt has the solution 4 x = - - n=1 cos(2n-1)t + (2n-1) sin(2n-1)t (2n-1)[1+ (2n-1)]](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/5/8/3/25565a92297116e81705583254869.jpg)
![1 202 (1-cost) y = 4 10 cos(2n +1)t - cos cot (2n +1)[w (2n + 1)]](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/5/8/3/35965a922ff616de1705583359191.jpg)
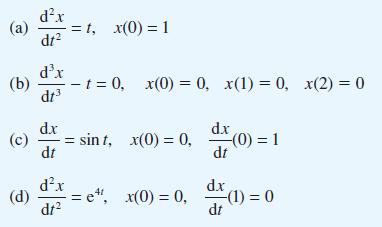
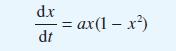
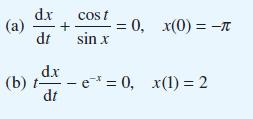
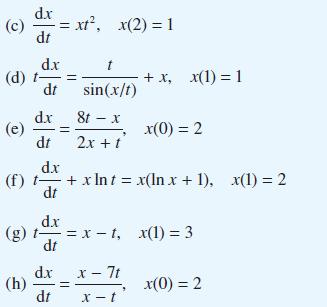
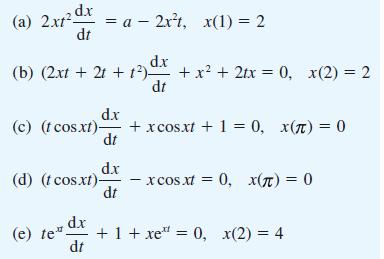
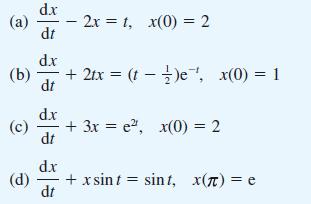
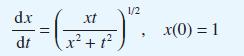
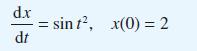
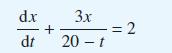
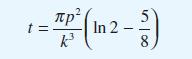
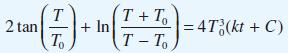
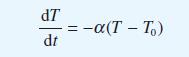
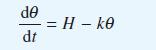
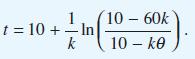
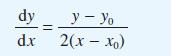
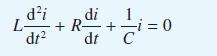
![(a) L[x(1)] = f(t) dx +(sin t) - 9x + cost = 0 dt dx dt](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/4/6/8/56265a762923a02d1705468565086.jpg)
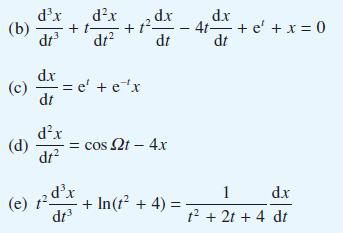
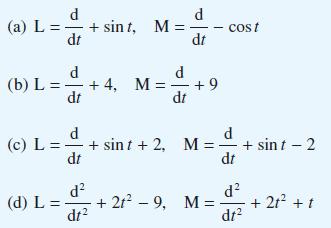
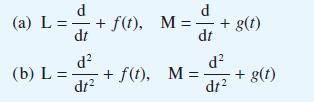
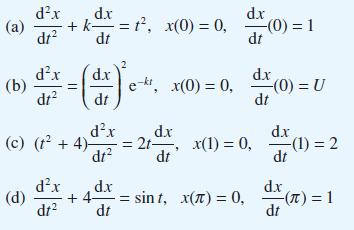
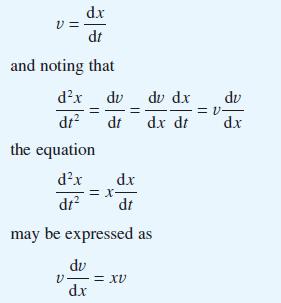
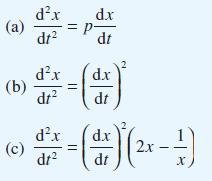
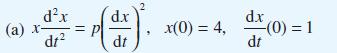
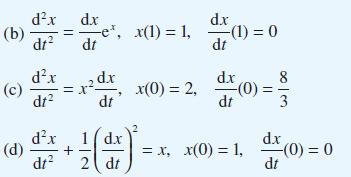

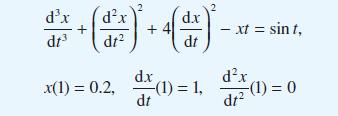
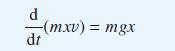
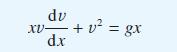
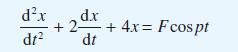
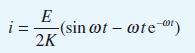
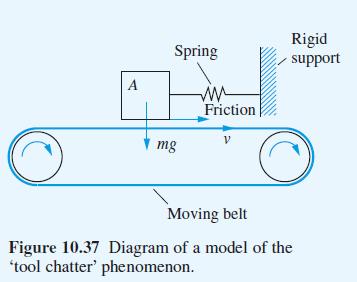
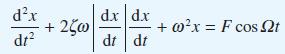
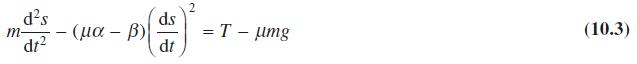

![pd dQ A dt + ( a + B + r)] = Q = pgh (10.7)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/4/7/4/50365a779c76b7291705474503213.jpg)
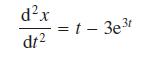
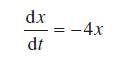
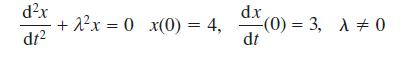
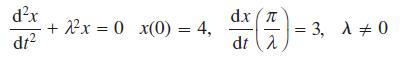
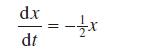
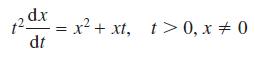
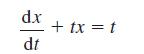
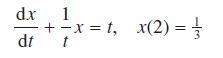
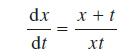
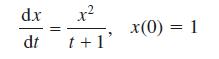
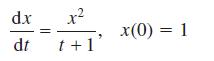
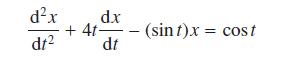
![L[ax + bx] = aL[x] + bL[x] for all functions x, and x and all constants a and b. (10.36)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/4/7/5/85865a77f122281d1705475857033.jpg)