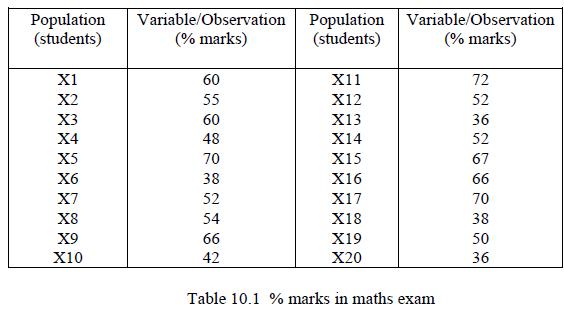
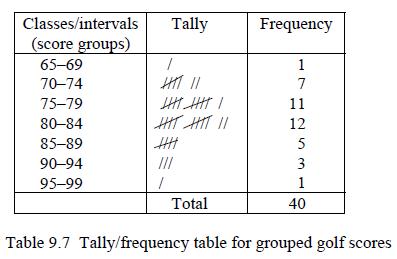
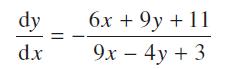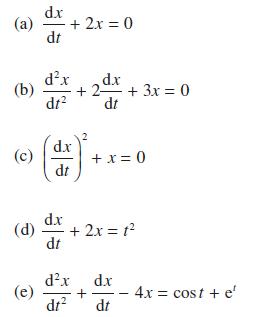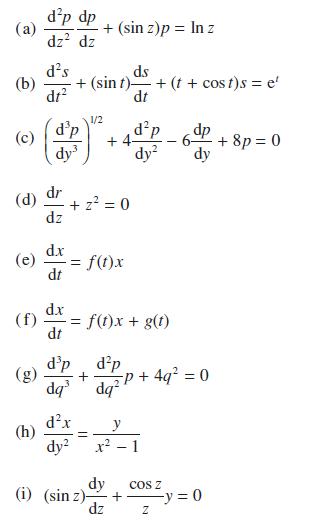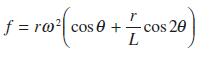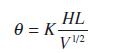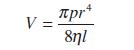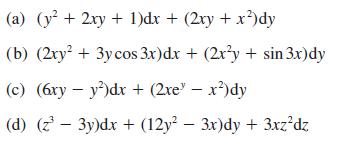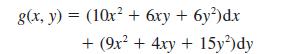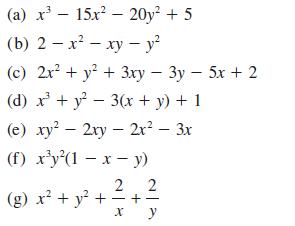![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


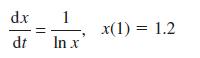
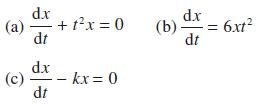
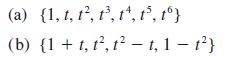
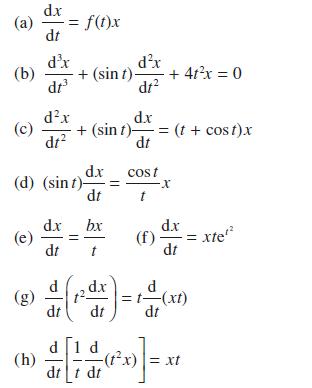
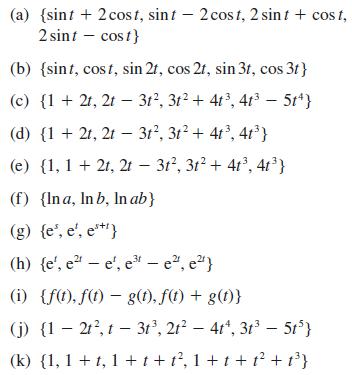
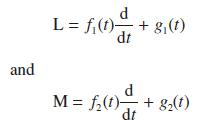
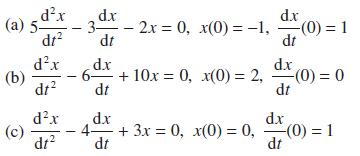
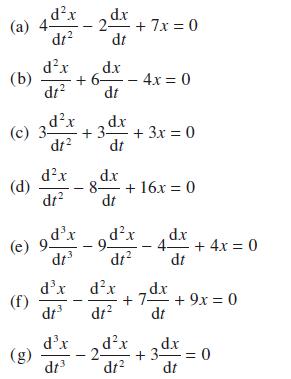
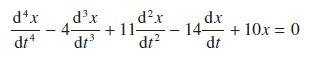
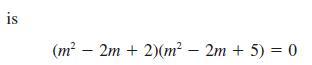
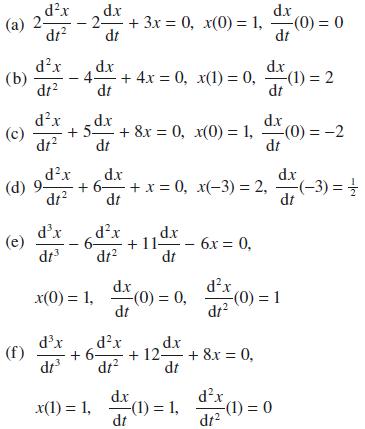
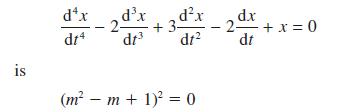
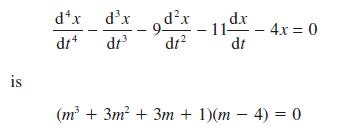
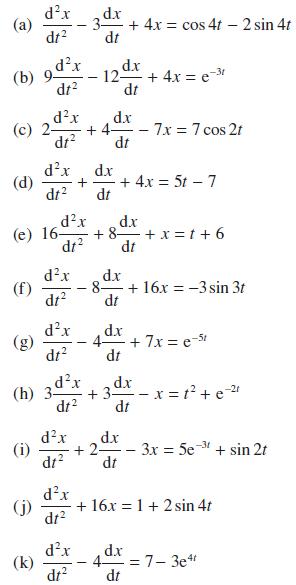
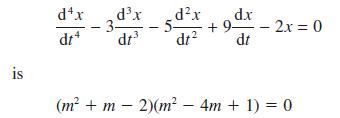
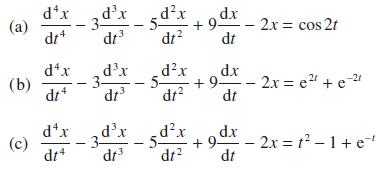
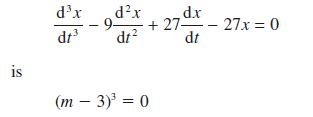
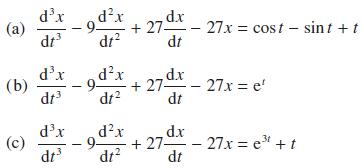
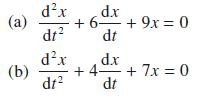
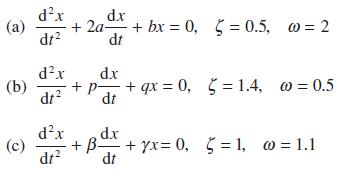
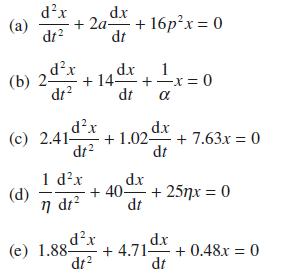
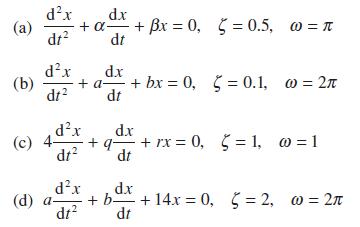

![Show that dA (0)/d2] is minimized when = . The two values of that minimize the maxima of |dA/d2 and dA(0)/d2](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/3/9/6/75865a64a1686e881705396760381.jpg)
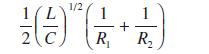
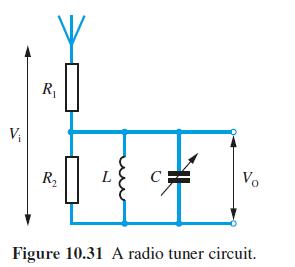
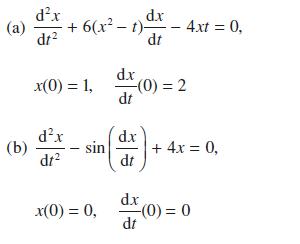
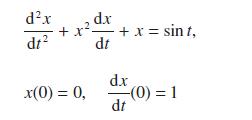
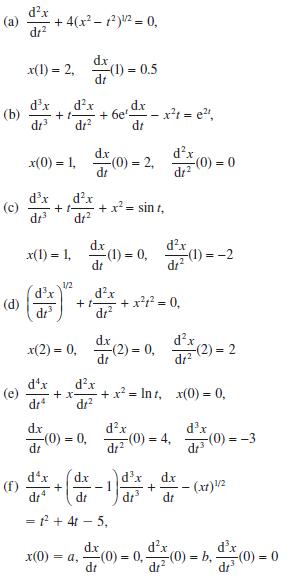
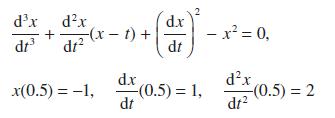
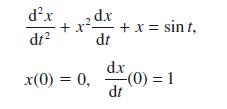
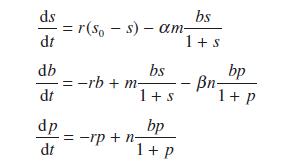
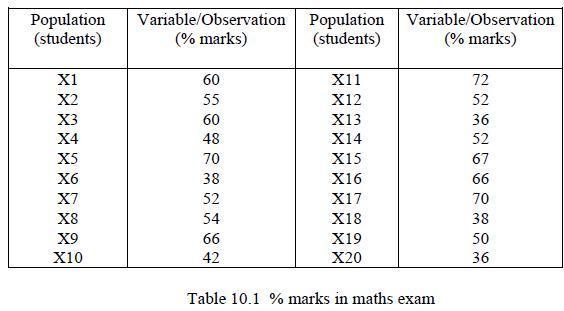
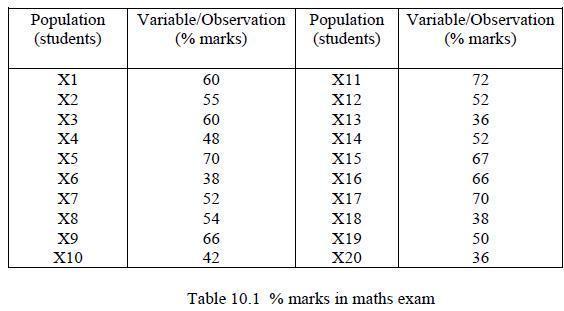
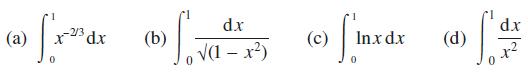
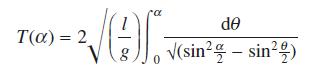
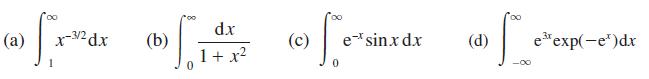
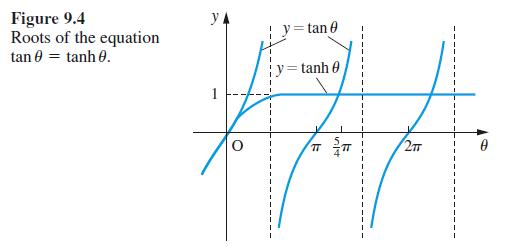
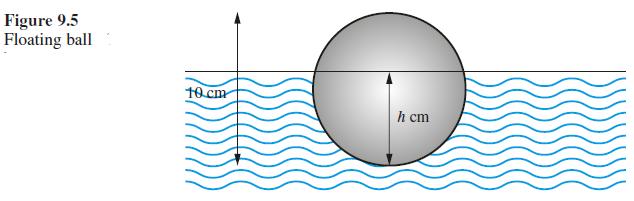
![L = 2[1 (Rr)]/ + (R + r) + 2(R - r) sin - R-r](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/3/8/1/00665a60c8ee41971705381008969.jpg)