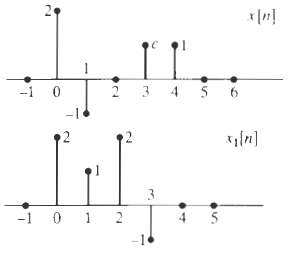
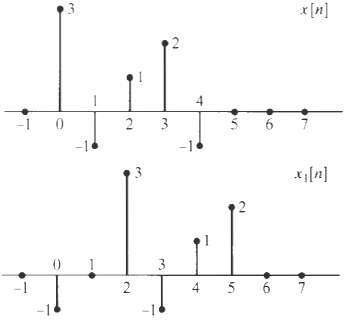
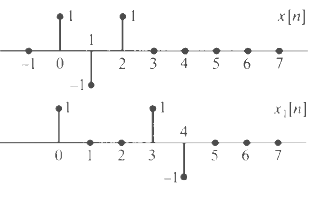
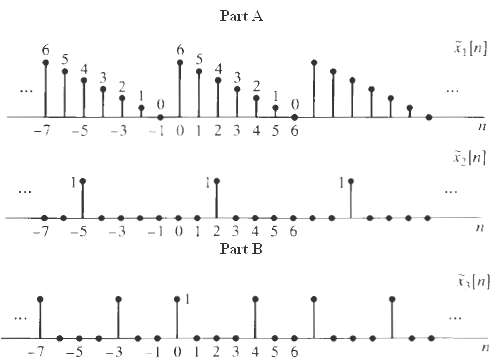
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


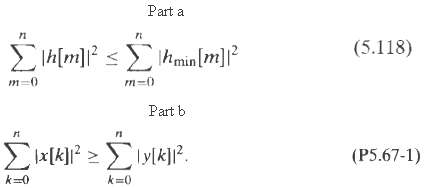
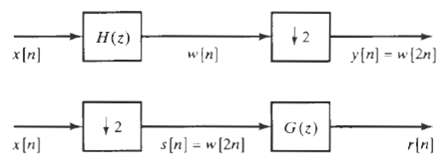
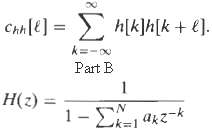
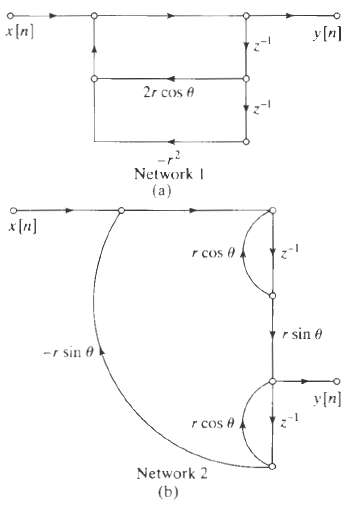
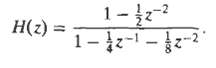
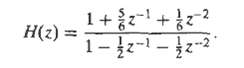
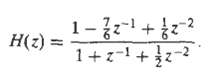
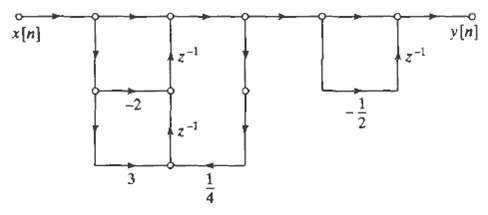
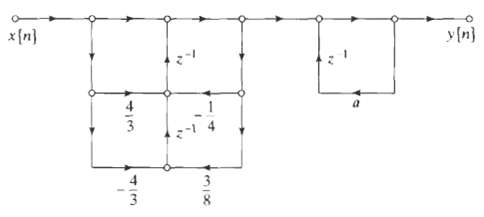
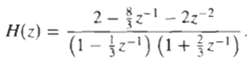
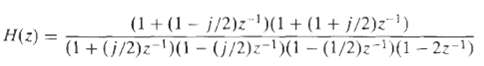
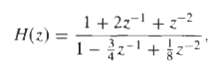
![0 <n< 14, otherwise. hlnl = { i3 (1 + cos[(2r/15)(n – no)]), 0, Part B je-i2an0/15 1 – ei2n/157-1 jei2ano/15 1 – e](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1550/1/4/0/3065c654392783301550140305328.jpg)
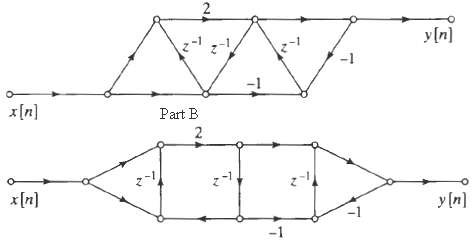
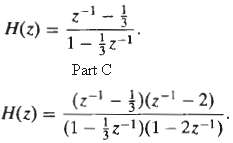
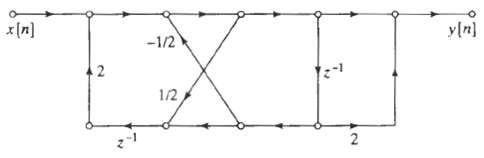
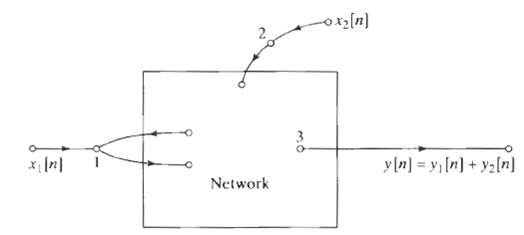
![bo y(n) y[n] x[n} x[n] bị b1 (a) (b) x[n] y[n} b1 (c)](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1550/1/4/1/3755c6547bf9f64f1550141375029.jpg)
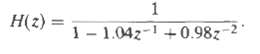
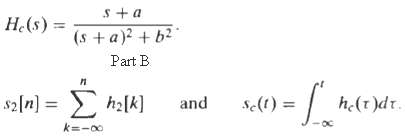
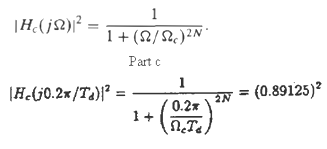
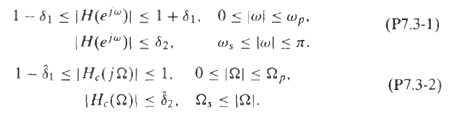
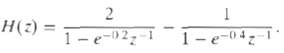

![0 < [w] < 0.27, 0.37 < |w| < 0.4757. 0.5257 < lwl < . 0.9 < H(ej](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1550/1/4/2/4515c654bf3859181550142450357.jpg)
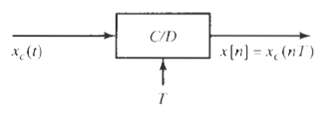
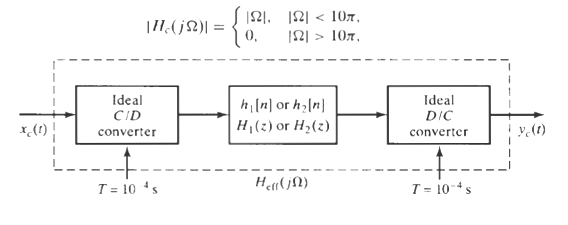
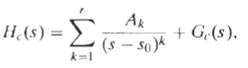
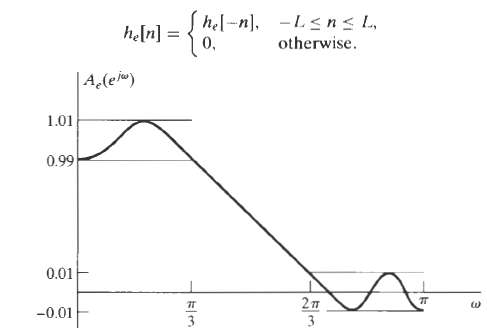
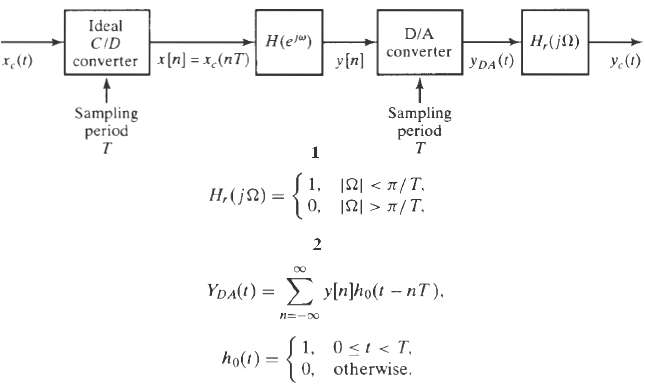
![Pait A d* y(t) ak drk d'x(t) Σα -Σ dt' k=0 1=0 ara k)ty[r]} = b,A](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1550/1/4/5/3145c6557220b4231550145313345.jpg)
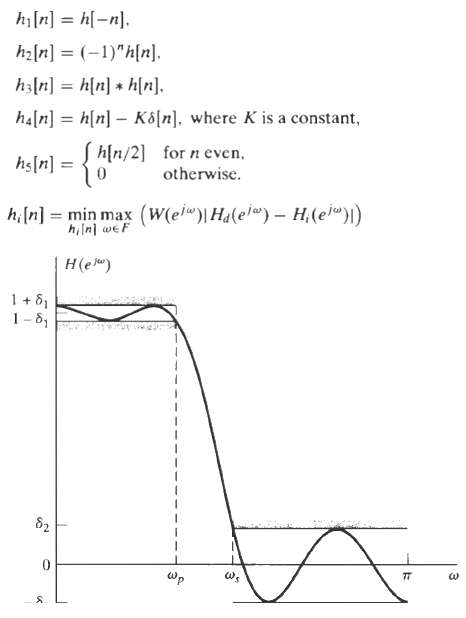
![arei(2zk!/10 *) X, (1) = k=-9 n10-3 x[n] = x, 6.](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1550/1/4/5/9635c6559ab06be91550145962343.jpg)
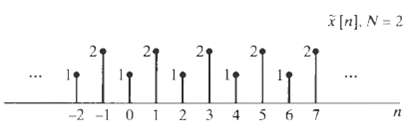
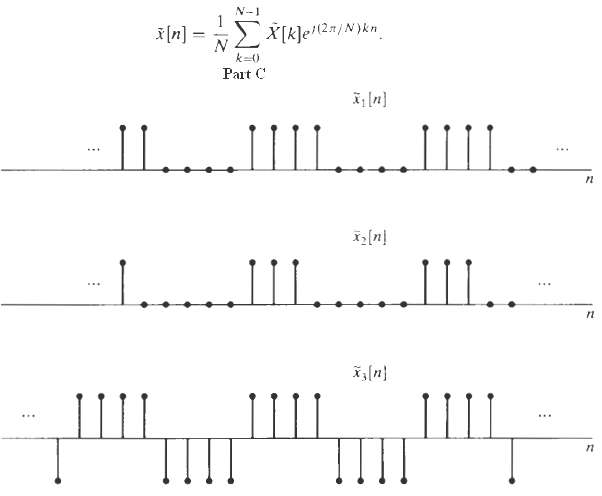
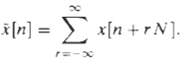
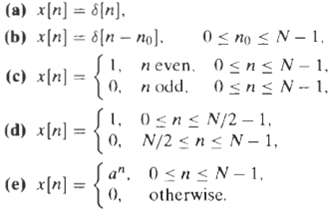

![Ь 0 1 2 3 4 5 6 7 8 x2{n] 0 1 2 3 4 5 6 7 8 п](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1550/1/4/6/9165c655d64e0bf11550146916225.jpg)