![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()



![|e[n]|2 Awr[n] = -µÎJ[k]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1549/2/7/8/2175c581c098a73f1549325015555.jpg)
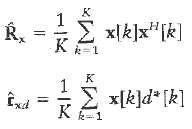
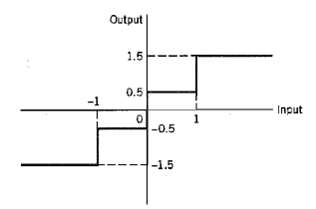
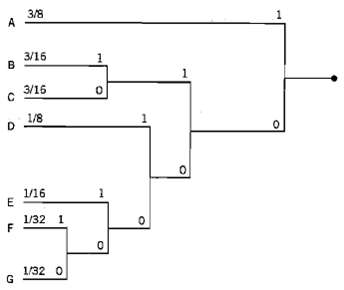
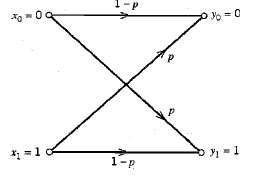

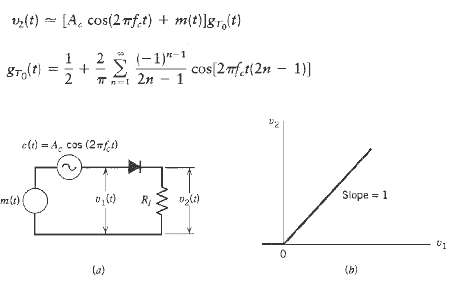
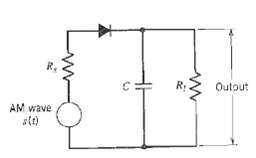
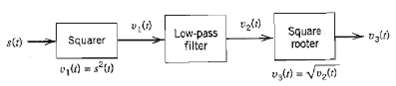
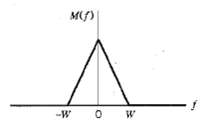
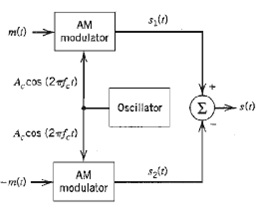
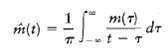
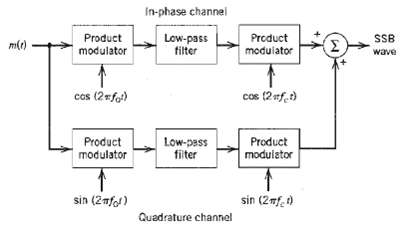
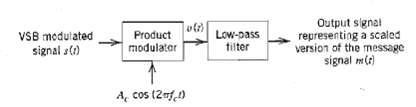
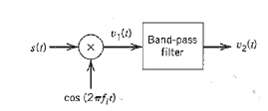
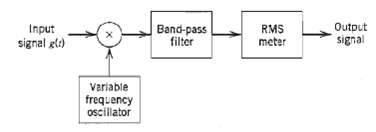
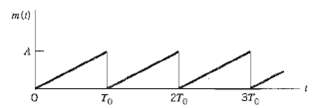
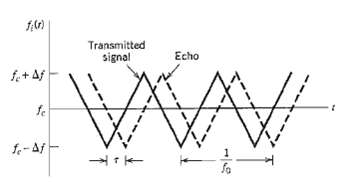
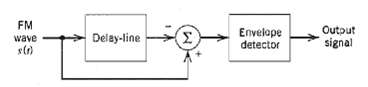

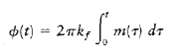
![z(t) = sgn[s(t)] s(t) style=](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1549/0/9/0/9075c55405b237491549090907733.jpg)