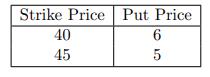
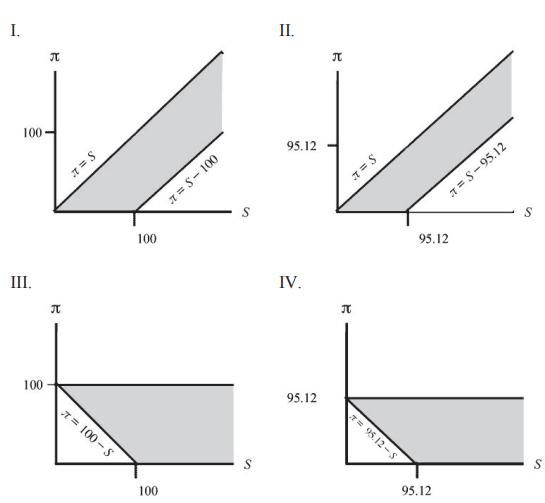
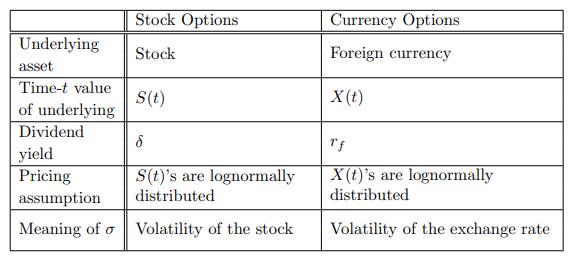
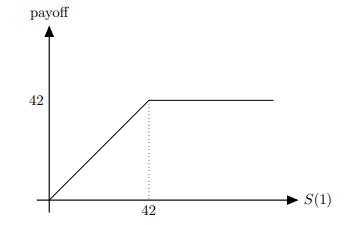
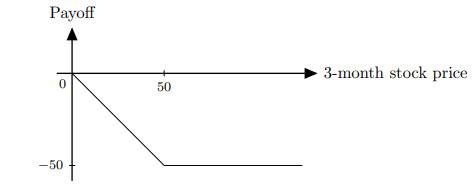
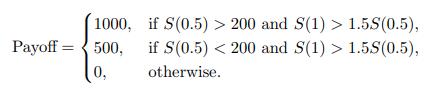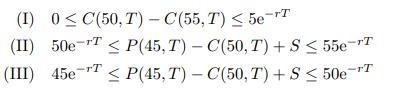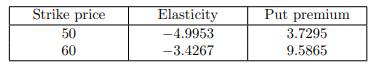![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


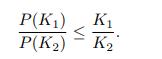
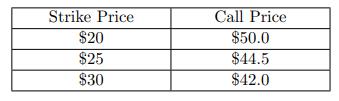
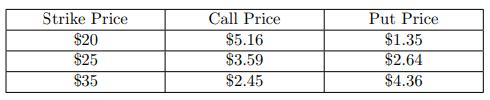
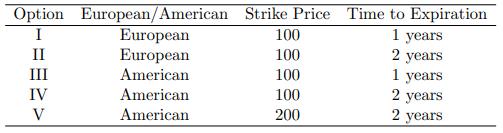
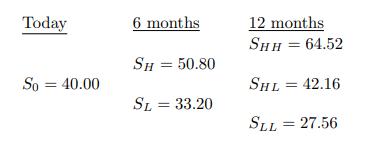
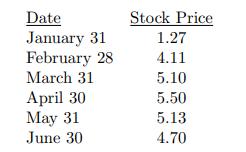
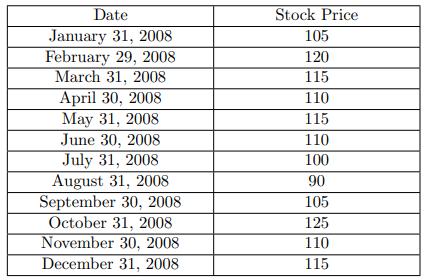

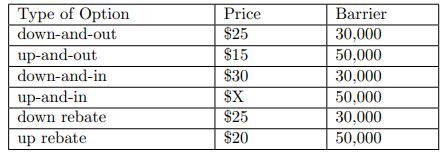
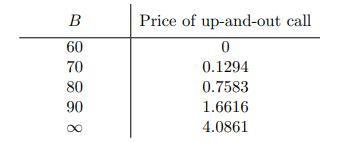
![B Not Hit 0 B Hit B Not Hit 2 x max[S(0.5) - 60,0] B2 Hit max[S(0.5) - 60,0]](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/6/5/4/380655ded2c5c18e1700654379873.jpg)