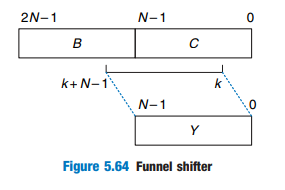
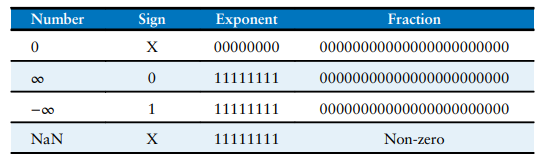
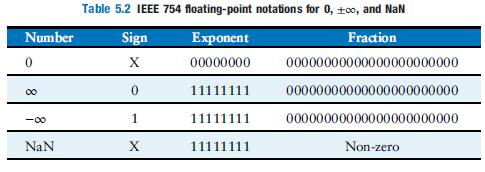
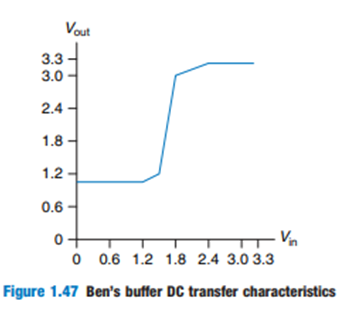
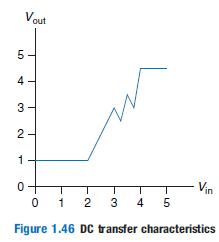
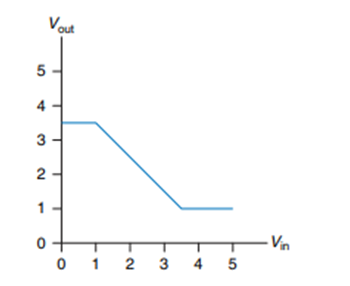
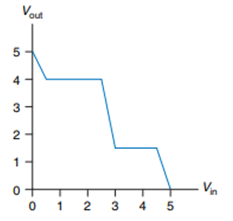
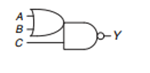
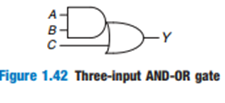
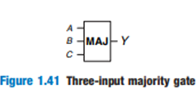
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


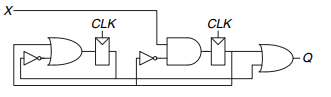
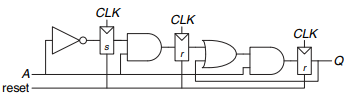
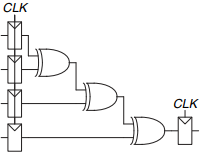
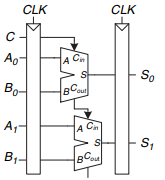

![module latch(input logic clk. input logic [3:0] d. output reg [3:0] q): always @(clk) if (clk) q <= d: endmodule](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1547/3/0/9/6815c3a1271130d81547292320907.jpg)
![module gates (input logic [3:0] a, b. output logic [3:0] y1. y2. y3. y4. y5): always @(a) begin yl = a & b; y2 = a | b:](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1547/3/0/9/7015c3a12854c3a51547292341166.jpg)
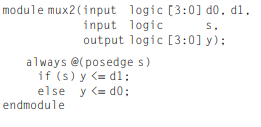



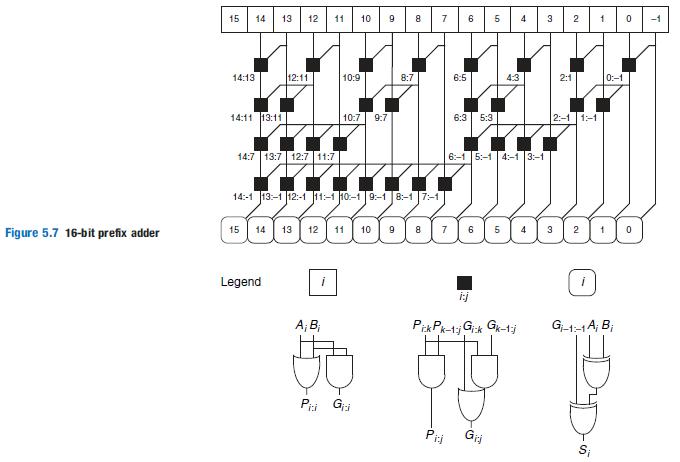
![A N. F2 *N BB Cout [N-1] S YN F1.0 to Zero extend](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1547/4/6/2/1455c3c66015372a1547444780604.jpg)