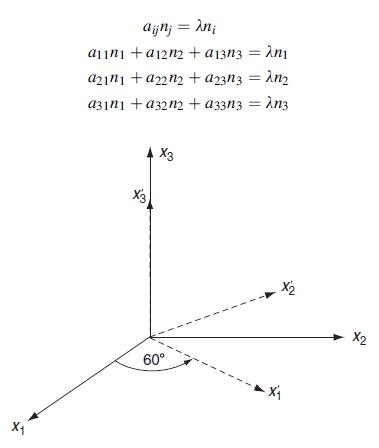
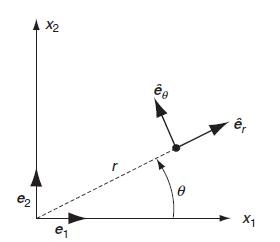
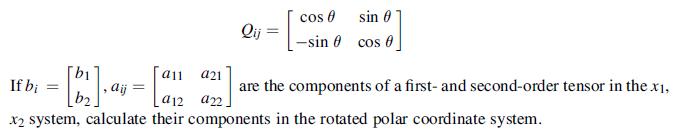![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


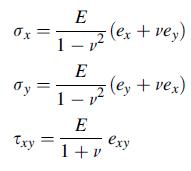
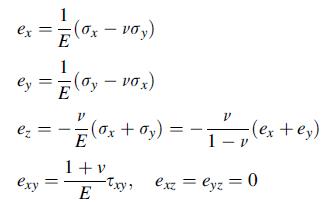
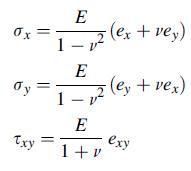
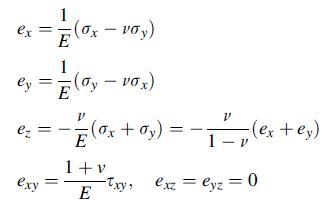
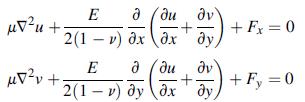
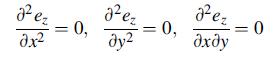
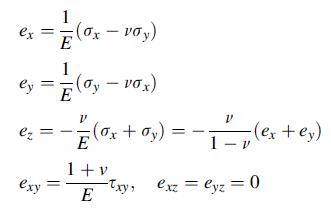


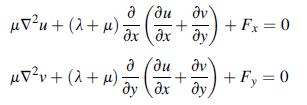
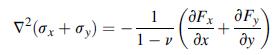

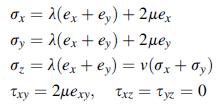
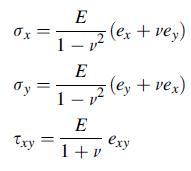
![0x = u = M Mxy EI dy = Txy = 0 M 2EI V= [vy + x-]](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1704/9/6/5/579659fb5cb6af7c1704965578187.jpg)

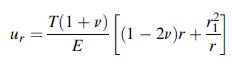
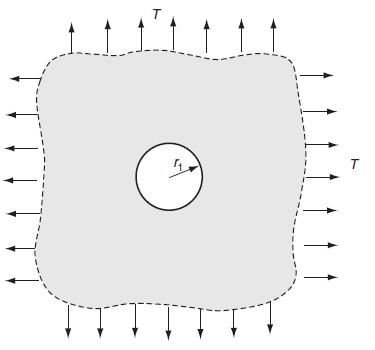

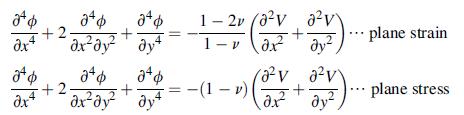
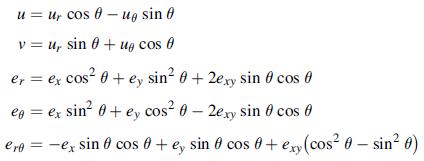
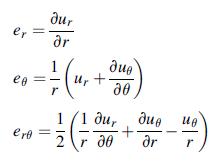
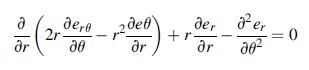
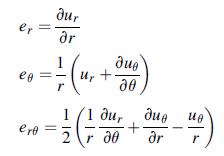

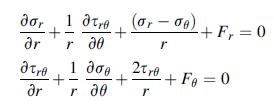
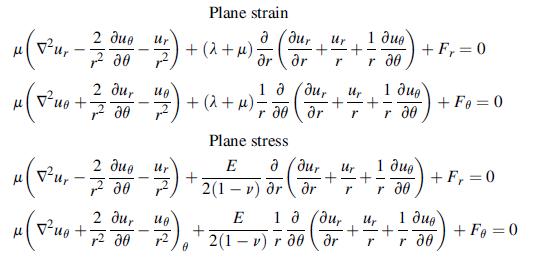
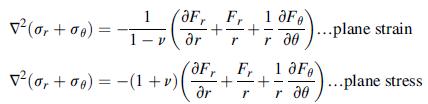
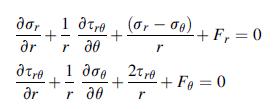

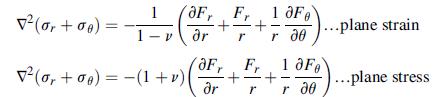
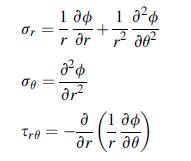
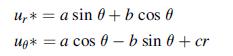
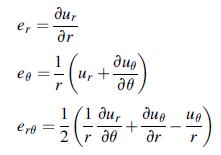
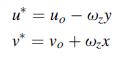
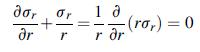
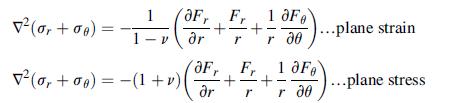
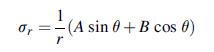
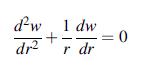
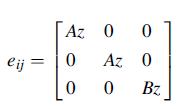
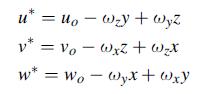
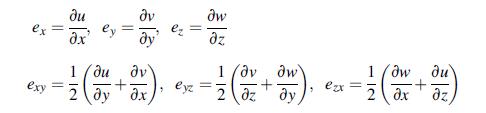
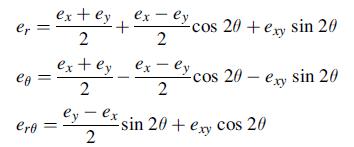
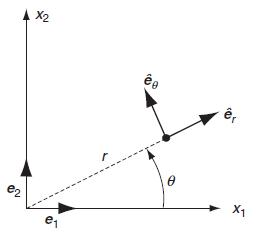
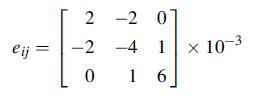
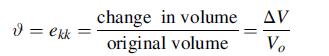
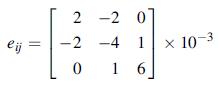
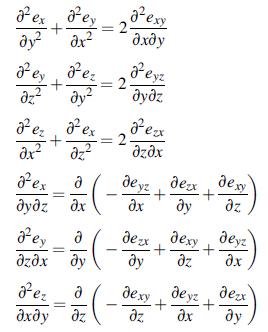
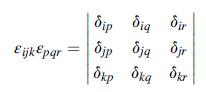
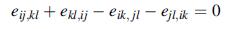
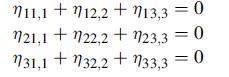
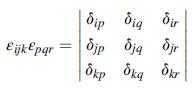
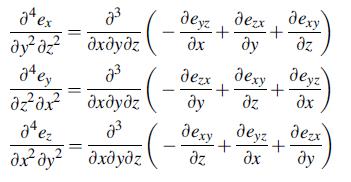
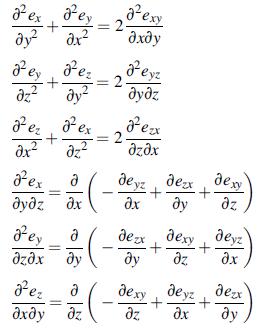
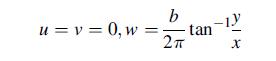
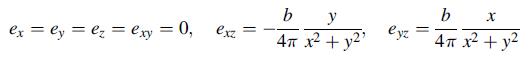
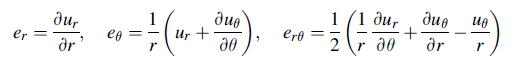
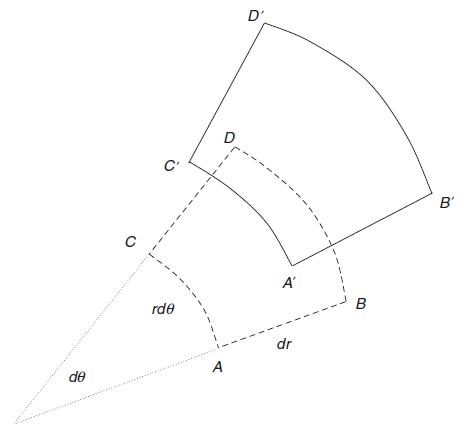
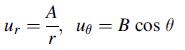
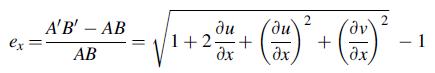
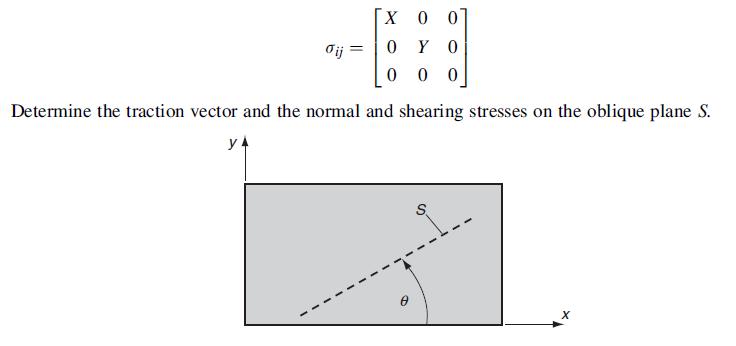
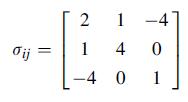
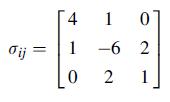
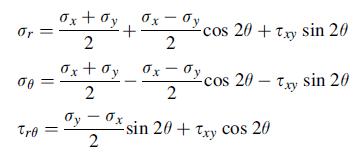
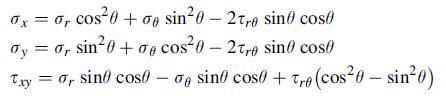
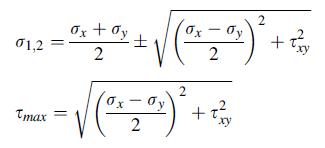
![Joct = 3 (0x + a + a) ay Toct= - [(ox ay) + (ay a) + (a 0x) + 62y +673 +67 ] / 1/2 - -](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1704/8/6/9/373659e3dfd301a41704869372800.jpg)
![1 N = 0oct=3(01+02 +03) = 30 kk = 3/1 S = Toct 1 = 3 [(0-0) + (02-03) + (03-0)] 1/2 - (217-6/2)/2 3](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1704/8/7/2/591659e4a8fd44bf1704872591090.jpg)
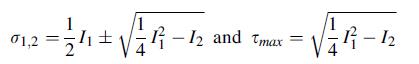
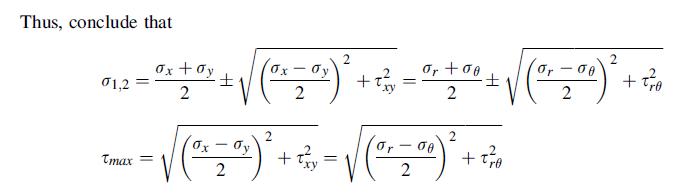
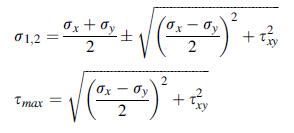

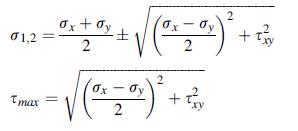
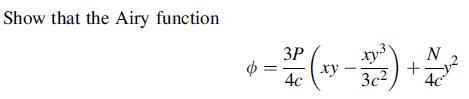

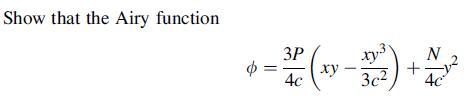
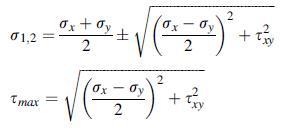

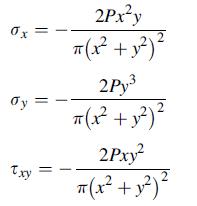
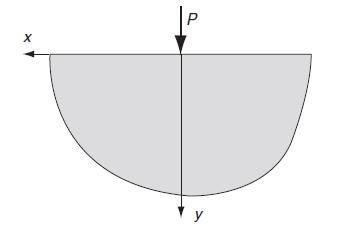
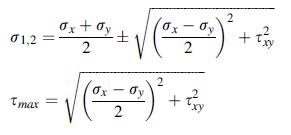
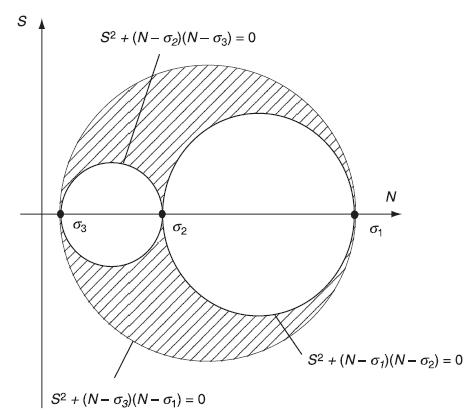
![S = [nn(01 02) + nn3(02 03) + nn(03 01)]/](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1704/8/6/9/872659e3ff069a5a1704869872019.jpg)
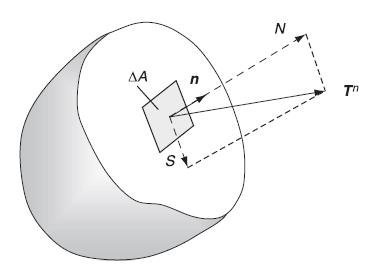
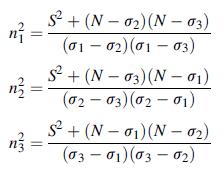
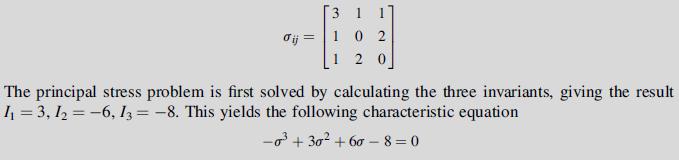
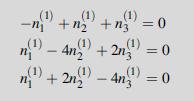
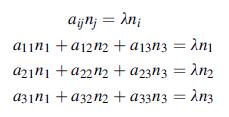
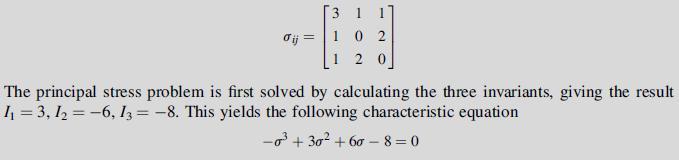
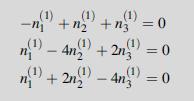
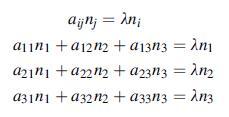
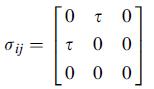
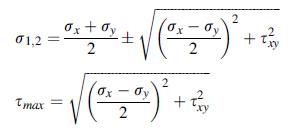
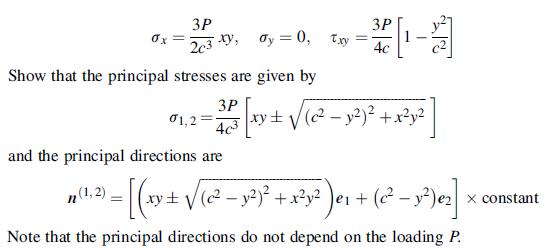
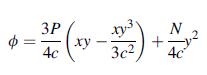
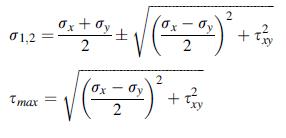
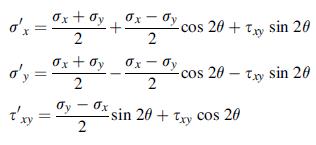
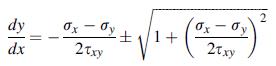
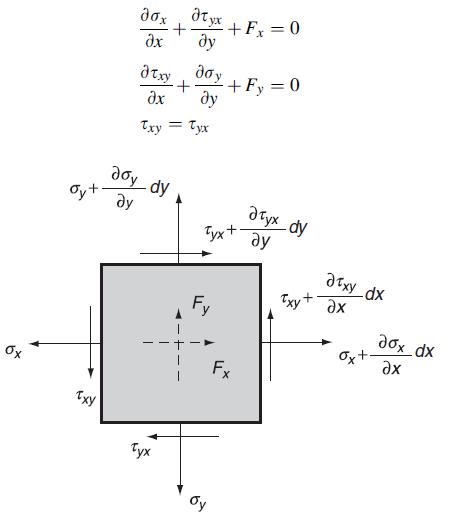
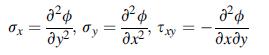
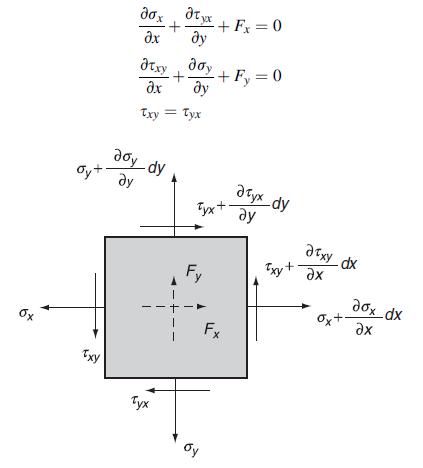
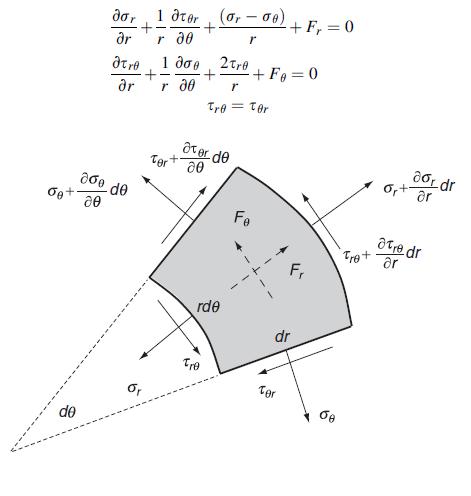
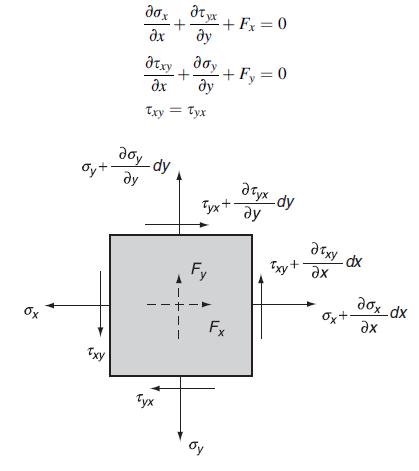
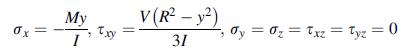
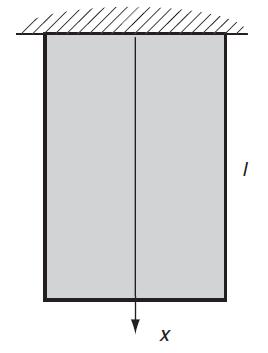
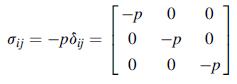
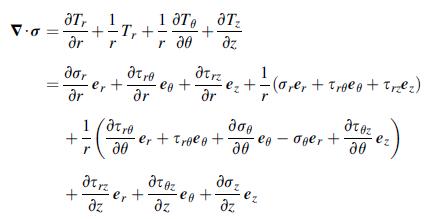
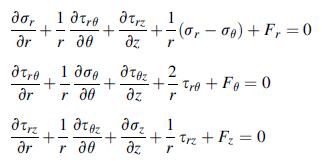

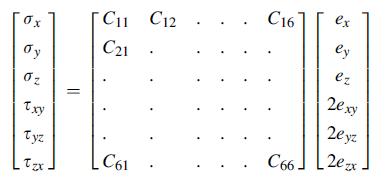
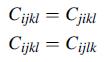
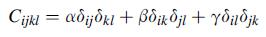
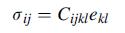
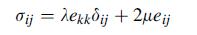
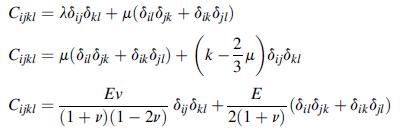
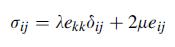
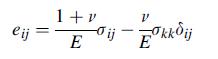
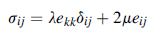
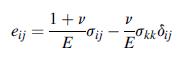
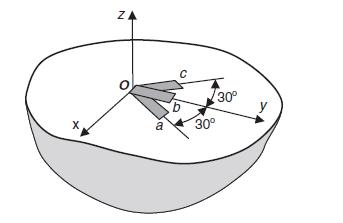
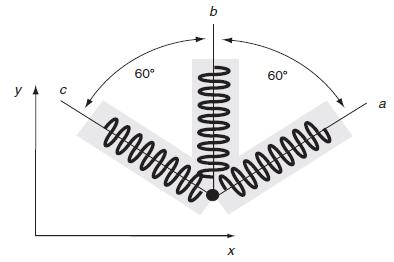
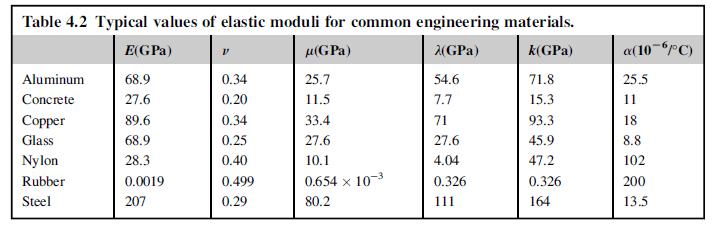
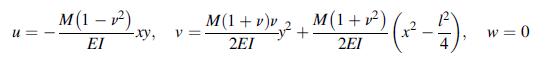
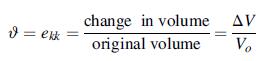
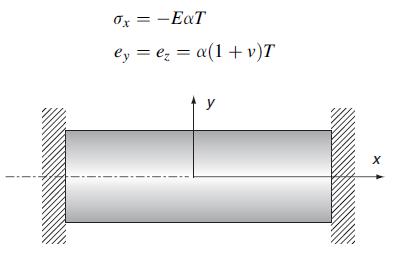
![0x dy 0 Txy = E (1 + v) (1-2v) -[(1 v)ex+v(ey + ez)] E (1 + v) (1-2v) E (1 + v)(1-2v) E exy, 1+v -[(1 v)ey](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1704/8/8/3/970659e7702192781704883969365.jpg)
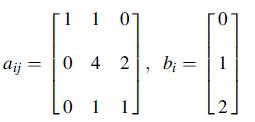
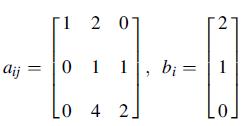
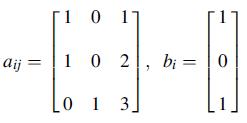
![aij z (aij + aji) +z (aij aji) = a(yj) + a[i]](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1704/8/0/1/085659d333d4b4911704801085142.jpg)
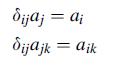
![det[ay] =lajl= = all a12 a13 a21 922 a23 a31 a32 a33 = Eijka 1a2ja3k = = Eijkailaj2 ak3](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1704/8/0/1/386659d346ac90591704801386674.jpg)