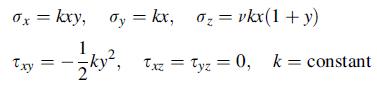![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


![2y p(s) (xs) - [ -a a [(x x) + y] 0x = = Txy = 2y ra - L ds p(s) [( x s) + x] a 2Py ds = - + [-3 - 4](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/0/5/0/57265a101cc9cf9f1705050572929.jpg)
![0x = dy = Txy a 2y p(s) (x - s) L 2- 21 a [(x s) + y] ds = p(s) -a [(x x) + 1] ra L ds == p(s) (x - s)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/0/5/0/59565a101e3534661705050595624.jpg)


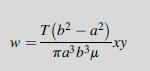
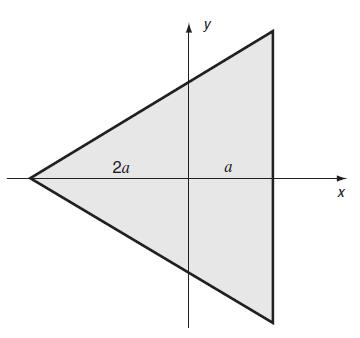
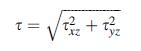

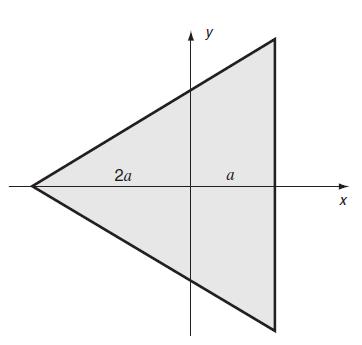
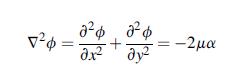
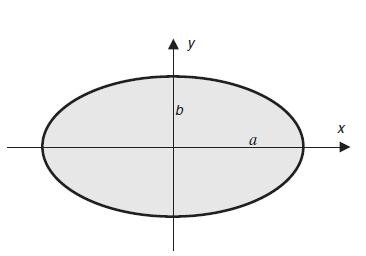
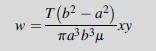
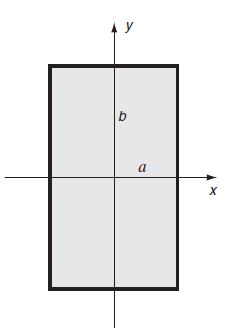
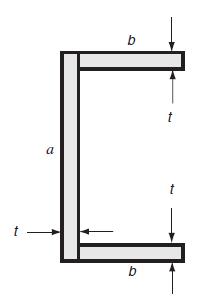
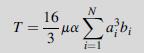
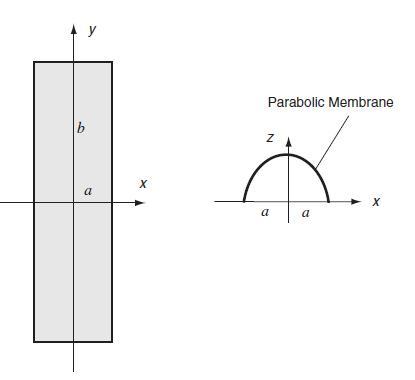
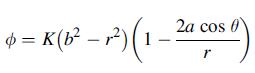
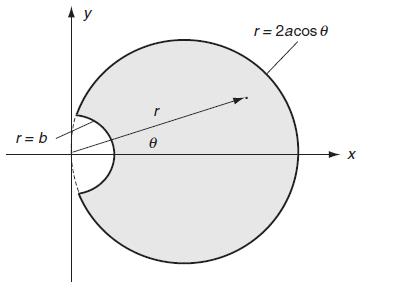
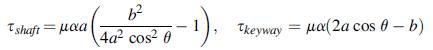
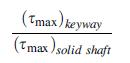
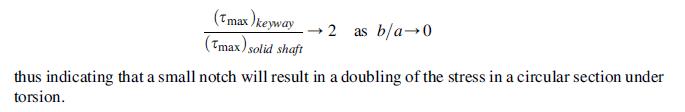

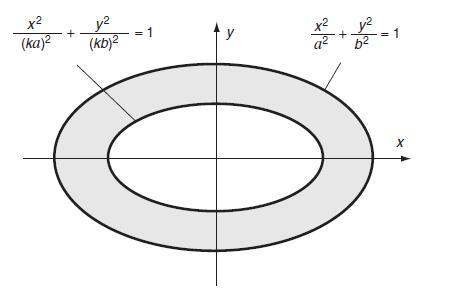

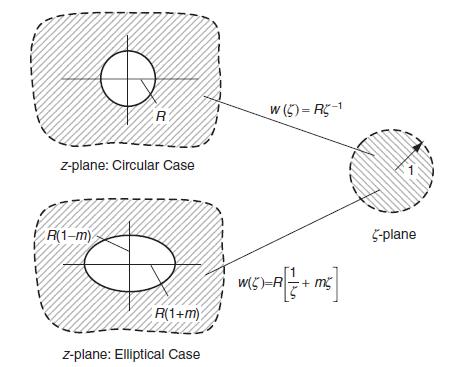
![T = rm + (1-14) ] 12]](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/0/5/6/56665a11936499f71705056566144.jpg)













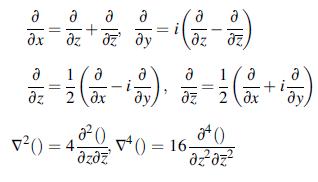
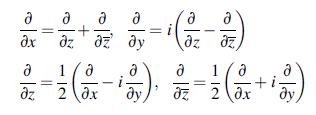
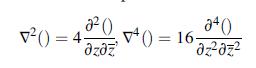
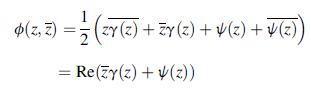
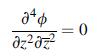
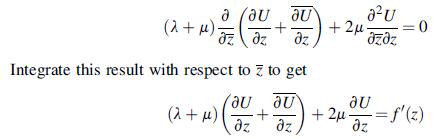
![[2(u +iv)] = [zy(2) + (3)] = (ex ey + Ziexy) where ex, ey, and exy are the strain components.](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/0/6/0/35965a12807a85ba1705060359468.jpg)
![0x + ay = 2 [Y(z) + Y (2) Oy - 0x + 2ity = 2[zy" (z)+(2)] Next solve these relations for the individual](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/0/6/0/39565a1282baafdf1705060395153.jpg)
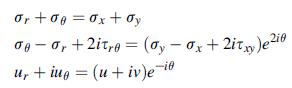
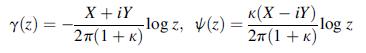

![M = * (, - )ds xd |-- I +yd B +y A ()] = Re[x(z) - z4 (z) - zZY'(z)].](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/0/6/1/14165a12b15845241705061141285.jpg)
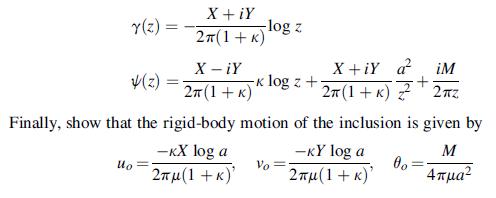





![sx Px 2=(1+}r? Px 2=(1+}r Py 21(1+}r [+] 5 -3-x, p = x2 +2](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/0/6/2/10465a12ed8a2d271705062103335.jpg)
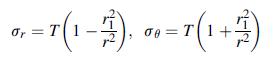
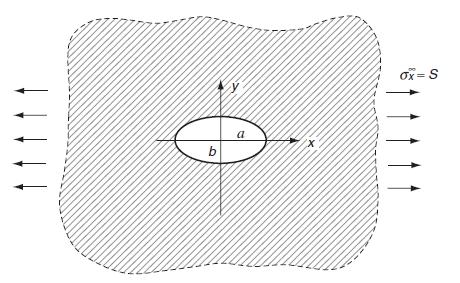
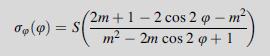
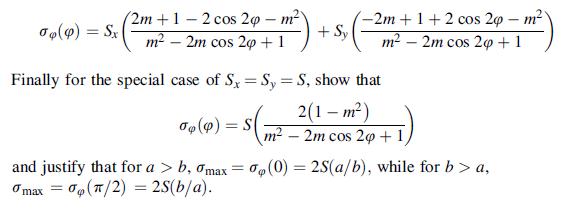
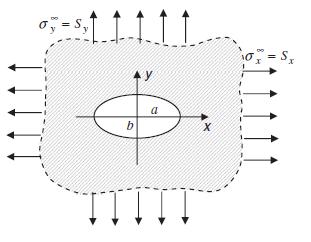

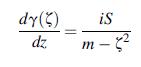
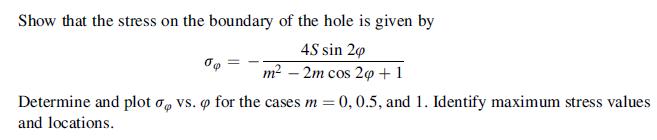
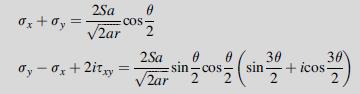
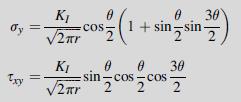
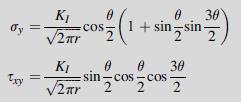
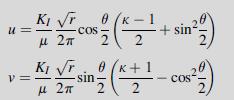
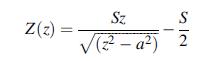
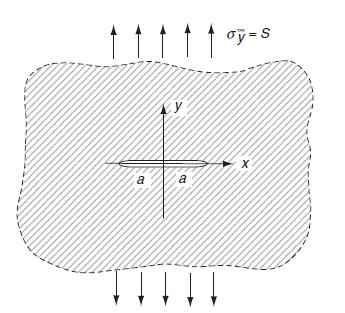

![Using the stress combination definitions (10.2.11), we eliminate the potential and find ox2 Re[y' (2)] -](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/0/6/3/91065a135e6ee4dd1705063910311.jpg)
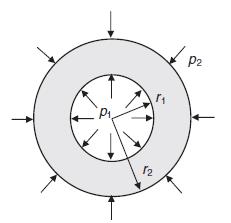
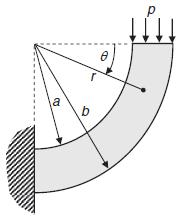
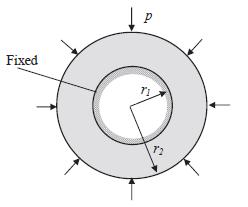
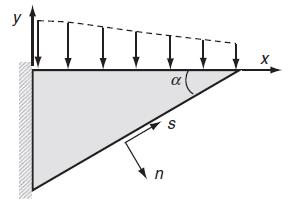
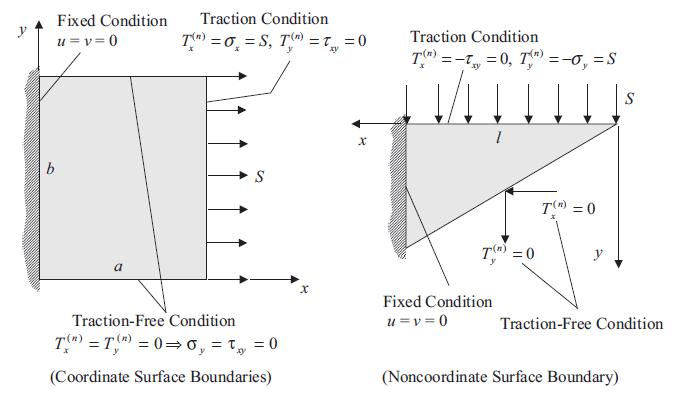
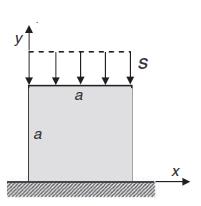
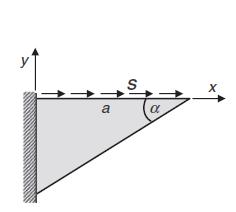
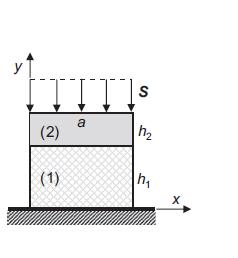
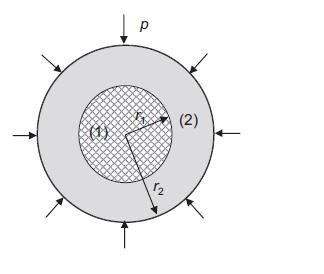
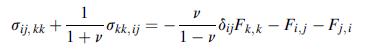
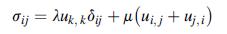
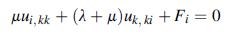
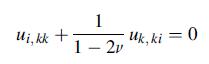
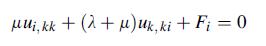
![u= W = vpgxz E V = vpgyz E pg 21 [2 +v(x + y) 1]](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1704/9/5/2/042659f80ea8d9691704952041578.jpg)
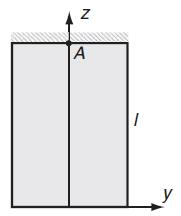

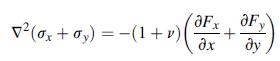
![0x = c[y +v(x - y)] oy = c[x +v(y-x)] 0 = cv(x + y) Txy = -2cvxy Tyz = Tzx = 0, c = constant #0](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1704/9/5/0/899659f7c73eaab31704950898761.jpg)
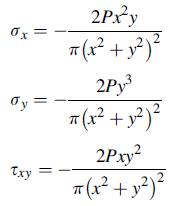
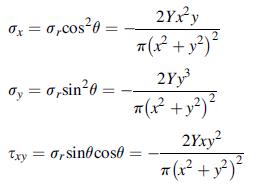
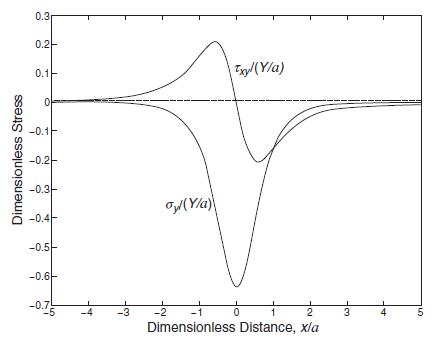
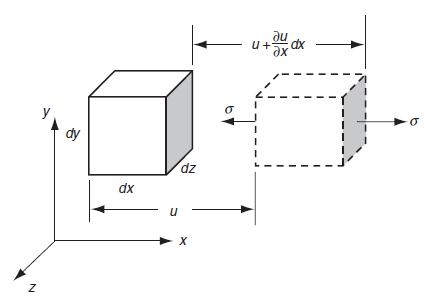
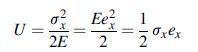
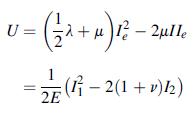
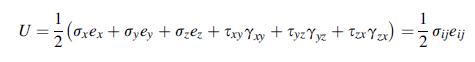
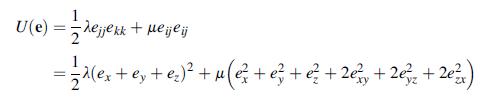
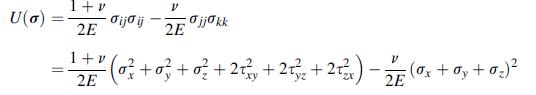
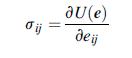
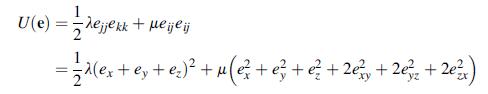
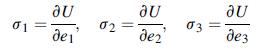
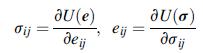
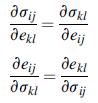
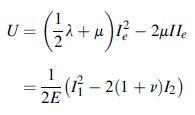
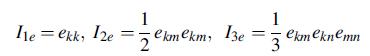
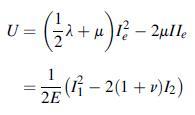
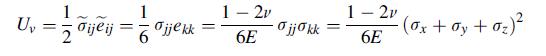
![[( 12 + 362 +672 ) 9 + (*0 0) + (0 ^0) + z(^0 0)] ZI - - -](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1704/9/5/6/273659f91712b3061704956272119.jpg)
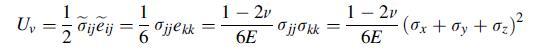
![Ua 12 1 [(ox - 0) + (0 - 0) + (0 0x) + 6 (2xy + y + 1 )]](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1704/9/5/6/369659f91d195ff21704956368559.jpg)
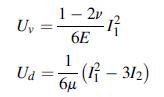
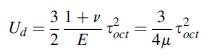
![Ua 121 [(x a) + (ay 0) + (0 0x) + 6(y + 3 +2)] -](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1704/9/5/6/537659f9279ad1e31704956536642.jpg)
![N = 0 oct -3 (0 + 0 +03) = 30kk = 3/1 S = Toct = 1/[(0-0) + (0-03) + (03-0) ] /2 = (217-612) /2](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1704/9/5/6/577659f92a1ec6101704956576888.jpg)
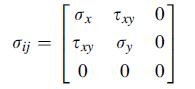
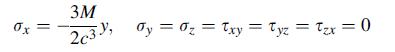
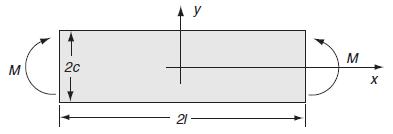
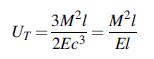
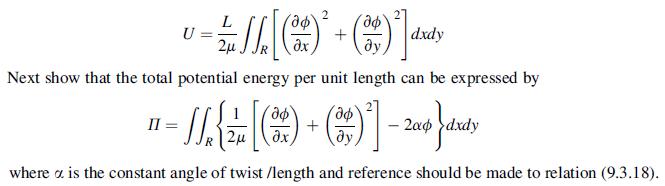
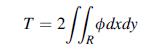
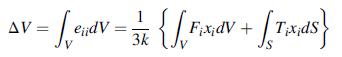
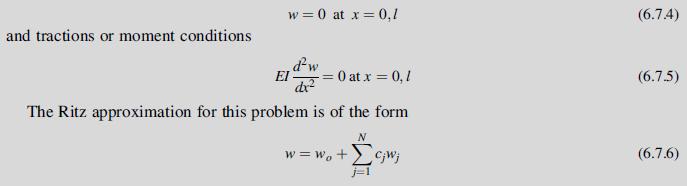
![2 dw II = = [[5/7 (2) - 9ow]dx dx 2 N L'H * ( = 0-1)-2-j0j +1)xj-] N -90cx (1-x) dx - 39/4](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1704/9/5/7/621659f96b541f301704957619668.jpg)
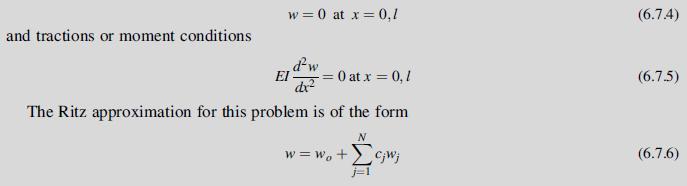
![2 dw II = = [[#1 (22) - 9ow]dx dx 2 N L'H * S ( = N 0-1)-2-j0j +1)xj-] - 90 cx (1-x) dx](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1704/9/5/7/859659f97a34cee41704957858210.jpg)
![ex ey v = 1 + ((1 - v)ox - vy] E exy 1+v E -[(1 - v)oy - vox] 1 + v E -Txy](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1704/9/6/0/361659fa169043141704960359877.jpg)