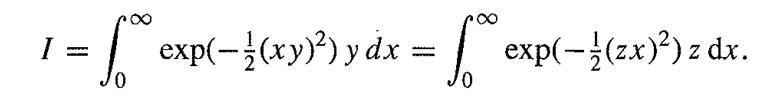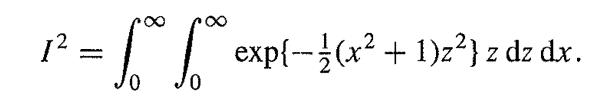![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


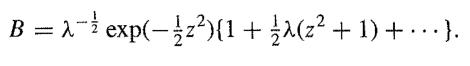
![P(x) = {2(y +)} exp[-(x 00)/(y + p)].](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/9/3/7/7836562403754b9b1700937776800.jpg)
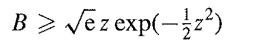
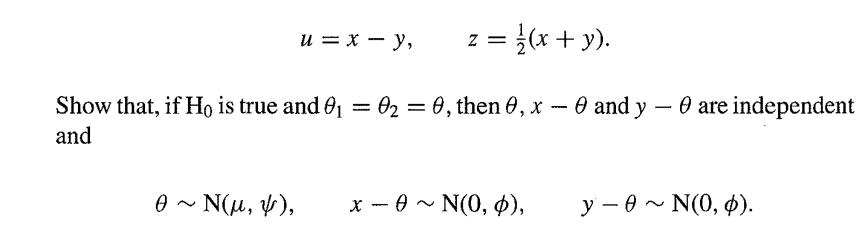
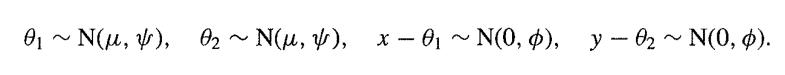
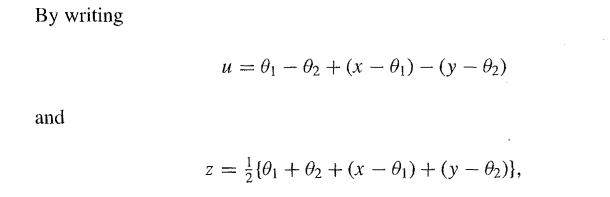
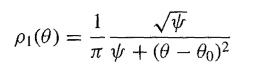
![g'(x) = {n[(x){1+(x)}].](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/9/2/9/21765621ec11943c1700929210947.jpg)
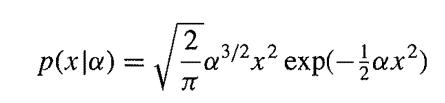
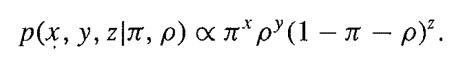
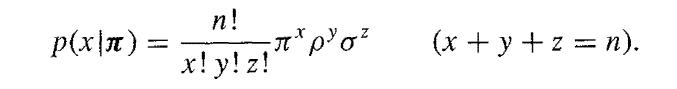
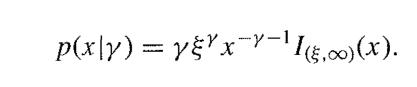
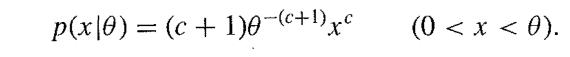
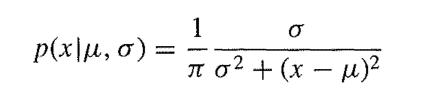
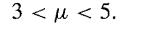
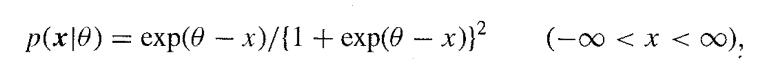

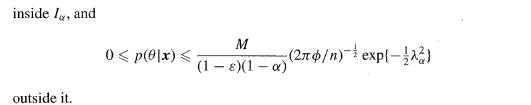
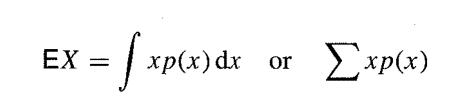
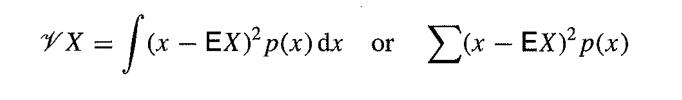
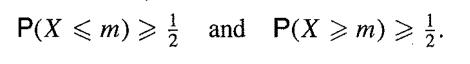
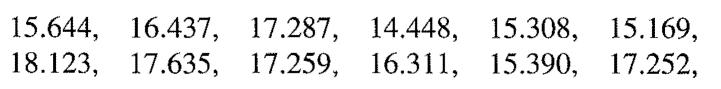
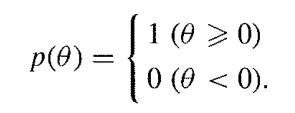
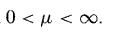
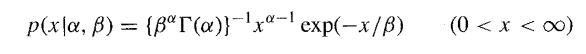
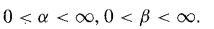
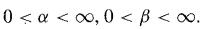
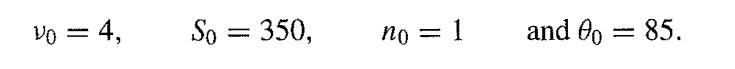
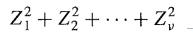
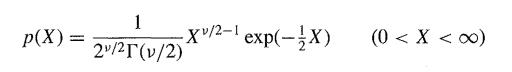
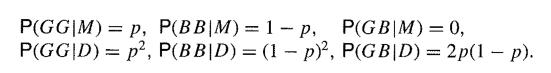


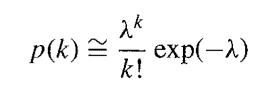
![M = max(x, x2, ..., Xn] and m= min{x, x2, ..., Xn}](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/9/1/1/9946561db7a612911700911987886.jpg)
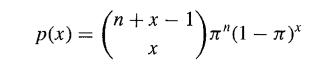
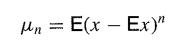
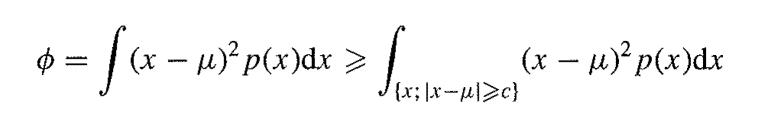
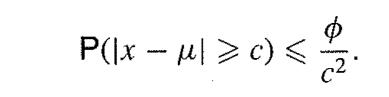
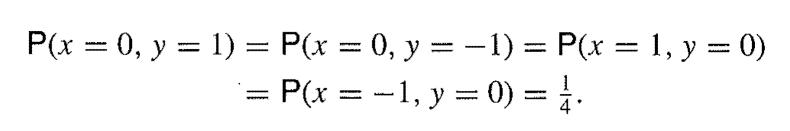
![-1 p(x, y) = {2 (1- p)] ' exp{- (x 2pxy + y)/(1 p)}. .](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/9/2/3/112656206e8440431700923107095.jpg)
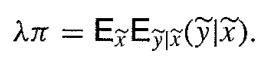
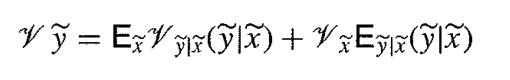
![J = ] = exp(-1/z) dz](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/9/2/3/634656208f23d0111700923628090.jpg)