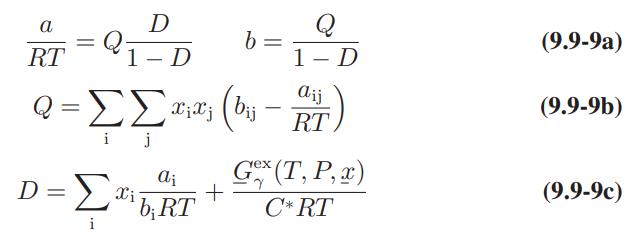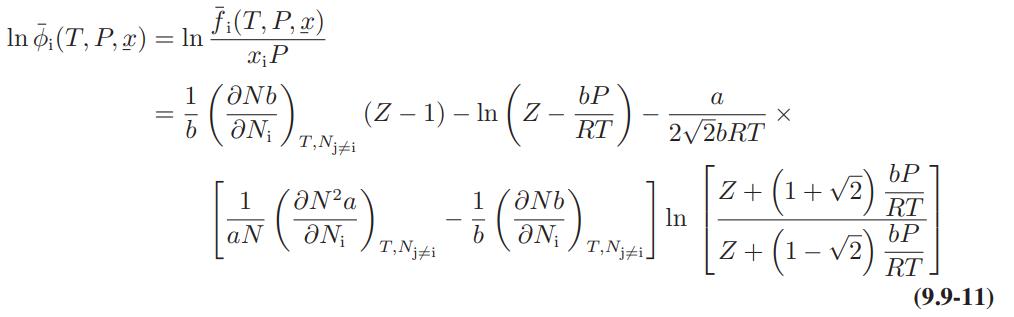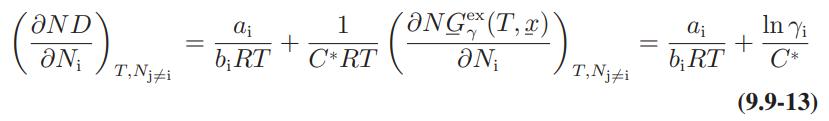![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()



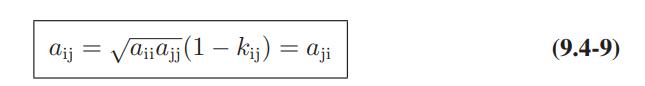
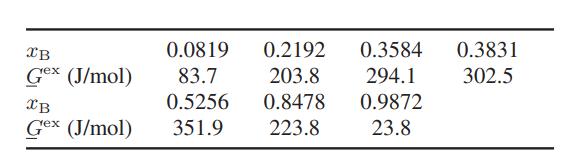
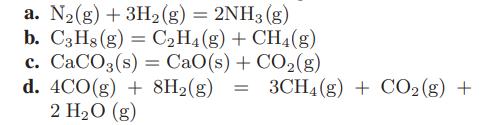
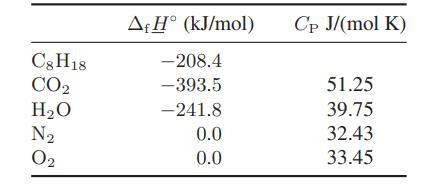
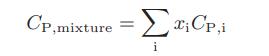
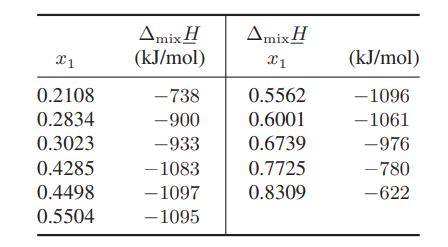
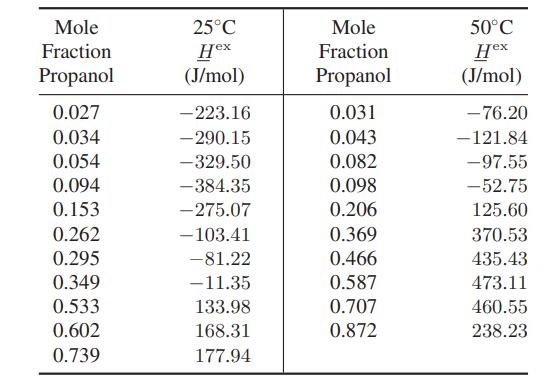
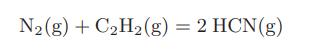
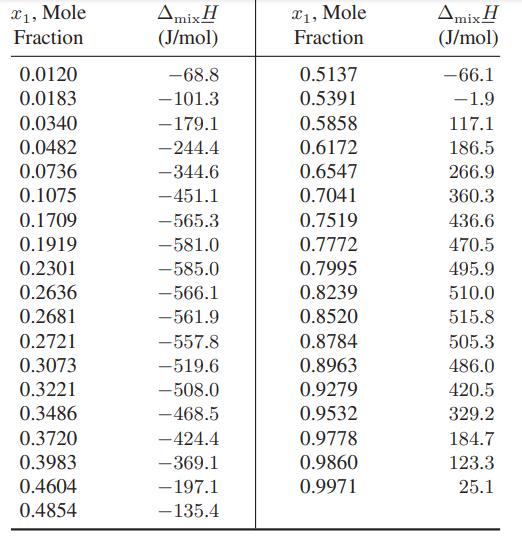
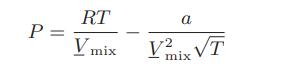
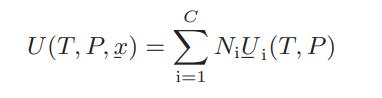

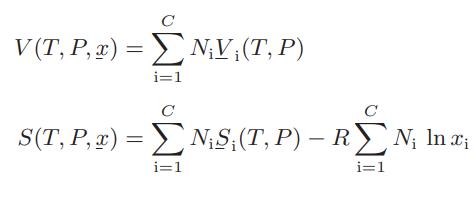
![Amix V(x) = x1x2 [-1.026 +0.220(x - x)]](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/1/1/5/5506555b45eea7931700115549405.jpg)
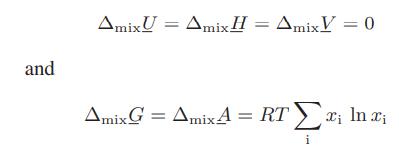
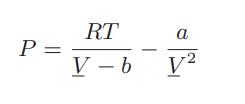
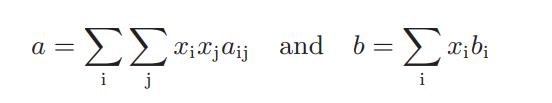
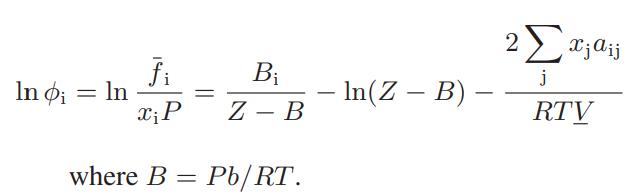
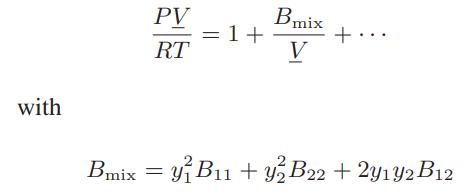
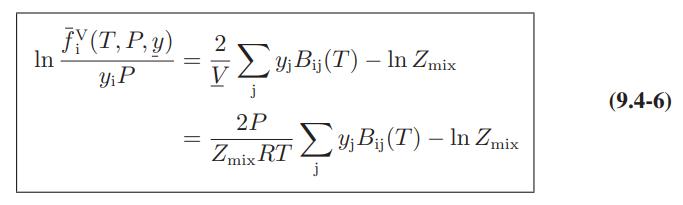
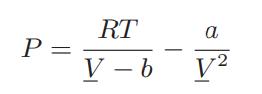
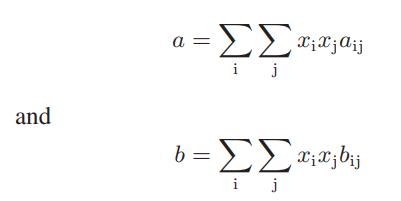
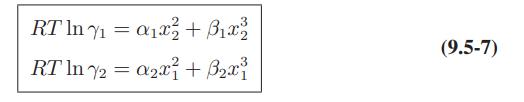
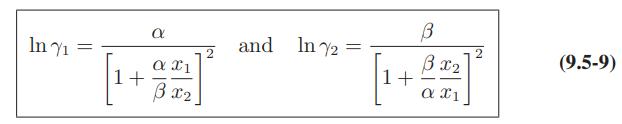

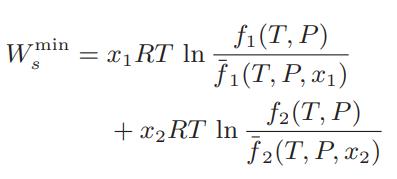
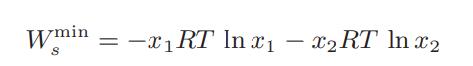
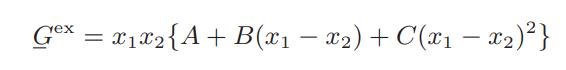
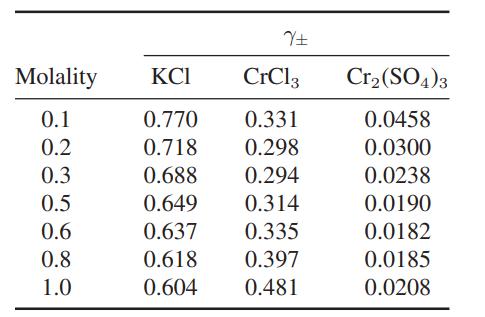

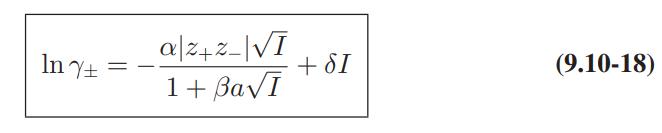
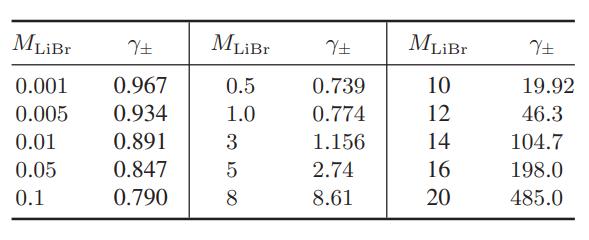


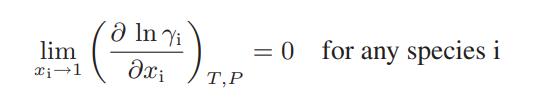
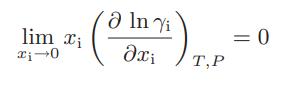
![where Gex == - RT ;; ; 1n ;4;; i=l = (Xij- Aii) ] exp RT](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/1/3/1/0246555f0d0528091700131023749.jpg)

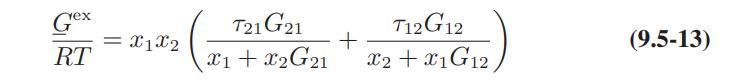
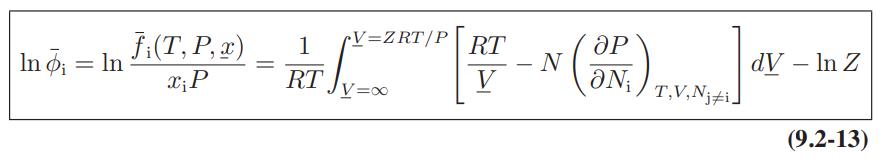
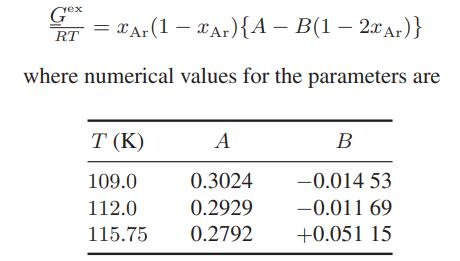
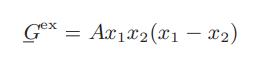
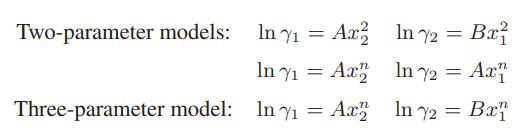
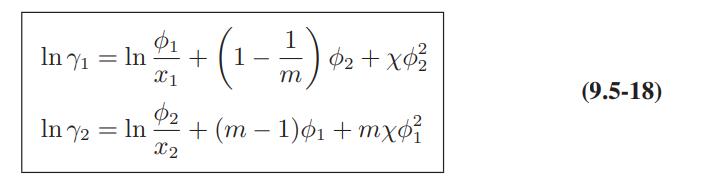
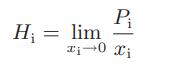
![ABOS [] (* (9.9-8)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/1/3/2/1386555f52a615071700132137814.jpg)