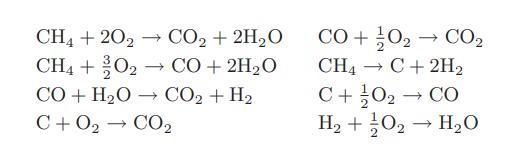![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()




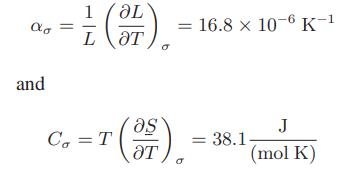
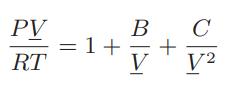
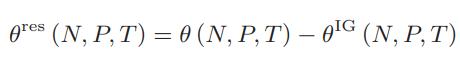

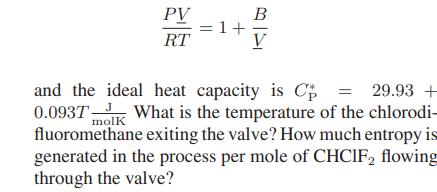
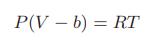
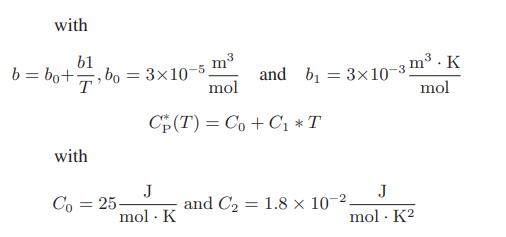
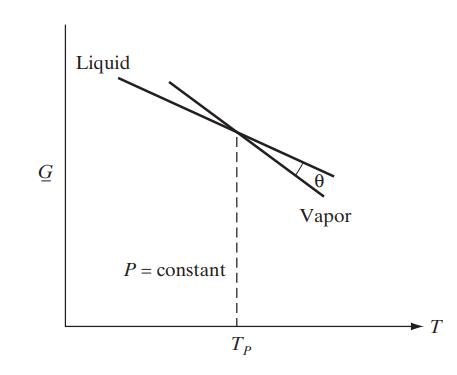
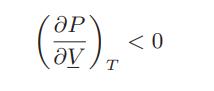

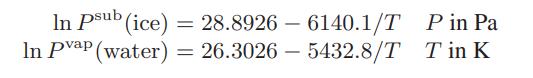
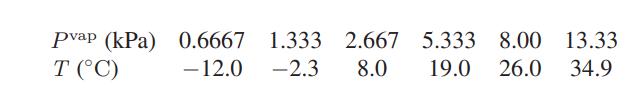
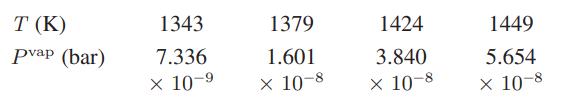
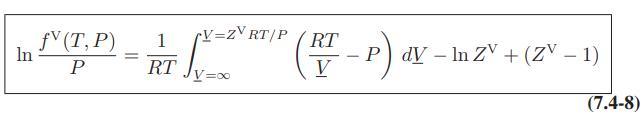
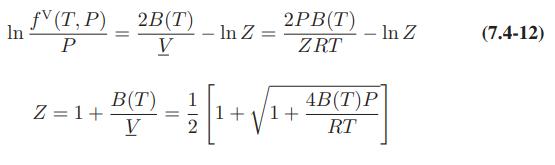
![[P+ 2] . an V CO a = 3.640 L atm / mol V-nb = nRT](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/0/3/0/153655466c90204b1700030022871.jpg)
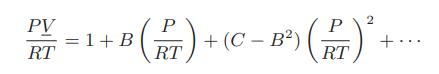
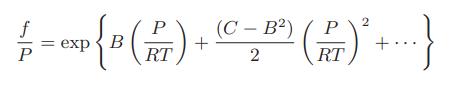
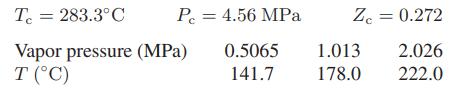
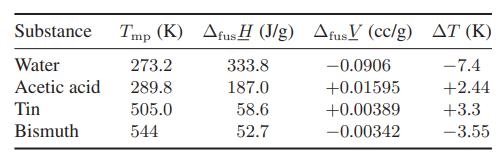
![H - HIG H HIG [(7) -("7").] Te Te AvapH = Tc sat vap sat liq](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/0/3/1/35465546b7a0c9411700031350139.jpg)
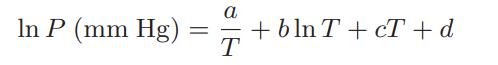
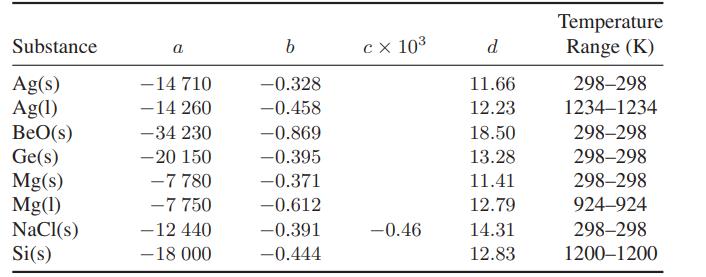
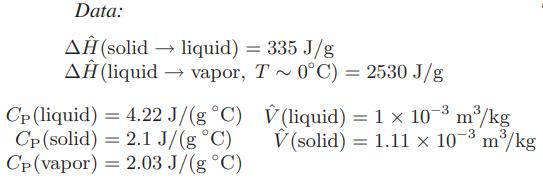

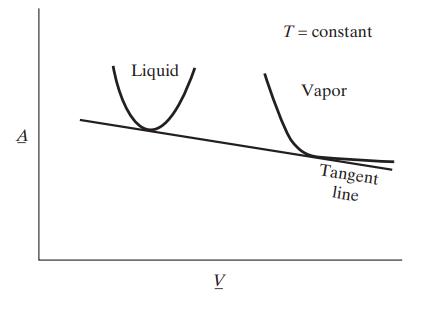
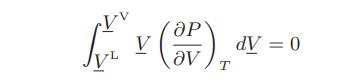
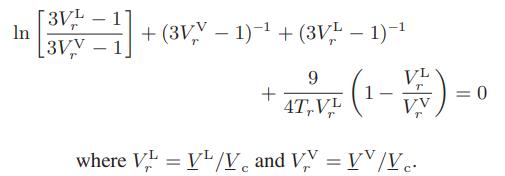
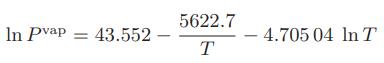
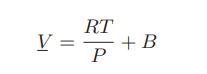
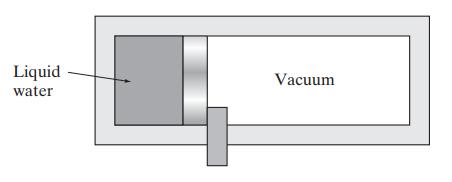
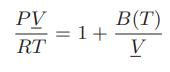
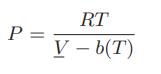

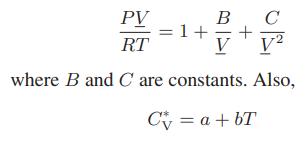
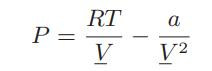
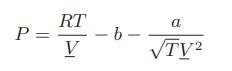
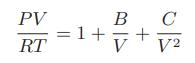

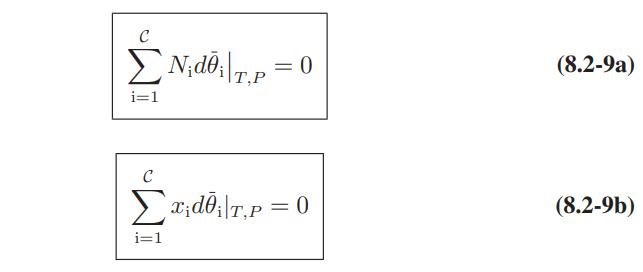
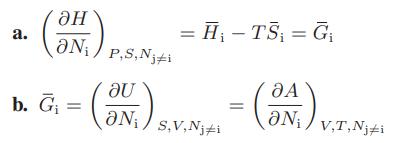

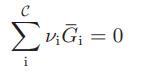
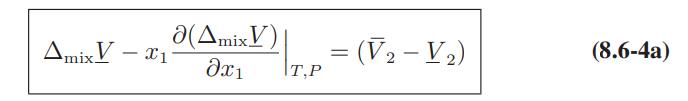
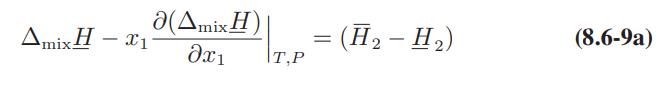

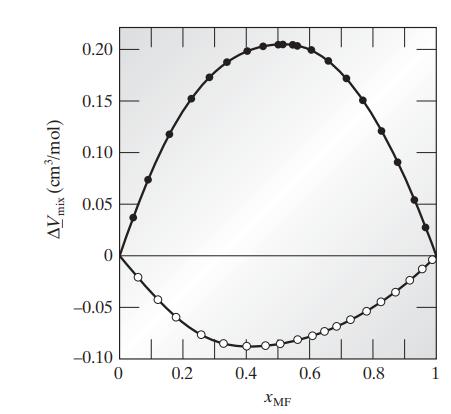
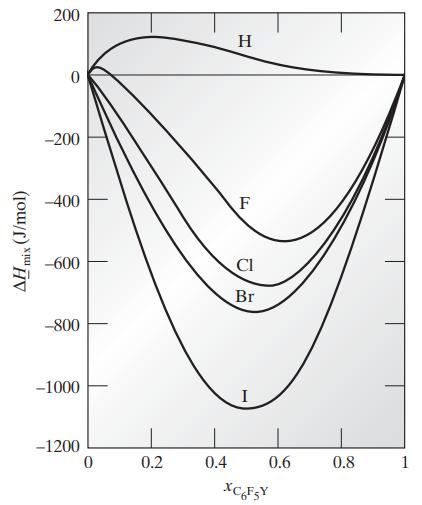
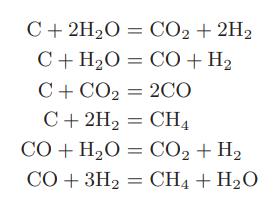
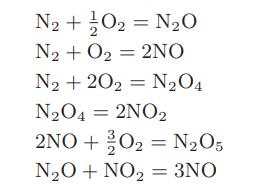
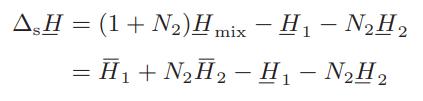
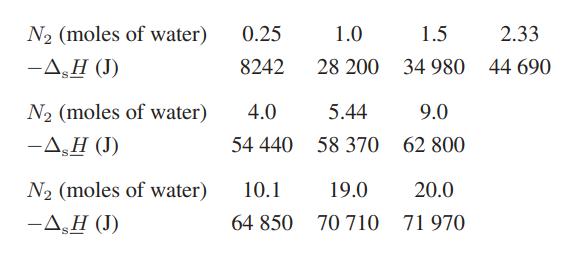
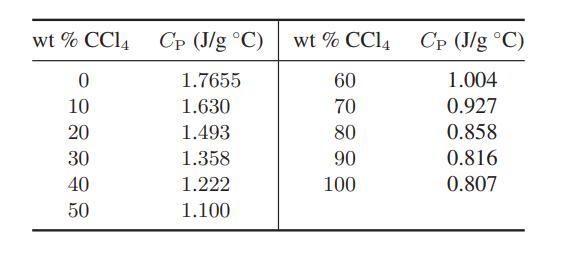
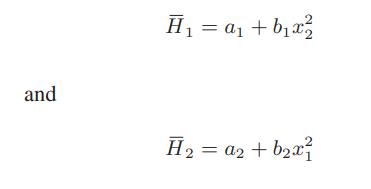
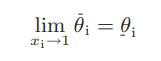
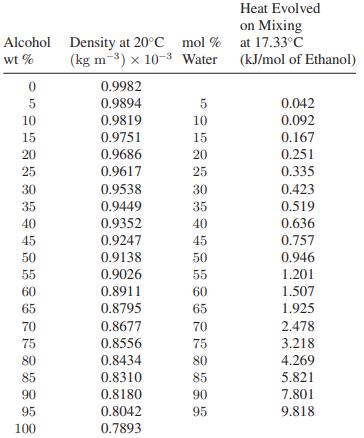
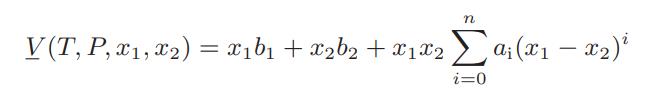
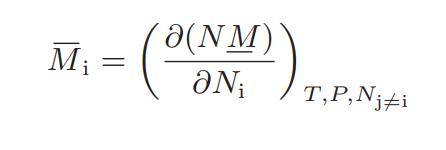
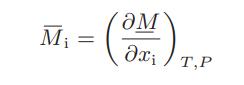
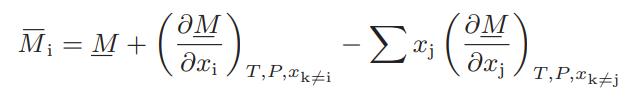

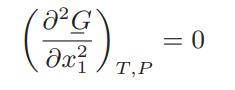
![Hmix - [BHB + (1 - XB)HEA] = XB(1 - XB) {1418 - 482.4(1 - 2X) +187.4(1 - 2xB)}](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/1/1/2/6166555a8e8086fe1700112613280.jpg)
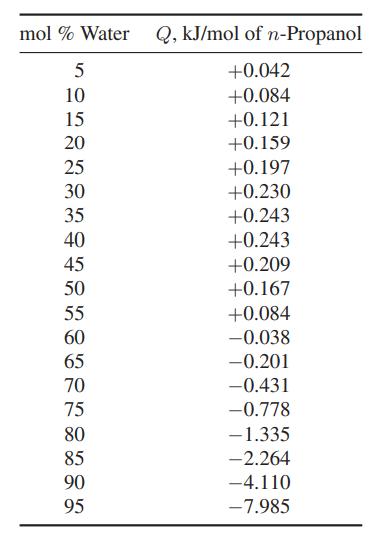
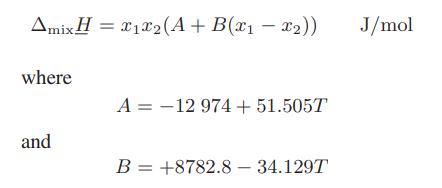
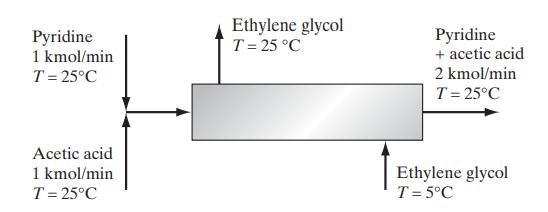
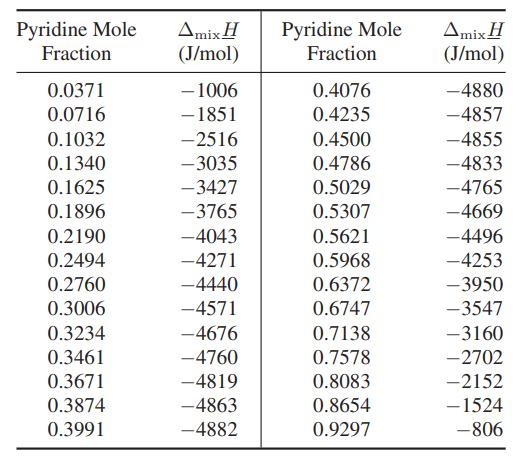
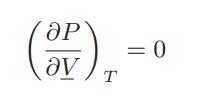
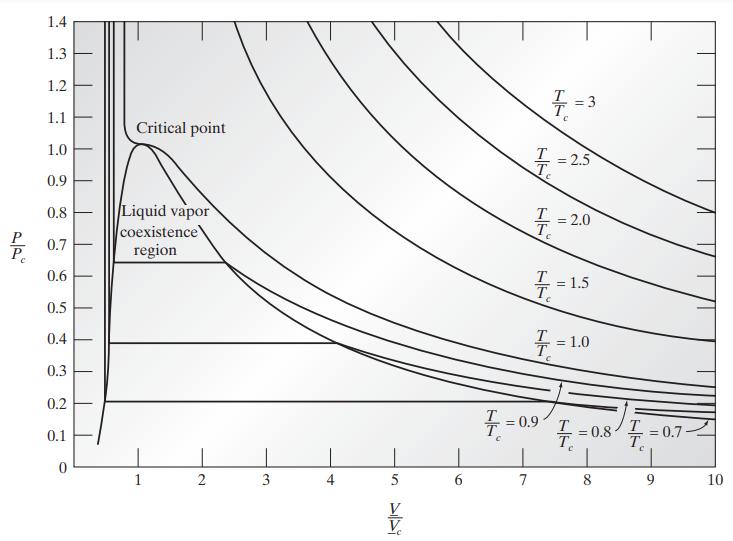
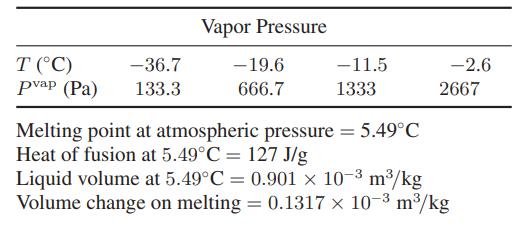
![and T T along phase transition curve along phase transition curve - I T r[(@); - ()"] - P I [(x), P I](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/0/2/8/49765546051b60651700028491537.jpg)