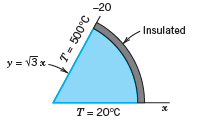
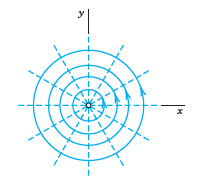
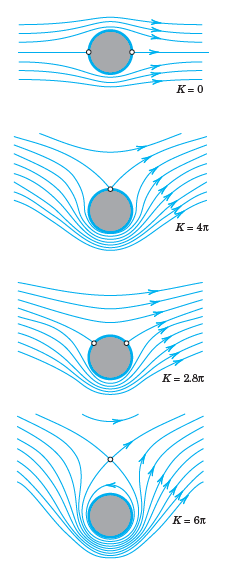
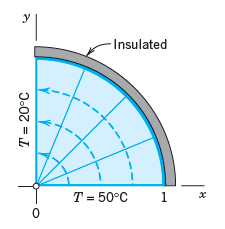
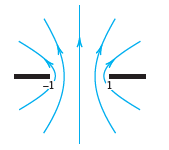
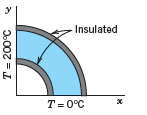
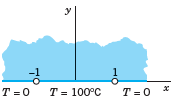
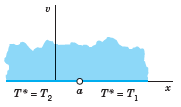
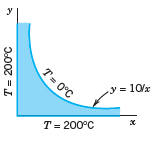
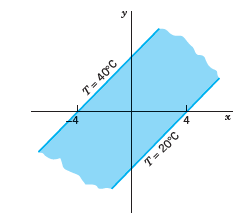
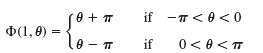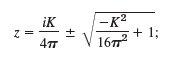![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


![А: Го — [x (0), у (0)] 3D [xо. Уol. B: r1 = [x(1), y(1)] = [x1, yı] Vo = [x'(0), y'(0)] — [x6. уб1. V1 = [r](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/1/2/5/1485c18bd1c3aae71545107728742.jpg)