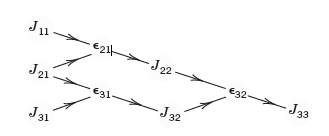
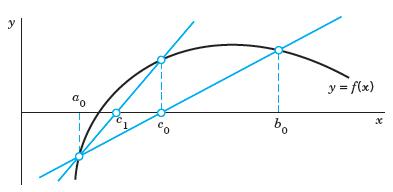
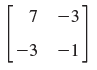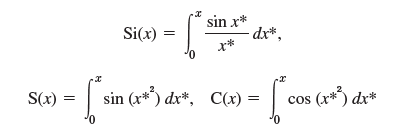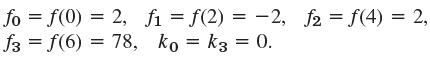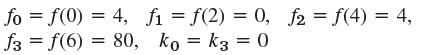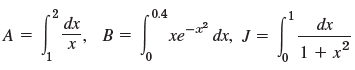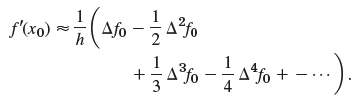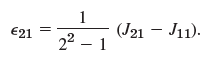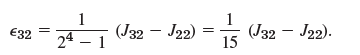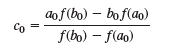![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


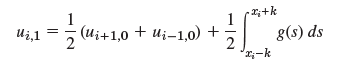

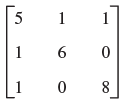

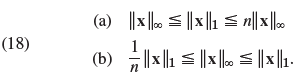
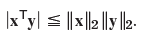
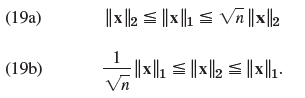
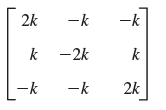
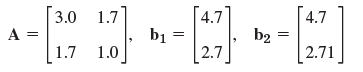
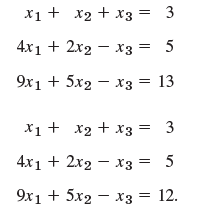
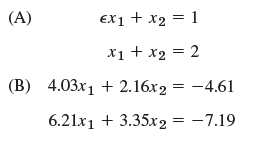
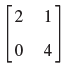

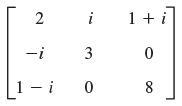

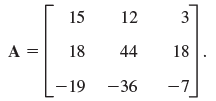
![[0.6 0.8] A 0.8 -0.6](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/2/1/8/5435c1a29ef12c6d1545147405203.jpg)