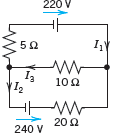
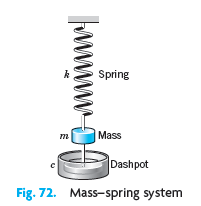
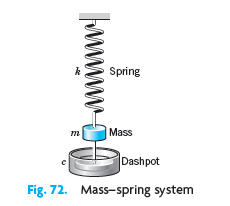
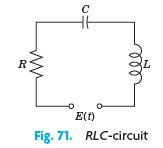
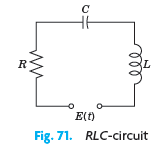
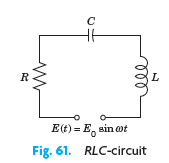
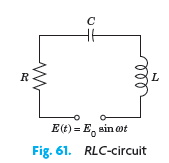
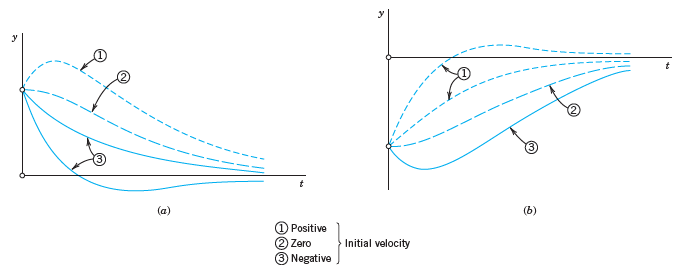
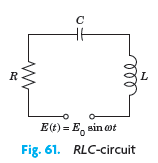
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


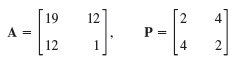
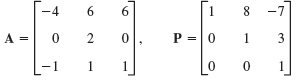
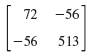
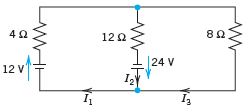
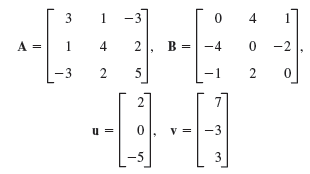
![Let 4 -2 3 -3 A =-2 1 B = -3 6. 1 2 2 -2 1. a = [1 -2 0], 0), b = 3 2 -2](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1542/3/8/9/7455beefff102c0c1542259338654.jpg)


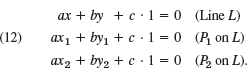
![х — х] у — У X1 - X2 У1 — У2'](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1542/7/0/5/2805bf3d08072d321542294411156.jpg)