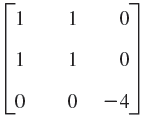![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


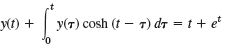
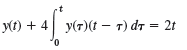
![ат -[(x² – 1)*]. 1)](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1542/1/0/1/5105bea9a069498f1542030080382.jpg)