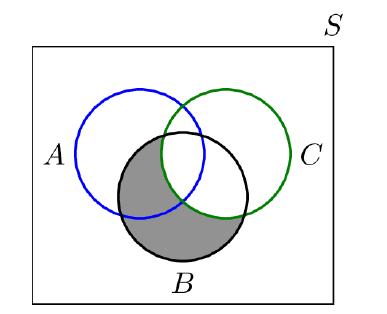
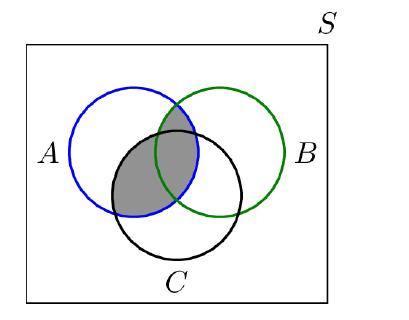
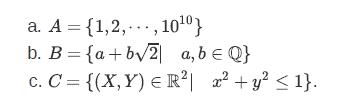![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


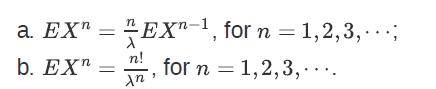
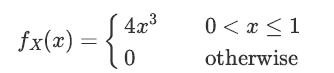
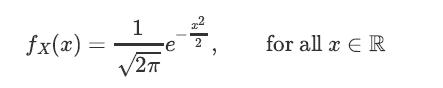
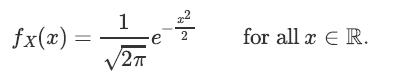
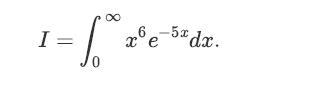
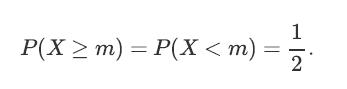
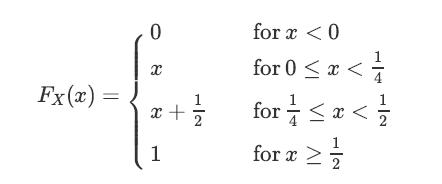
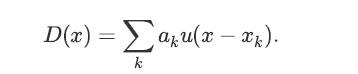
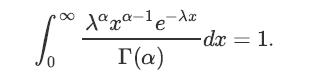
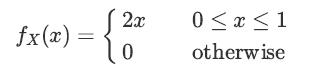
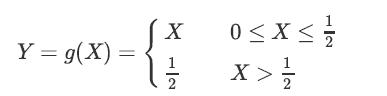
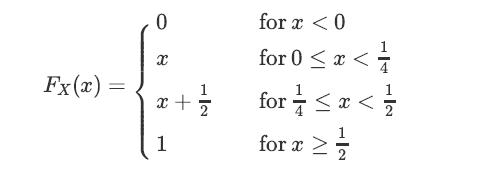
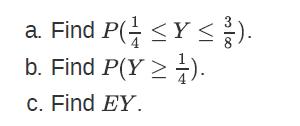
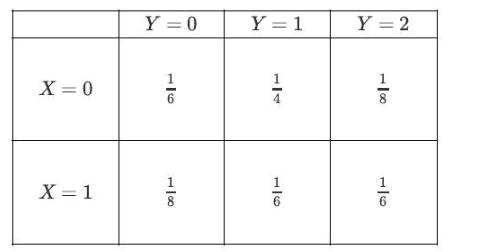
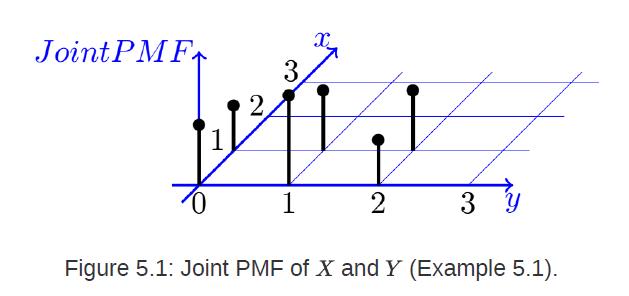
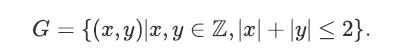
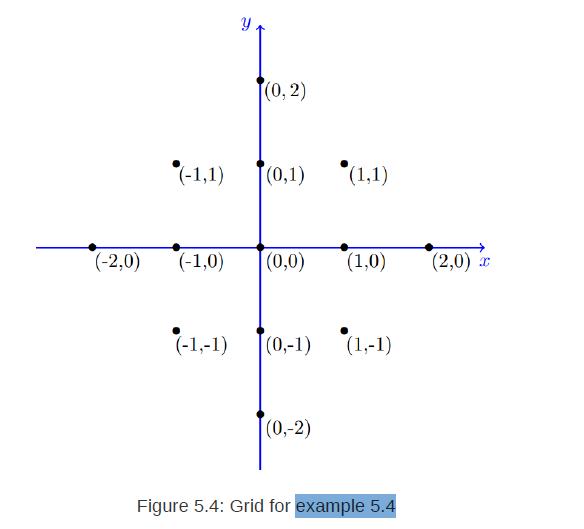
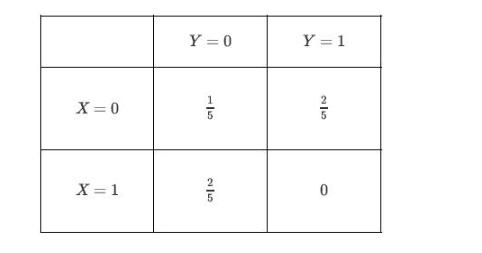
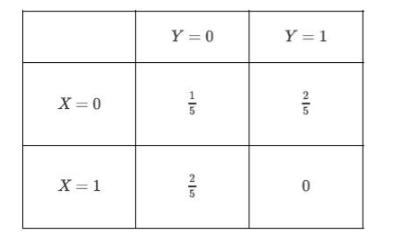
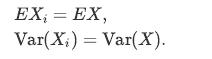
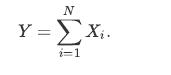
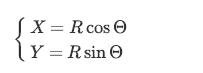
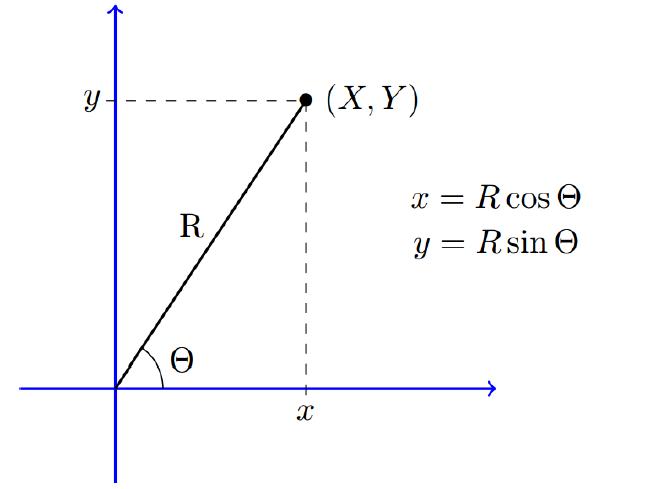
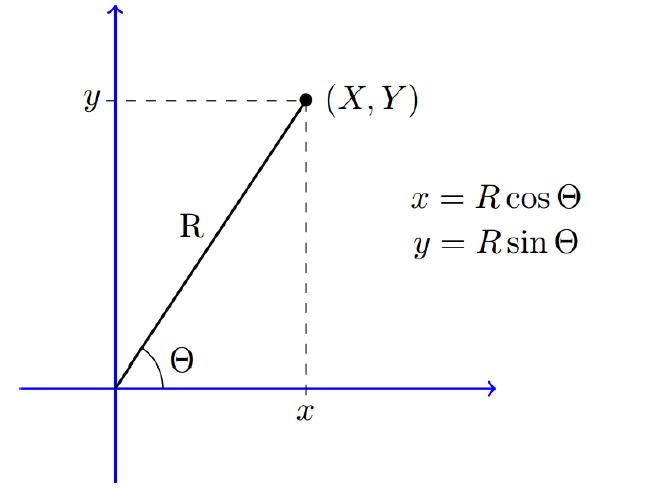
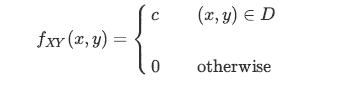
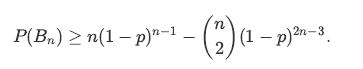
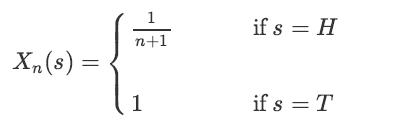
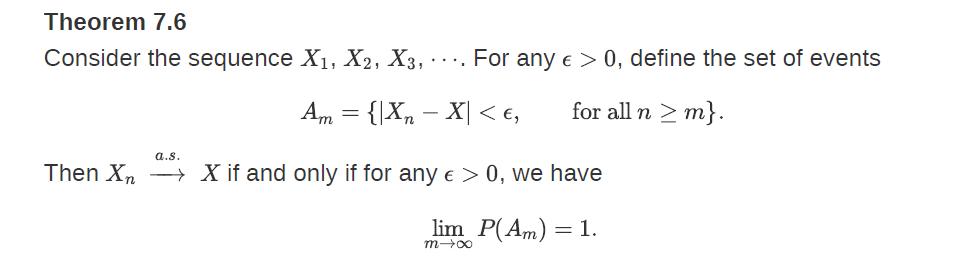
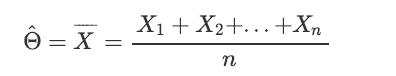
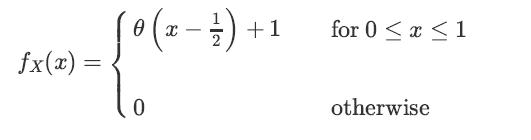
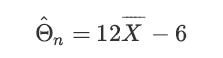
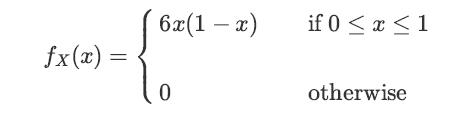
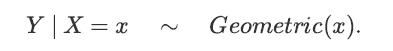
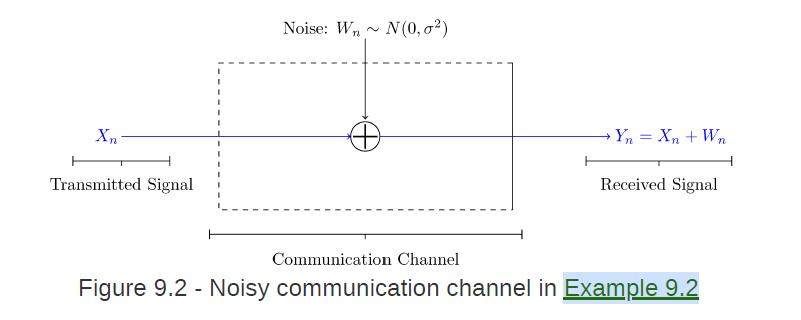
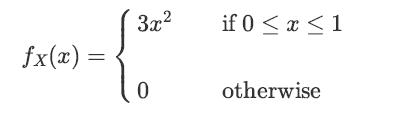
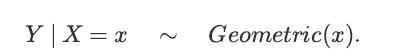
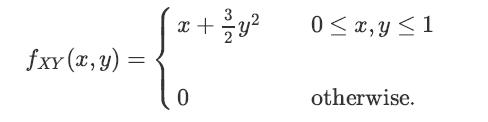
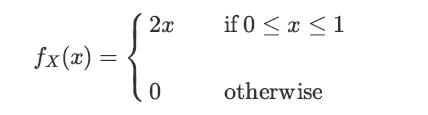
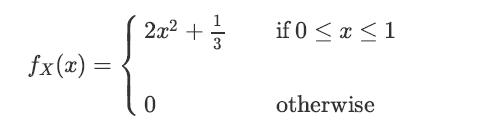
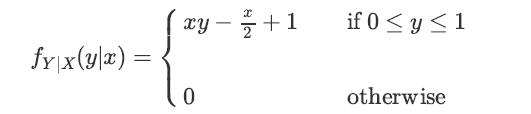
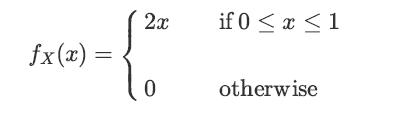
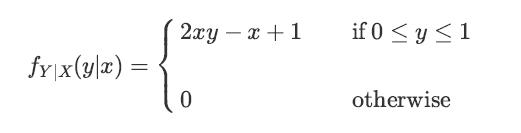
![XL = CXYCY (Y - E[Y]) + E[X].](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1698/3/8/2/586653b42fa5dcc41698382585572.jpg)
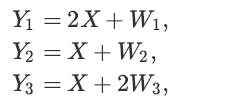
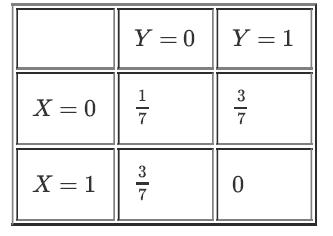
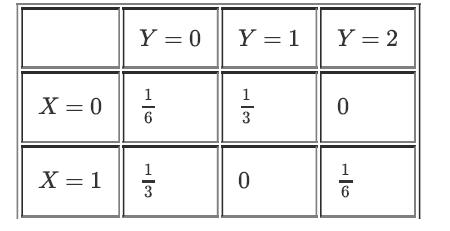
![A]. [xx] = 0 Y- G](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1698/3/8/9/455653b5dcf972781698389453241.jpg)
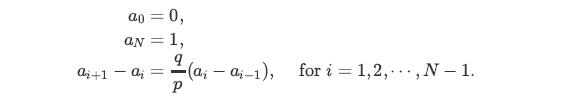
![2 i-17 9 = [ + + ( ) + + + ( ) ^ ] - 9 P P P a, for i=1,2,..., N.](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1698/3/9/3/888653b6f209d9e31698393883997.jpg)
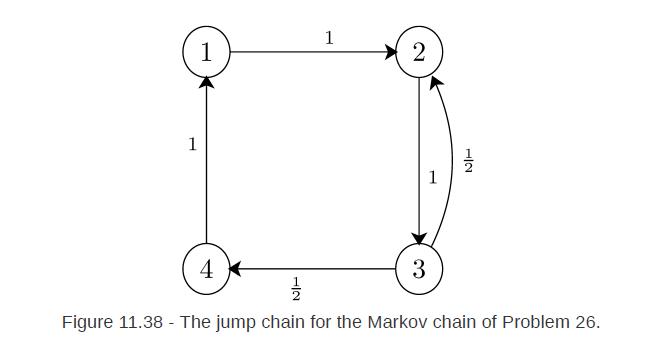
![a. Find the stationary distribution of the jump chain = [1,2,3,4]. b. Using , find the stationary](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1698/3/9/3/968653b6f700940f1698393962897.jpg)
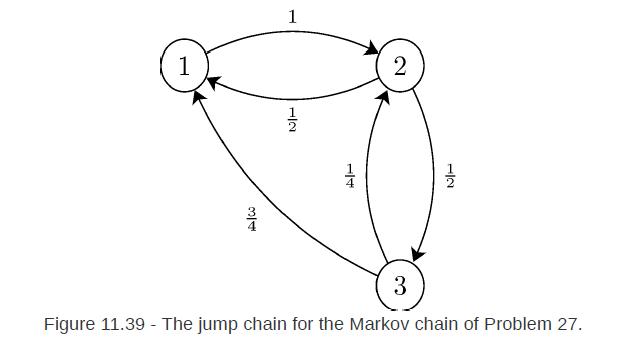
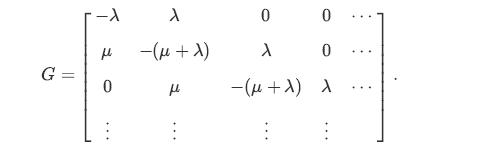

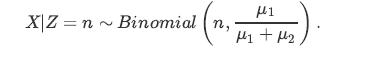
![P(Ta t)=21-0 a (+7)] t](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1698/3/9/4/413653b712dbd55b1698394413371.jpg)