![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


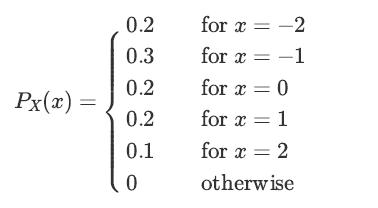
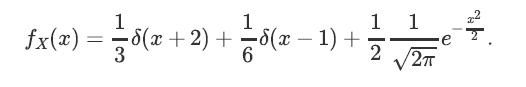


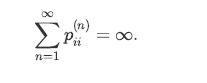
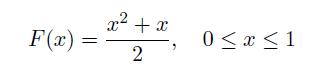
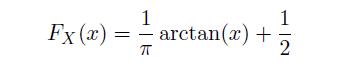
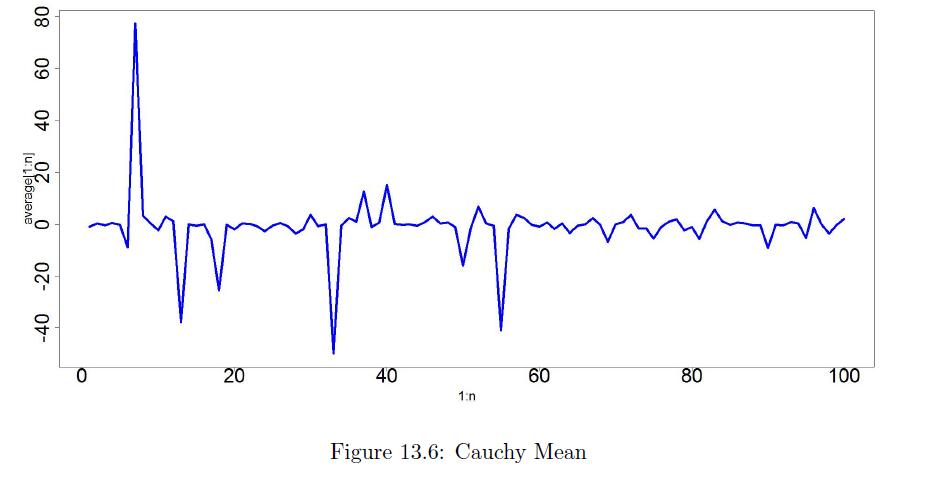
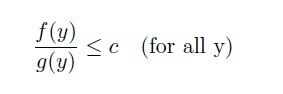
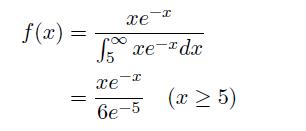
![Pr\x(ya) = (") x(1 x x(1-x)-y, for x = [0, 1], y = {0, 1,...,n},](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1698/3/8/2/965653b44759b31d1698382963119.jpg)
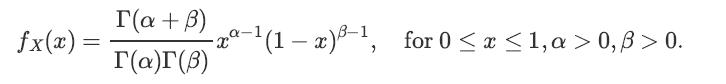
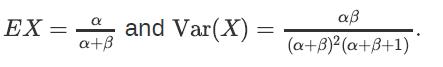
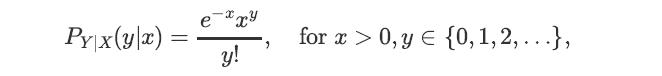
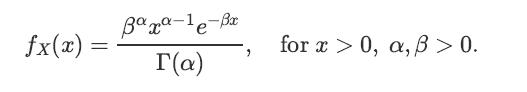
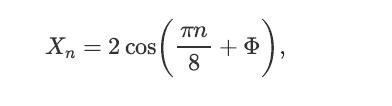
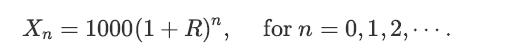
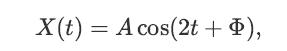
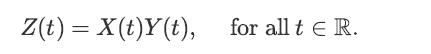
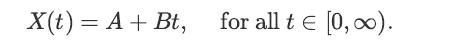
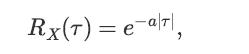
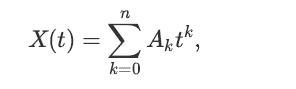
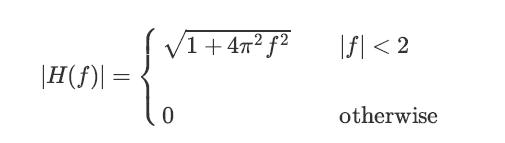
![x(t) = E[X(t)] = E[X, (t)] + jE[Xi(t)] = x, (t) + jux, (t); Rx (t1, t2) E[X(t)X* (t)] = = E [(Xr(t) +](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1698/3/8/7/311653b556f778551698387309627.jpg)
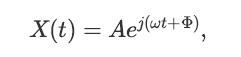
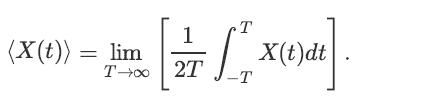
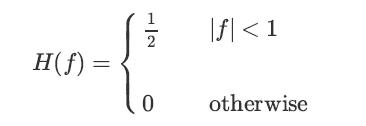
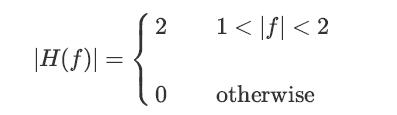
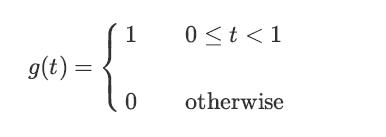
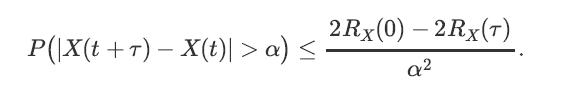
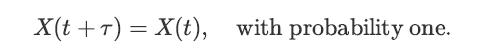
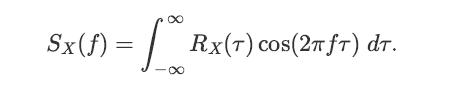
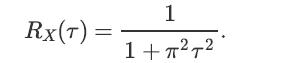
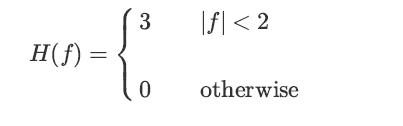
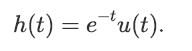
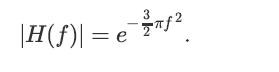
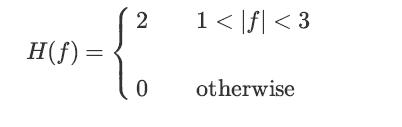
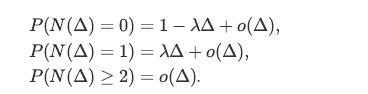
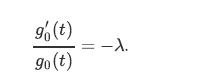
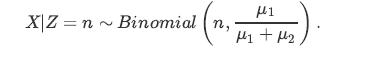
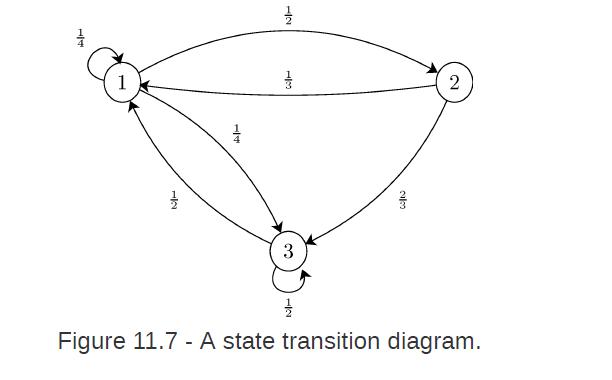
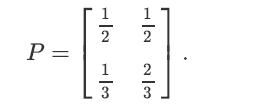
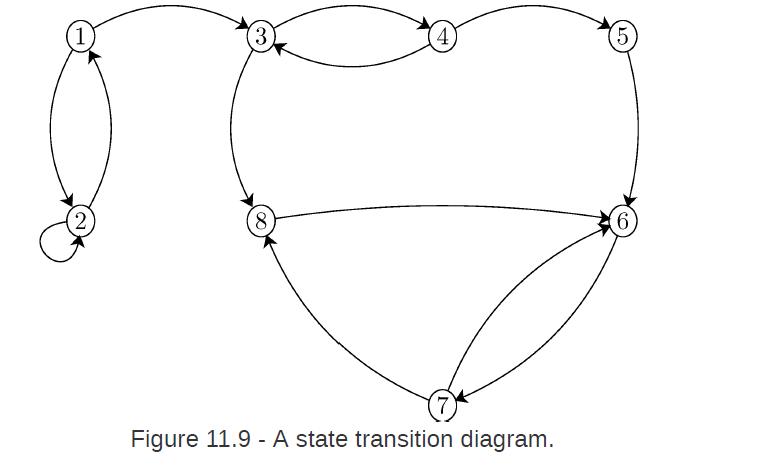
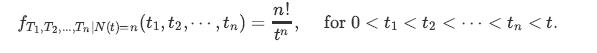
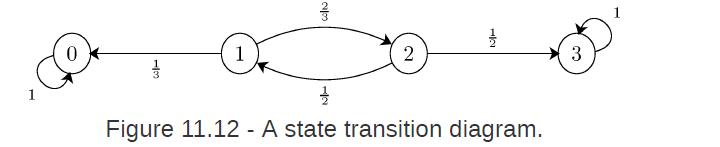
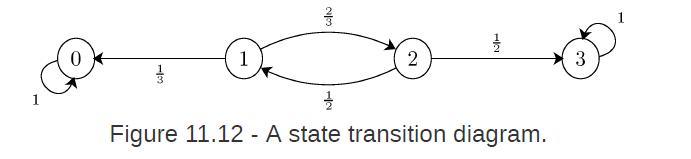
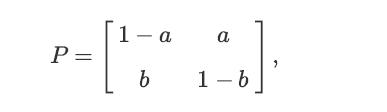
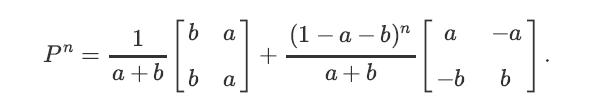
![lim Pn = pn n 1 b +[a] a+b b](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1698/3/8/8/574653b5a5e86cdd1698388571794.jpg)
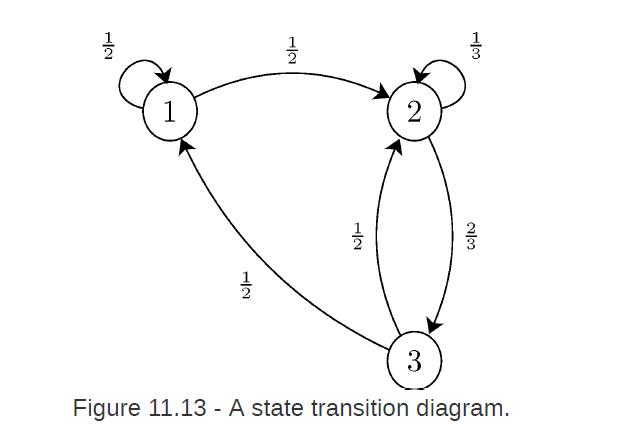
![P = 1-a a :.]. b 1-b](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1698/3/8/8/608653b5a8038d481698388606361.jpg)
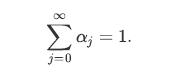
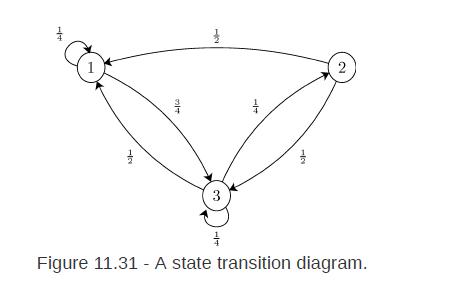
![P = 1-a b a %.]. 1-b](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1698/3/8/8/942653b5bce87d671698388941030.jpg)