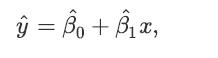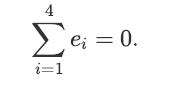![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


![fx(i)(x) = = n! fx(x) [Fx(x)] [1 - Fx(z)]". (i-1)! (ni)! *](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1698/3/0/7/434653a1d6a789341698307432727.jpg)

![n Fxs) (x) = (7) [Fx(2)] * [1 Fx(x)]*-*. (i) k k=i](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1698/3/0/7/302653a1ce620bfc1698307300474.jpg)
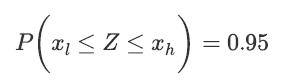
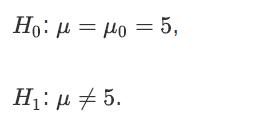
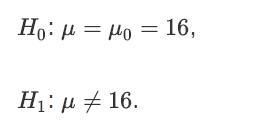
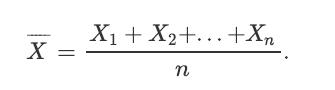
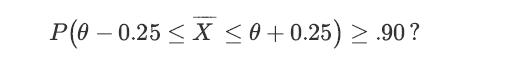
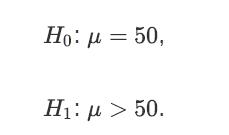
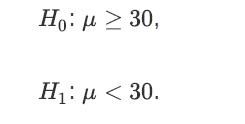
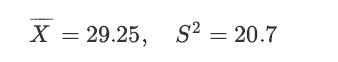
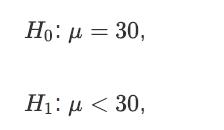
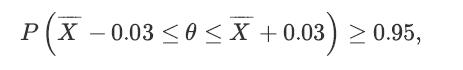
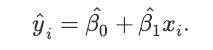
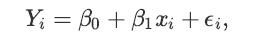
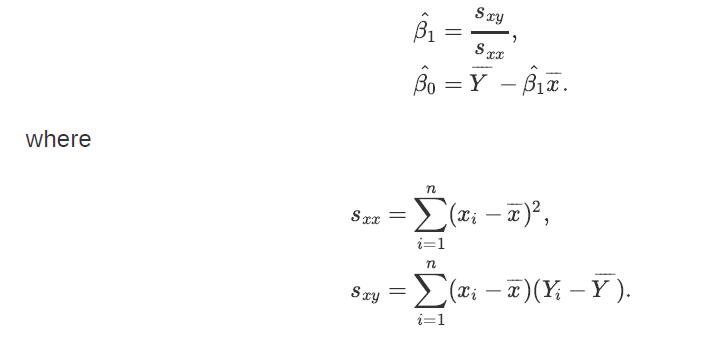
![a. Show that B is a normal random variable. b. Show that is an unbiased estimator of 3, i.e., E[81] =B. c.](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1698/3/0/8/314653a20da633eb1698308312683.jpg)
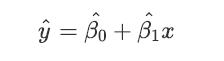
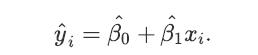

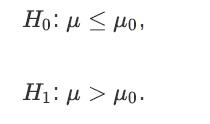

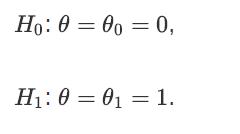

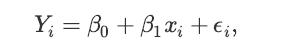
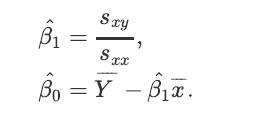
![a. Show that Bo is a normal random variable. b. Show that is an unbiased estimator of Bo, i.e., E[Bo] = Bo.](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1698/3/0/8/364653a210cef9af1698308361990.jpg)