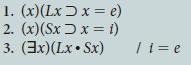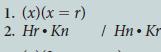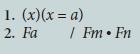![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


![1. (x) [Fx (Gx.x = n)] 2. Gn (3x)(Hx.x = e) Ca 1 Fm He](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1696/4/2/0/064651d50e0e42171696420063667.jpg)
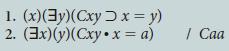
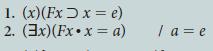
![1. (x) (Px x = a) 2. (x) (x = c] Qx) 3. a = c / (x) (Px Qx)](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1696/4/1/9/416651d4e5899d131696419415307.jpg)