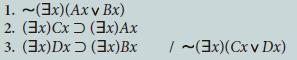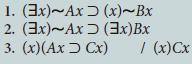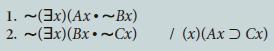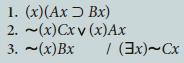![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


![1. (3x)(Ax Bx) 2. (3x)(CxBx) 3. (x)(Ax Cx) / (3x) [(CxBx)~Ax]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1696/3/2/7/970651be9220737f1696327966219.jpg)
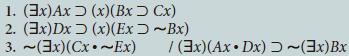
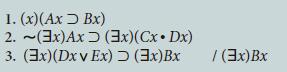
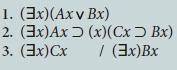
![1. (x) (Ax=Bx) 2. (x)[Ax 3. (3x)Axv (Bx > Cx)] (3x)Bx / (3x)Cx](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1696/3/2/6/072651be1b8824f31696326067626.jpg)
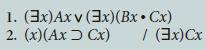
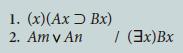
![1. (x)(Ax > Bx) 2. (x) [(AxBx) Cx] / (x)(Ax Cx)](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1696/3/2/0/542651bcc1e15f5e1696320541025.jpg)
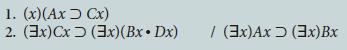
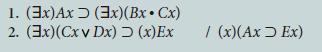
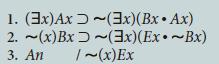
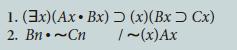
![1. (3x) Ax [(3x)Bxv (x)Cx] 2. (3x)(Ax~Cx) 3. ~(x)Cx [(x)Fx (x)~Bx] /(3x)~Fx](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1696/3/1/9/522651bc8227c1ee1696319521655.jpg)
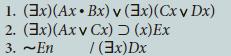
![1. (3x)(AxBx) 2. (x)[(Axv Ex) (Bxv Fx)] 3. ~(x)Dx /(x)(Ex v Ex) (x)(Cx Dx)](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1696/3/1/9/469651bc7ed305521696319468316.jpg)