![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


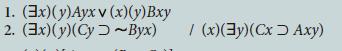
![1. (x)[Ax 2. (x) (BxD Cx) [(y)(By Cy) Dx]} / (x)[Ax (BxDx)]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1696/4/0/2/330651d0b9a9549d1696402330043.jpg)
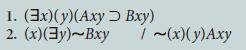
![1. (3x)[Ax. (y)(By Cxy)] 2. (x) (3y)(Ax By) 7 (3x) (y)Cxy](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1696/4/0/1/733651d09450293b1696401732012.jpg)