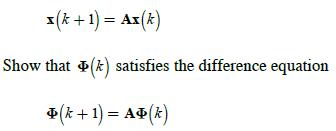![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


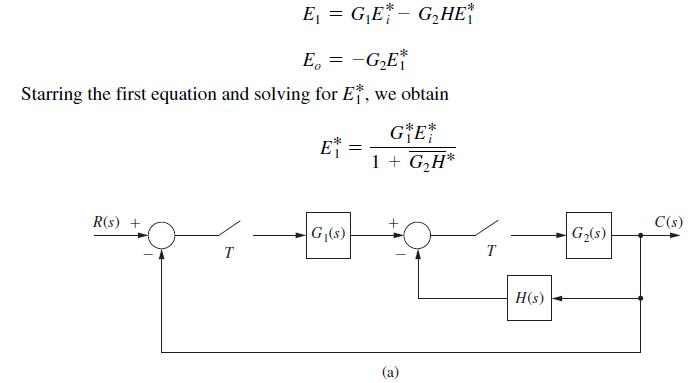
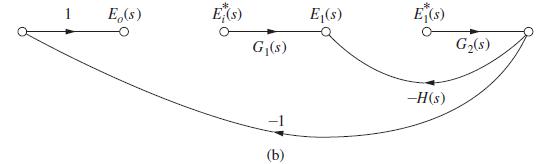
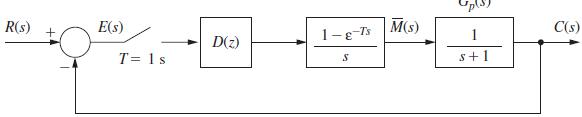


![It is shown in [6] that given the partitioned matrix H = DE F G where each partition is n xn, the determinant](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/6/5/2/63065aa3196bfa541705652629611.jpg)
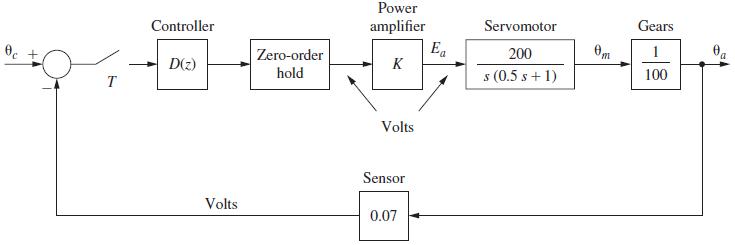
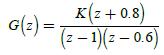

![*[cos akT] = z(z - cos aT) z - 2z cos aT +1 2](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/4/0/2/98965a6626dd50861705402988946.jpg)
![(a) Find the conditions on the parameter a such that [cos akT] is first order (pole-zero cancellation](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/4/0/2/99665a6627434dcc1705402995272.jpg)
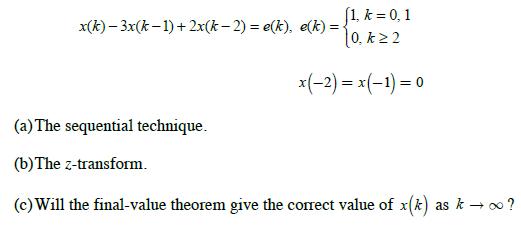
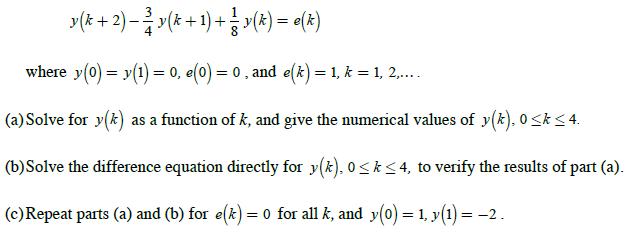



![(d)Find e(k) for k= 0, 1, 2, 3, and 4 if [e(k)] is given by E (2) = 1.98z (2 0.9z+ 0.9)(z 0.8) (2 1.2z +](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/4/0/3/28765a663979f6ca1705403286700.jpg)

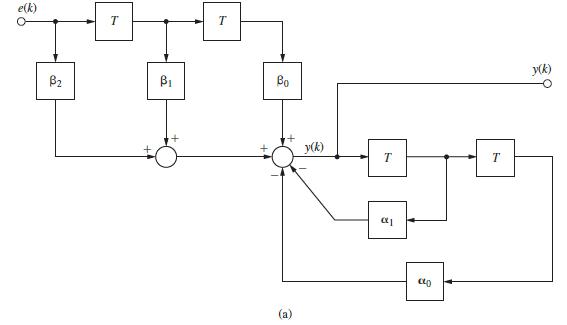
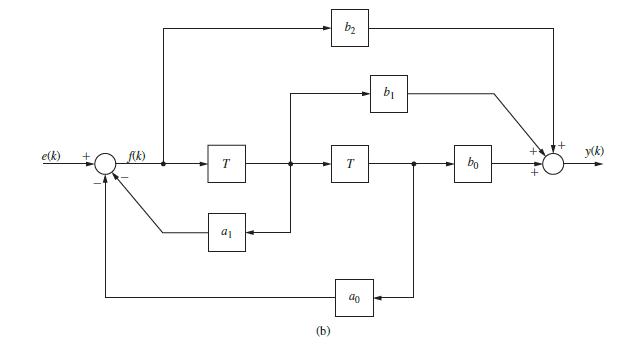

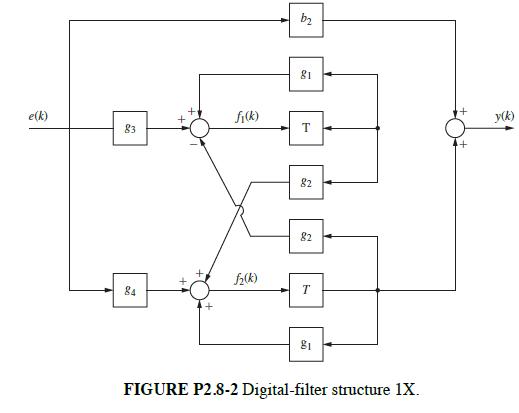


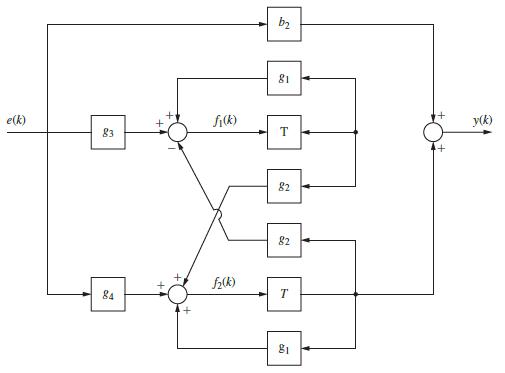
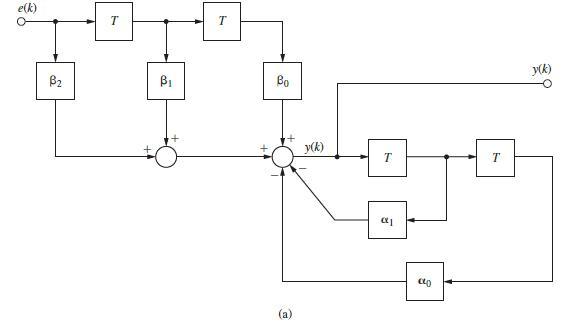
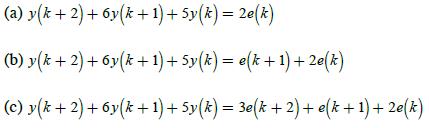
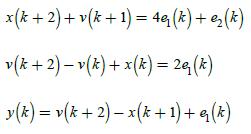
![1 (* + 1) = [ 0 ] (*) + [ (*) 3 y (k)=[-2 1] x(k)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/4/0/4/28365a6677b05d0c1705404282032.jpg)
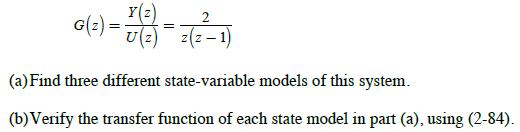
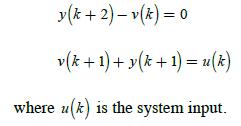


![x(*+1) = 10 0 0.5 (1) + [2]) 1](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/4/0/5/60465a66ca491f921705405603515.jpg)
![y(k)= [1 2]x(k) is excited by the initial conditions x(0)=[-1 2 with u(k) = 0 for all k.](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/4/0/5/64565a66ccdae31f1705405644684.jpg)
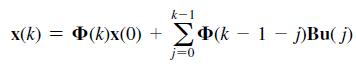
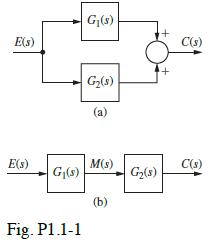
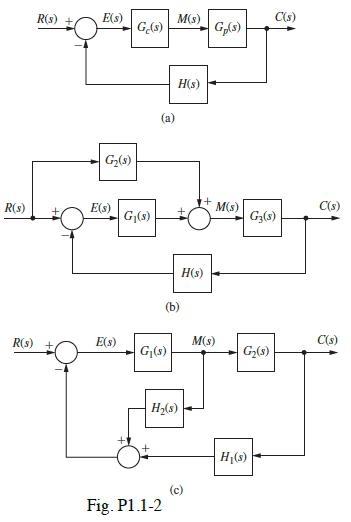
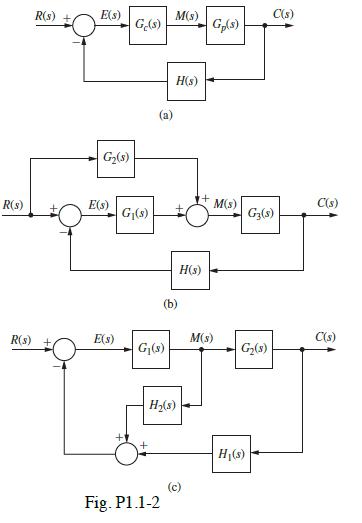
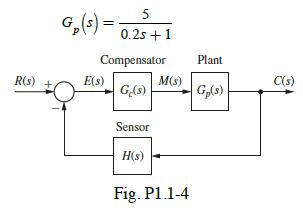
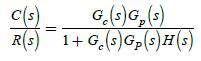
![H(s) = 1 For part (e), recall that the transfer-function underdamped pole term [(s+ a) + b] yields a time =](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/3/9/9/56365a6550b92cfd1705399562140.jpg)
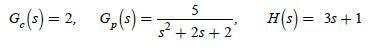
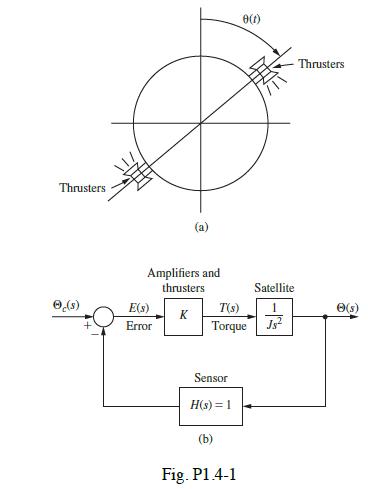
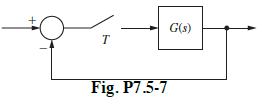
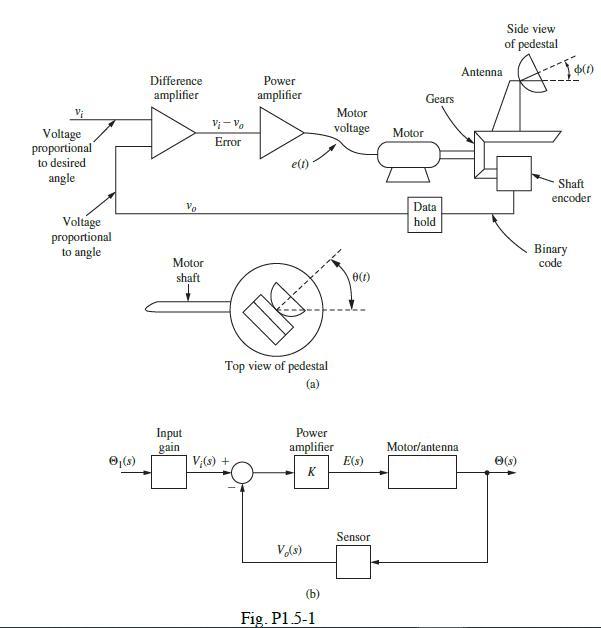
![(a) Derive the transfer function (s)/(s), where e(t) = [0(s)] is the commanded attitude angle. L (b) The](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/3/9/9/70865a6559ce9ed51705399708042.jpg)
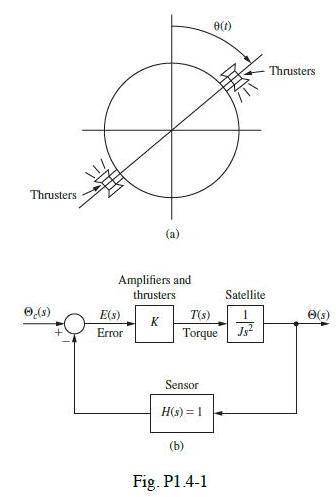
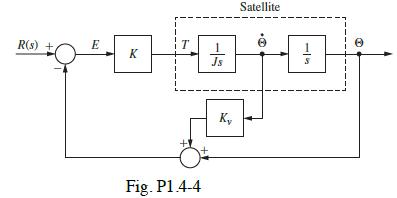


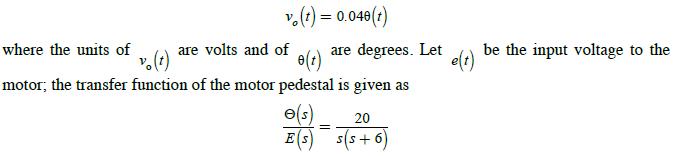
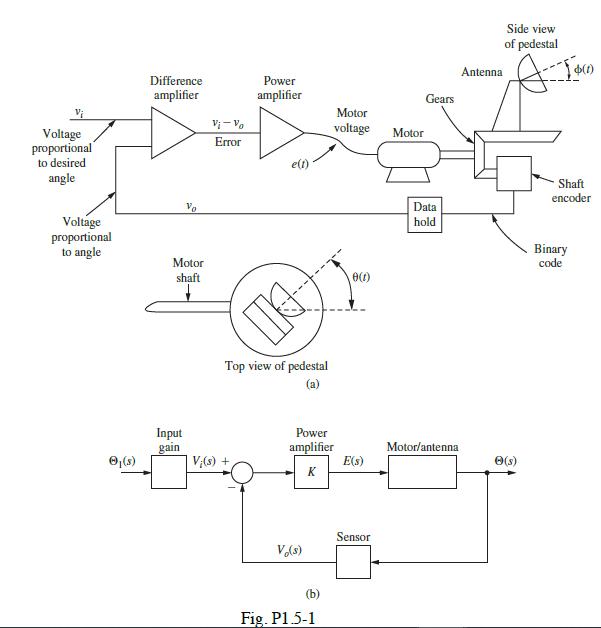
![(a) With the system open loop [.() is always zero], a unit step function of voltage is applied to the motor](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/4/0/0/31465a657fa91c781705400313641.jpg)

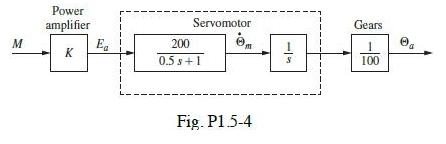

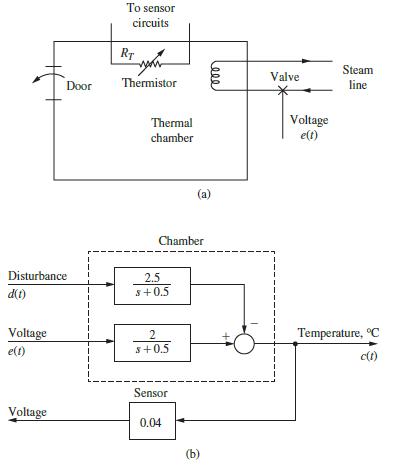

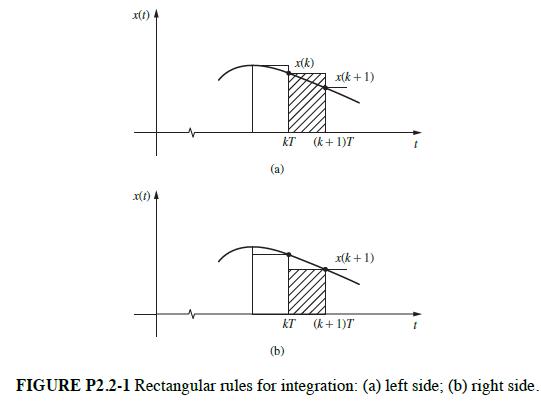


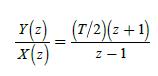
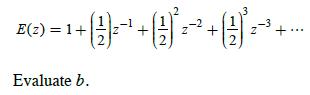
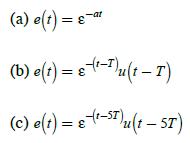


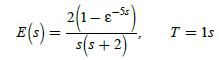


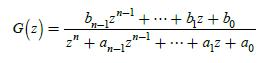
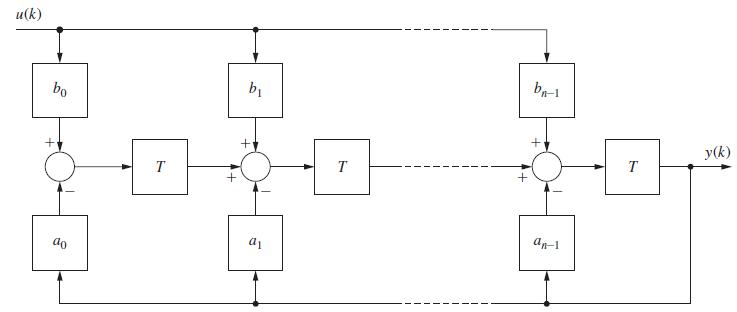
![100 1 (k+1)= 1 1 0 (k) 1 1 0(k) + ou(k) | 010 0 y(k)= [001]x(k)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/4/0/4/81865a669928b1a71705404817516.jpg)