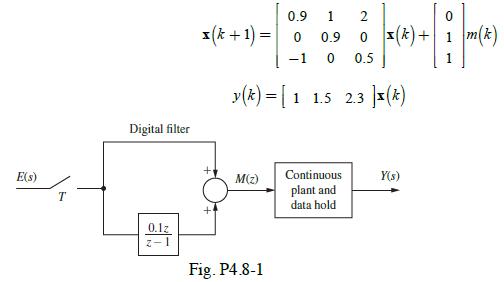
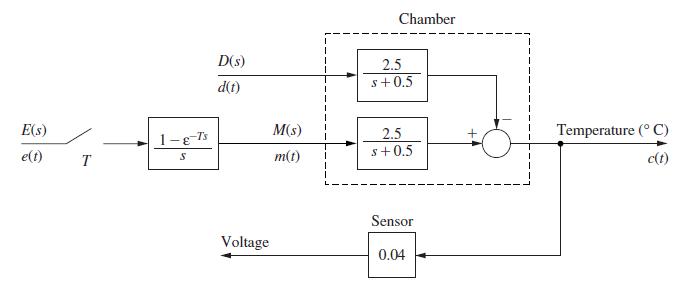
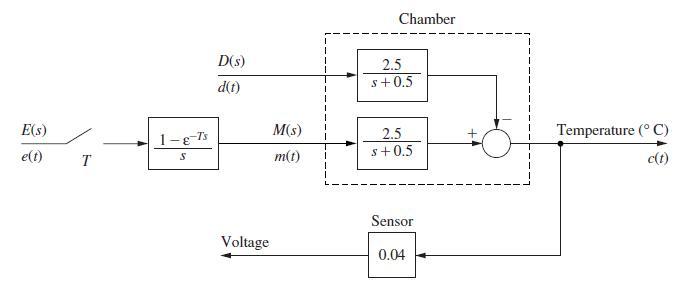
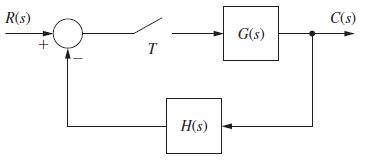
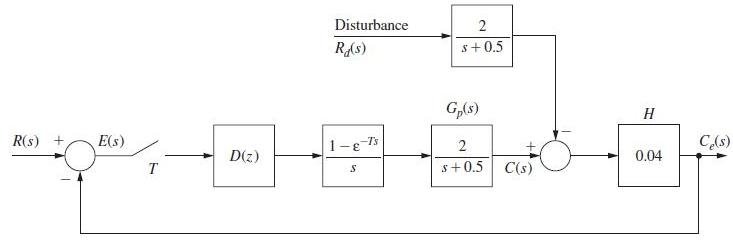
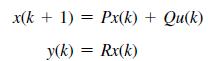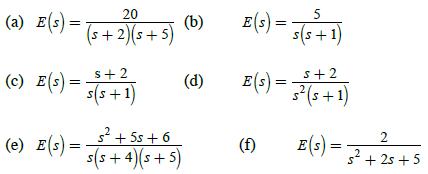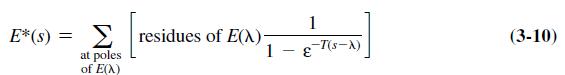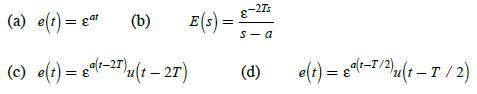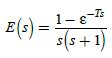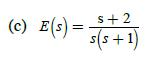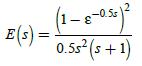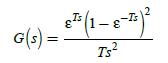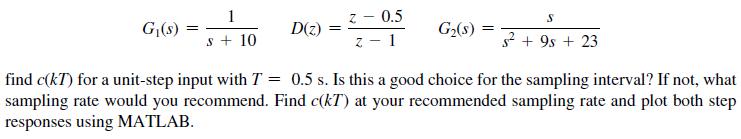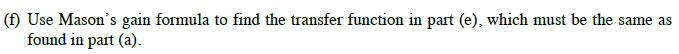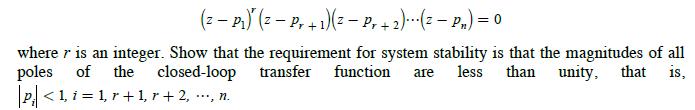![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


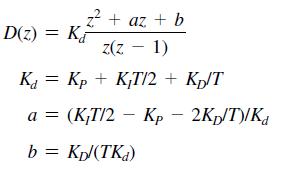







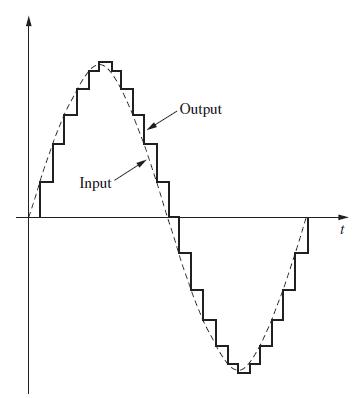
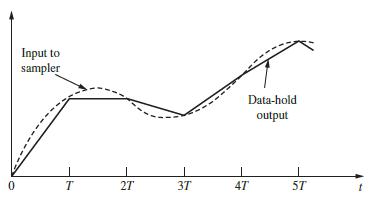
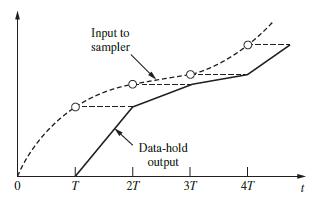
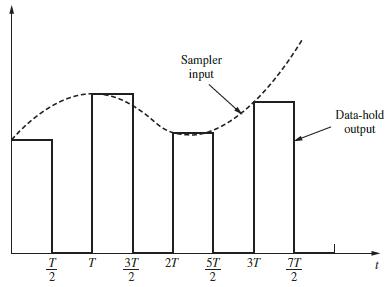
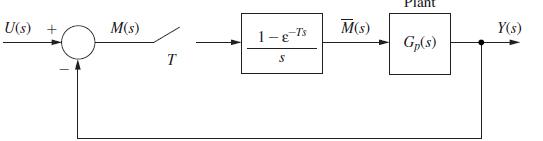
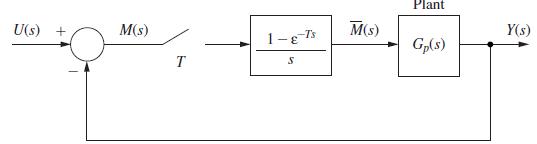
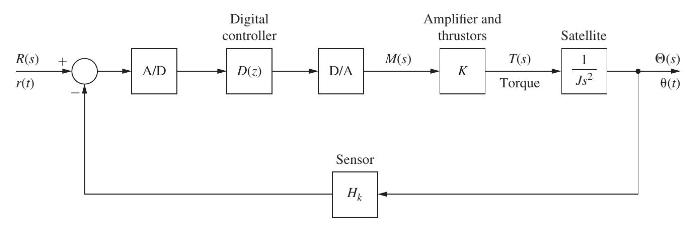
![U(s) T= 0.1 s FIGURE 11-2 Servomotor system. 1 0 2= [8] P(2) = Q = 1--Ts S 1 s(s+ 1) Y(s)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/5/7/9/82565a9153154fb91705579825191.jpg)
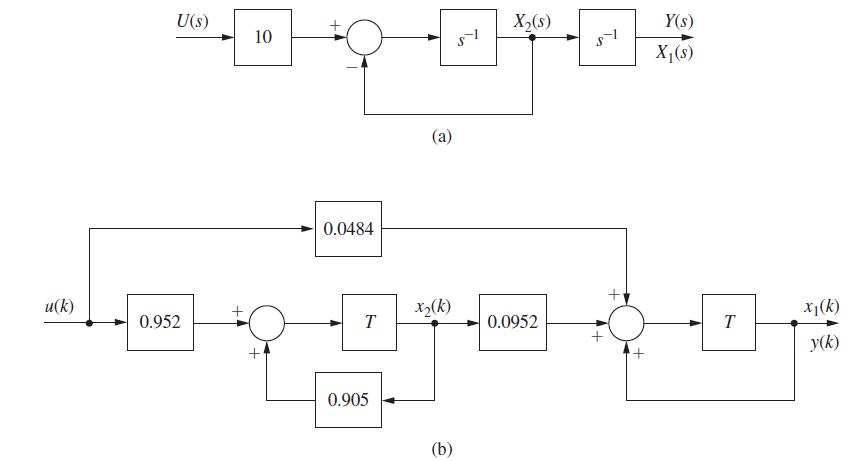
![x(k + 1) y(k) = = 1 0 [1 0.095163 0.904837 0]x (k) x(k) + 0.0048374 0.095163 u(k) (9-1)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/5/7/9/86765a9155b7149a1705579867383.jpg)
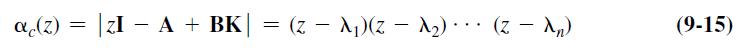

![G(z.) N N 1 [s (s + 1)] = 0.00484Z+0.00468 z1.905z + 0.905](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/5/8/2/25865a91eb2912911705582258072.jpg)
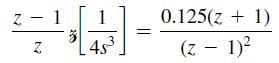
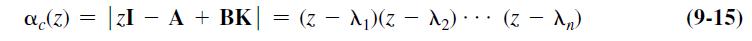
![K = [00 01][B AB.. A B A B a (A) (9-25)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/5/8/3/96365a9255b6771e1705583962774.jpg)
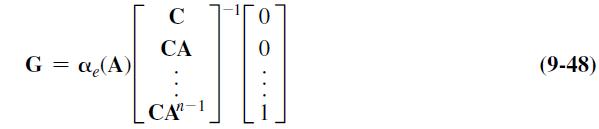
![x(k+ 1) A B]=[Gc q(k+ 1). GC - BK x(k) BK ][ N(6)] AGC BK (9-56)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/5/8/4/08665a925d63e5341705584085637.jpg)
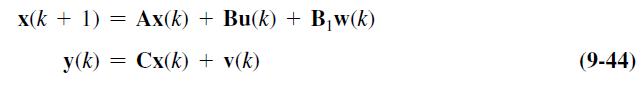
![G(z.) = N Z 1 [s (s + 1)] = 0.00484Z+0.00468 z1.905z + 0.905](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/5/8/4/20265a9264aea0de1705584202729.jpg)
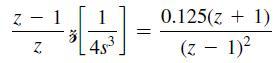



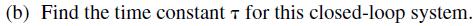
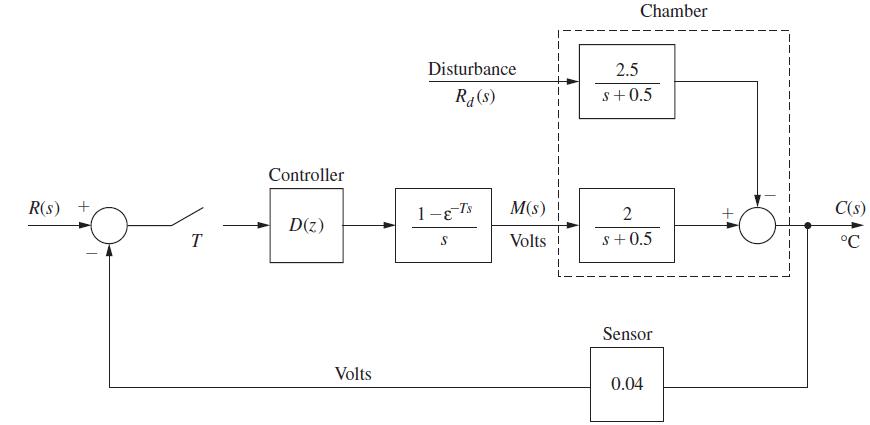
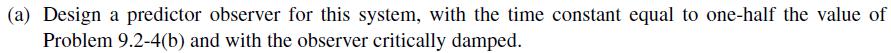

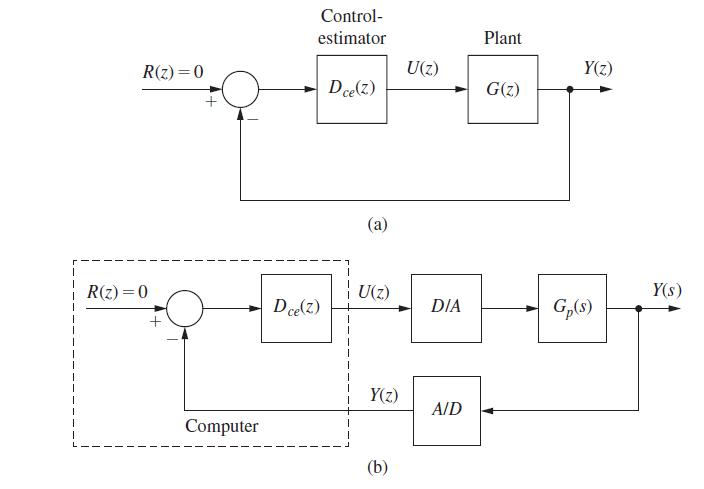
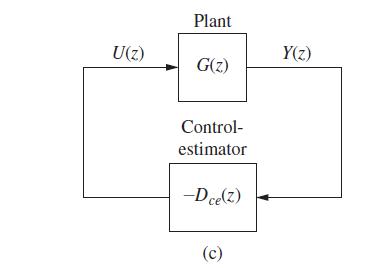
![B]=[GCA x(k+ q(k+ 1). -BK A - GCA x(k) BKq(k) (9-74)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/6/4/0/49765aa023163fc01705640496295.jpg)
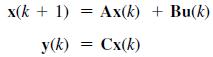
![x(k + 1) = Suppose that the output is given by 1 0.0952 0.00484 0.9048] 0.0952|u(k) x(k) + y(k) = [0 1]x(k)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/6/4/0/63665aa02bc37dd61705640635156.jpg)

![0.0048374 0.095163 Then the gain matrix is, from (9-25), K = [0 1] [B AB] = -95.082 105.082 0.0138934](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/6/4/0/77465aa0346198d91705640773013.jpg)
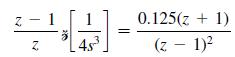
![x(k+ 1) : - 0 = x(k) + y(k) [10]x(k) = [0.125 25 Ju(k) 0.25](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/6/4/1/03165aa0447db13c1705641030598.jpg)