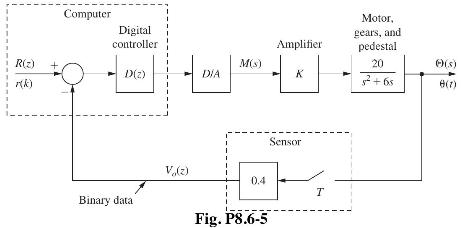
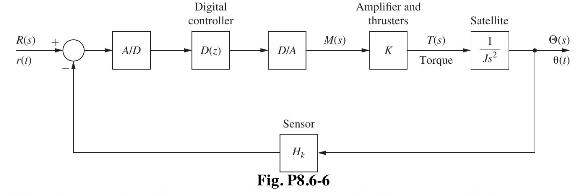
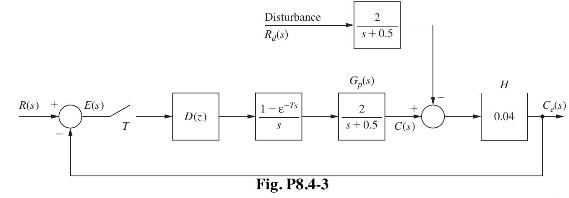
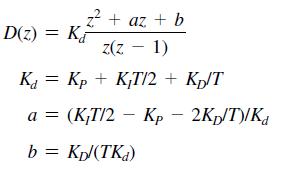![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


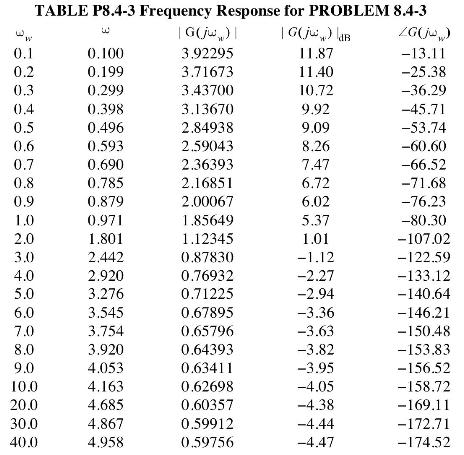
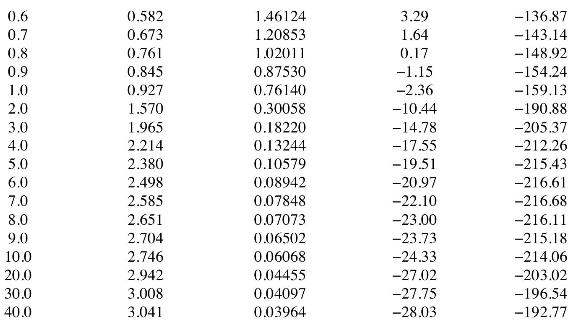
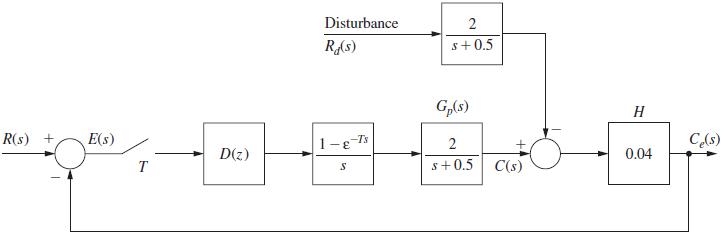
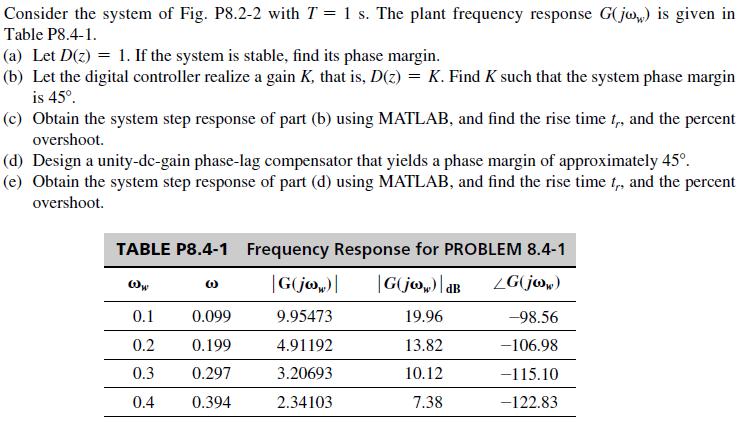
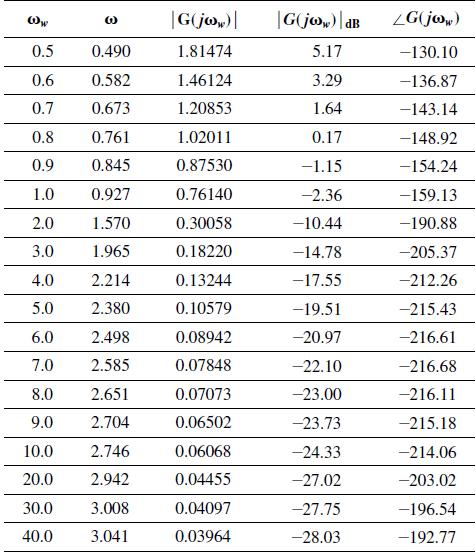
![It is shown in [6] that given the partitioned matrix H DE F G where each partition is nX n, the determinant](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/5/6/6/30465a8e0608f50a1705566303926.jpg)
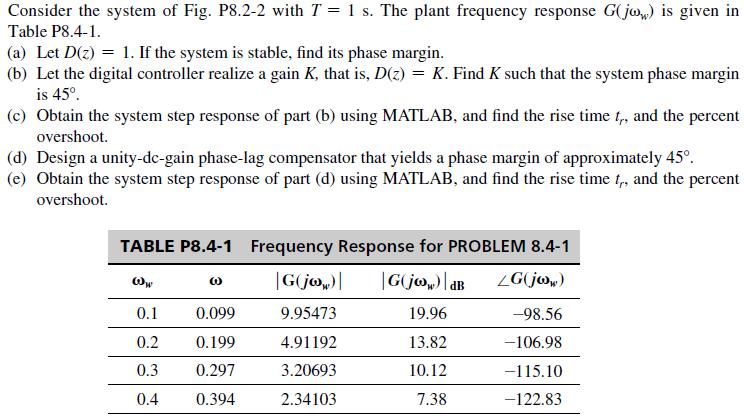
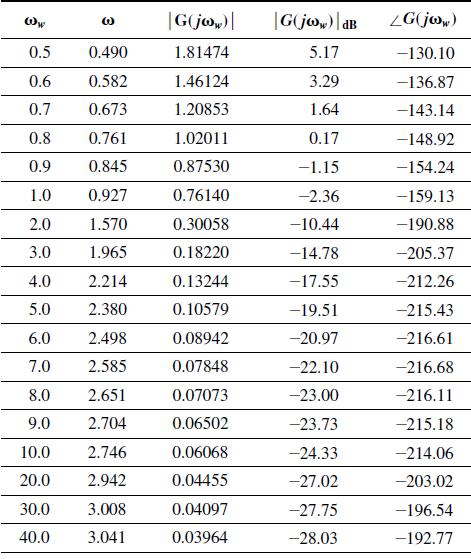

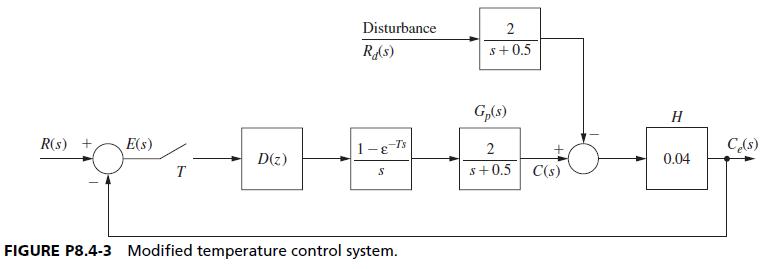


![It is shown in [6] that given the partitioned matrix H = E F G where each partition is n X n, the](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/5/8/0/41365a9177d8f9bf1705580413336.jpg)
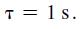
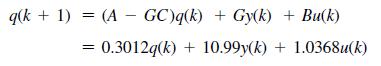
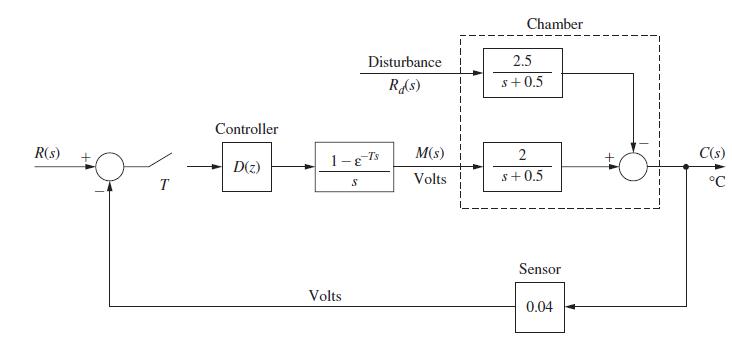
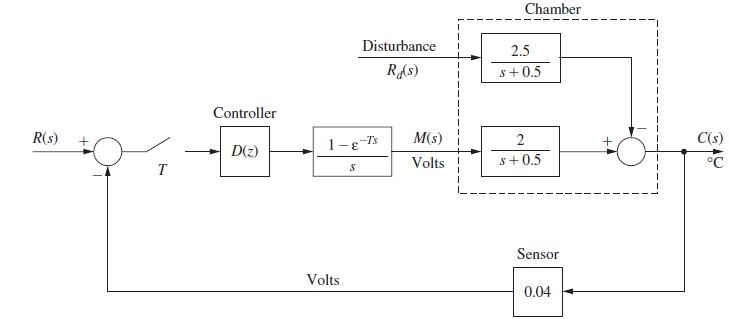
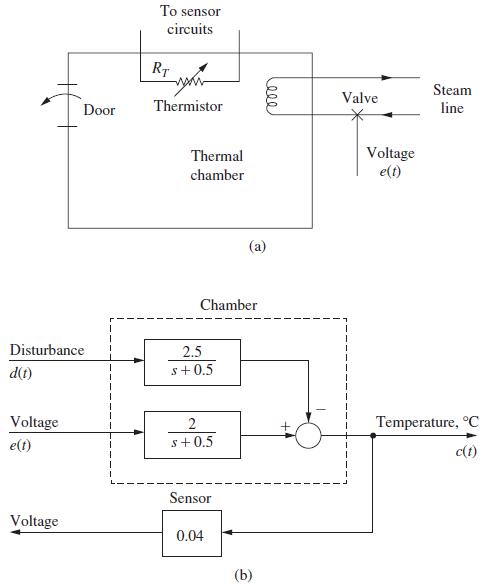
![(0.04)- 2 s(s+ 0.5)] = 0.04147 z - 0.7408 Note that the sensor gain is included in this transfer function.](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/6/4/1/20465aa04f44d6fc1705641202963.jpg)
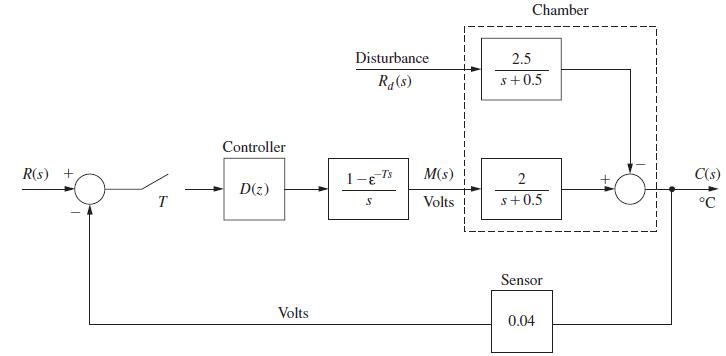
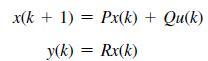

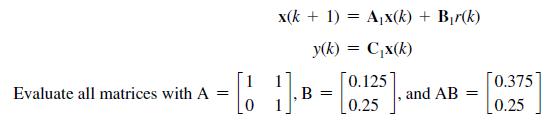
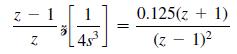
![R(s) r(t) where x(k) is angular position and x2(k) is angular velocity. + x(k + 1) = = [61]8) + [0.25 (4) (a)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/6/4/1/60665aa0686364641705641605084.jpg)
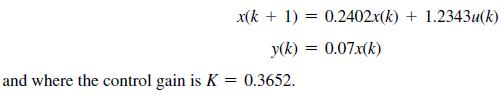
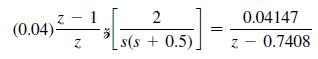
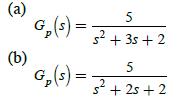






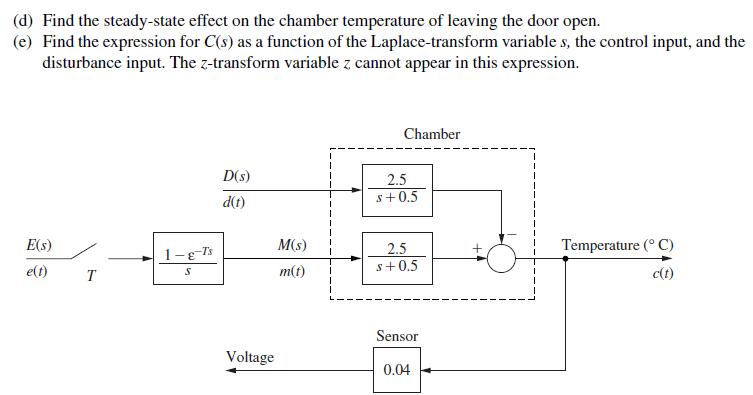
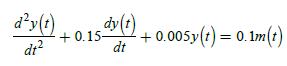

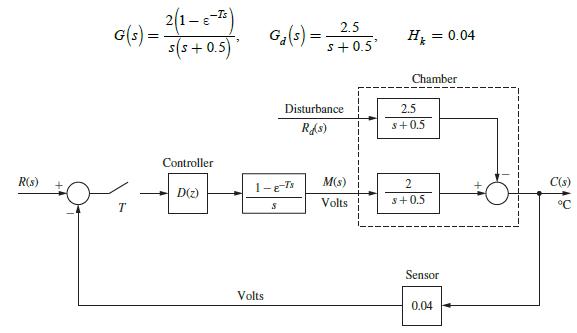
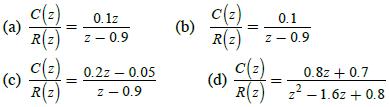

![R(s) E(S) T= 1 s D(z) 1-8-7's S M(s) Gp(s) 1 s+1] C(s)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/4/8/8/16965a7af298dc5a1705488169103.jpg)
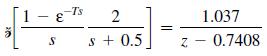
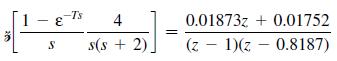
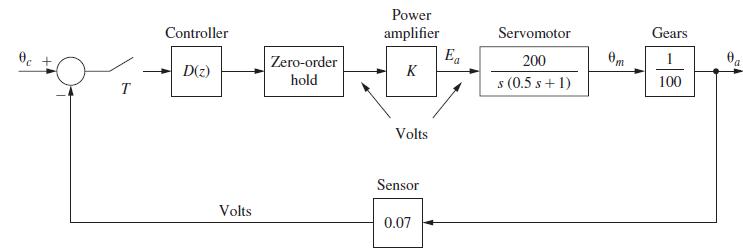

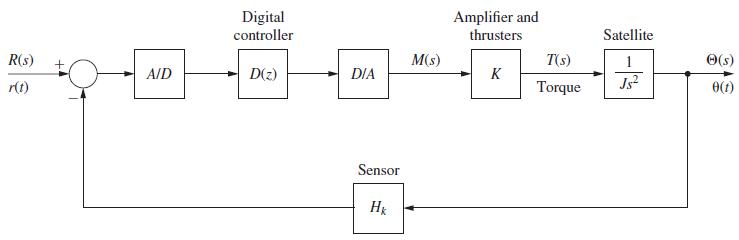
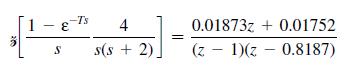
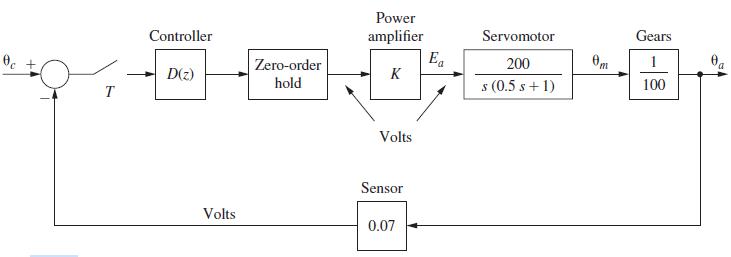







![10 2 (6 85 / (4) + / 3 /-(4) 0 0.5 x (k+ 1) = y (k)=[ 1 2 ]x (k)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/4/0/4/57665a668a0620501705404574781.jpg)
![1 (* + 1) = [ 0 ] (*) + [ (*) 3 y (k)=[-2 1 ]x(k)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/4/0/4/28365a6677b05d0c1705404282032.jpg)
![01 (+)-x(*)+-(*) 1) = 03 y(k)=[-2 1 ]x(*)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/4/0/5/31365a66b81119601705405311527.jpg)
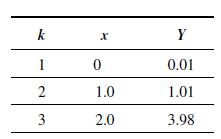

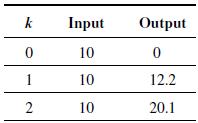


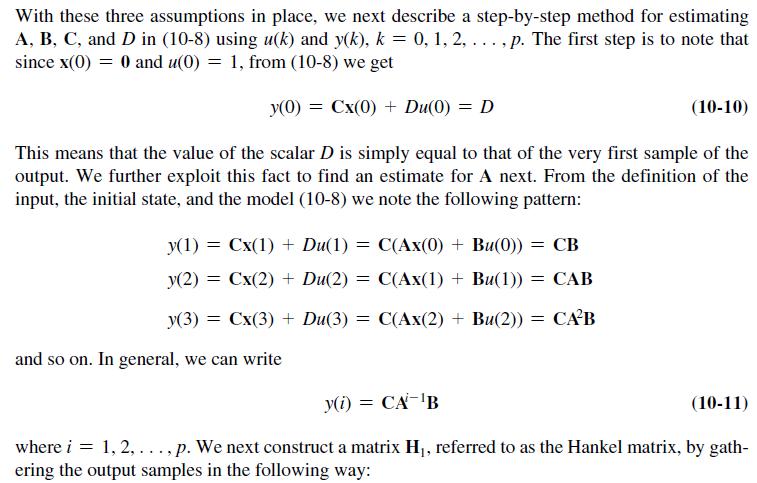
![where A x(k+ 1) = Ax(k) + Bu(k) y(k) = Cx(k) 0 -[-2-3] = B = -A C = [01]](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/6/4/3/65365aa0e8577d551705643651451.jpg)
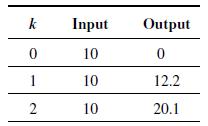
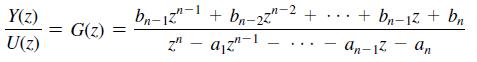
![P(N + 1) = P(N) - P(N)f(N + 1) Y Y [ 1/2+ X + + F7(N + 1) = P(N)E(N + 1)] *'F*(N + 1) = P(N) a Y (10-56)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/6/4/4/40765aa1177b13c91705644406586.jpg)
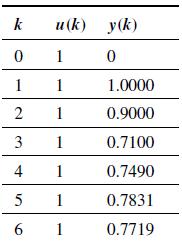
![y=[0; 1; 0.9; 0.71; 0.749; 0.7831; 0.7719]; u=ones (length (y), 1); T=0.1; % Create a data object using the](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/6/4/4/65365aa126d0f25f1705644651976.jpg)

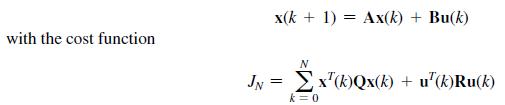
![with the cost function x(k+ 1) = 0.6x(k) + 0.5u(k) 3 J3 = [2x(k) + 7u(k)] k = 0](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/6/4/5/66365aa165f427181705645662333.jpg)
![with A = 208 0 0 0 3 0 -8 -6 x = Ax + Bu y = Cx 0 B = 0, and C= [1 0 0]. Using = 8 0 0 0 6 0 0 4 3 R = 1.5](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/6/4/6/01865aa17c25a3141705646016987.jpg)
![with the cost function x(k+ 1) = Ax(k) + Bu(k) N JN = [Qx(k) + Ru(k)] k=0](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/6/4/6/40665aa1946d01db1705646405621.jpg)
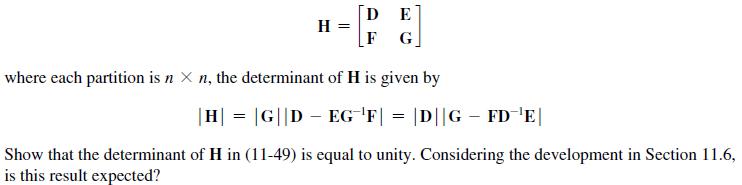
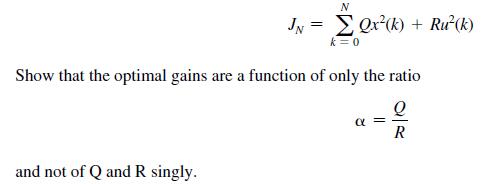
![x(k + 1) [ = 0.999946 -0.177854E-1 y(k) [21]x(k) + v(k) 0.592847E 2] 0.976233 2xCA x(k) + [0.178567E 4](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/6/4/7/61065aa1dfa5ee561705647609045.jpg)
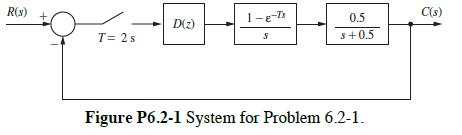
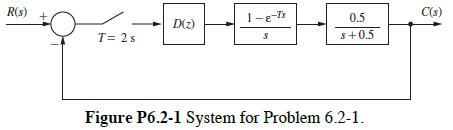
![where G(2) is defined as C(z) = G(z) 1 + G(z) -R(z) -Ts G(z) 0 = [1-8,4] - - 1 = S s +2 ss 4 +2)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/6/5/1/99565aa2f1b87d7c1705651993885.jpg)
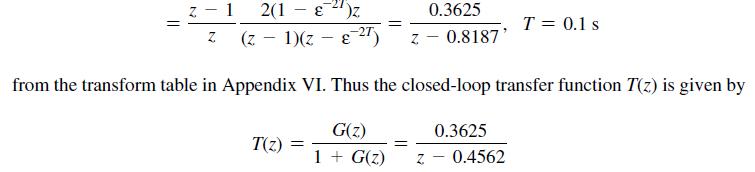
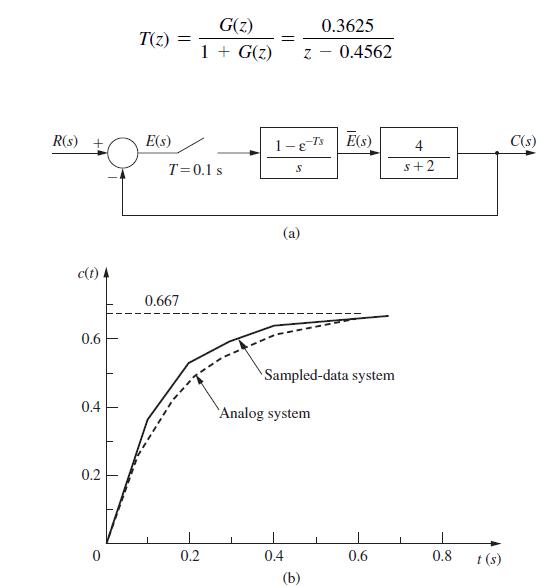
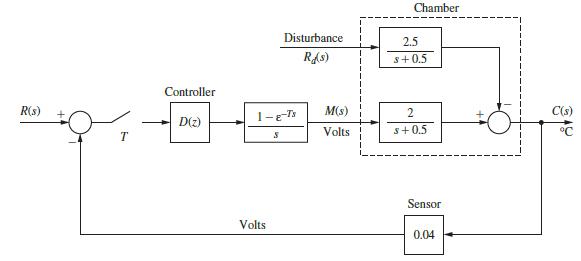
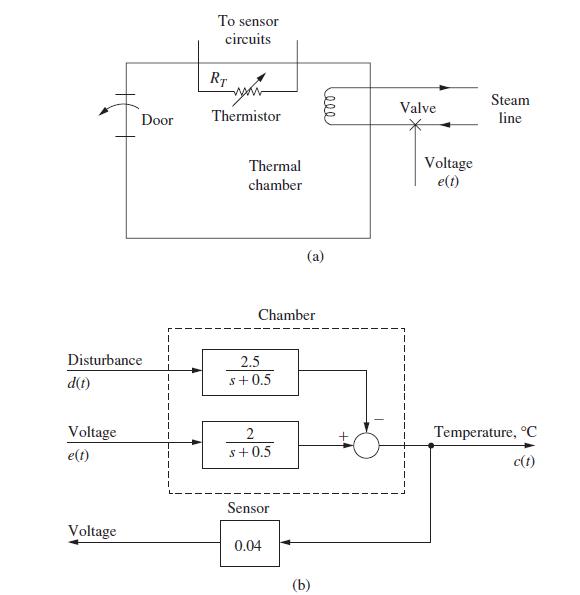
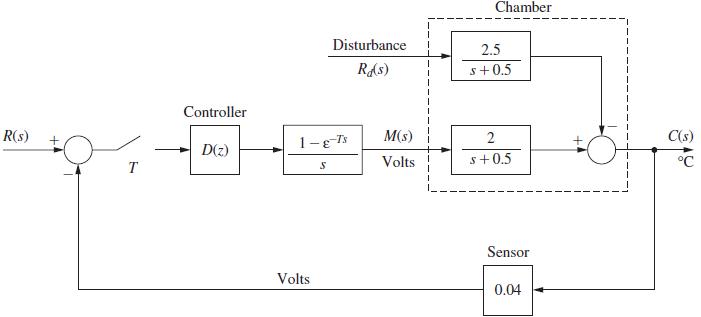
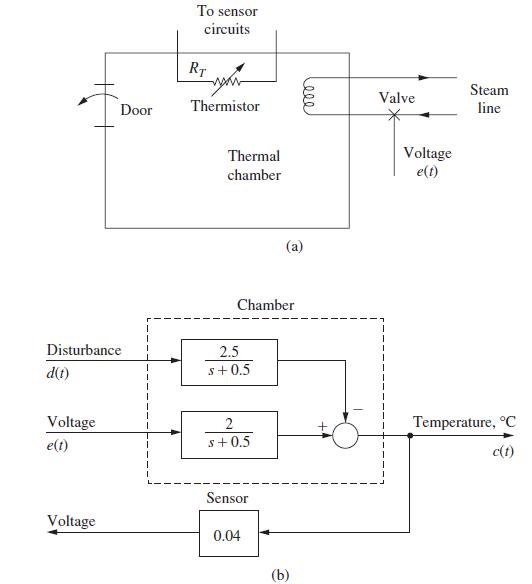
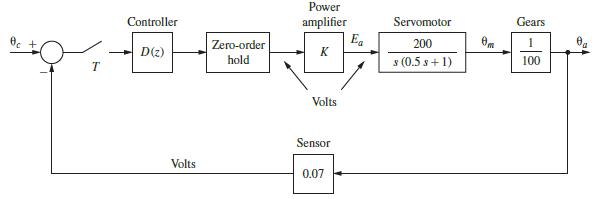
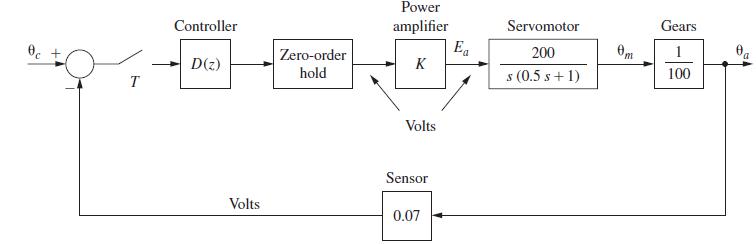
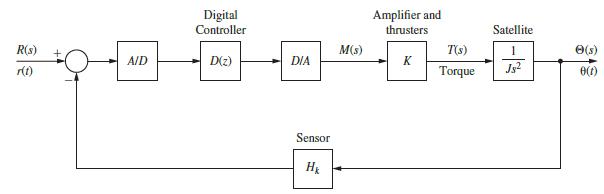
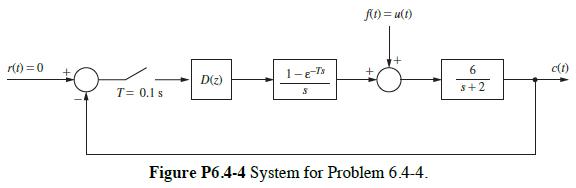
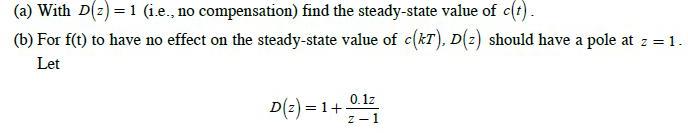

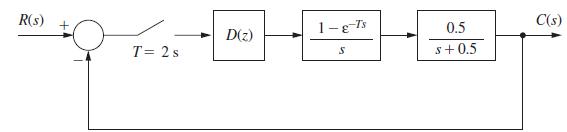
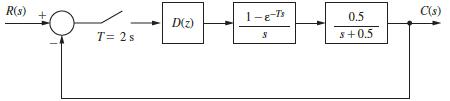
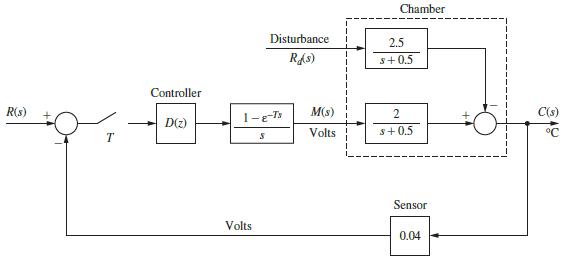
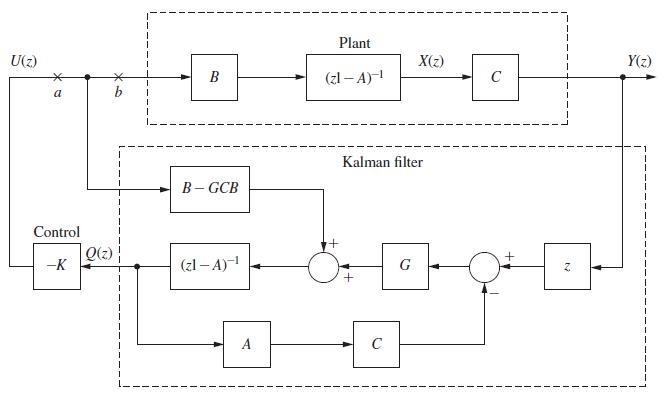
![R(s) m(kT) = e(kT) - 0.9e[(k 1)T] + m[(k 1)T] Gp(s) 1 s+1 T= 1 s D(z) 1-8-7's S M(s) Figure P6.5-2 System](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/5/6/0/64965a8ca49e2c881705560649848.jpg)