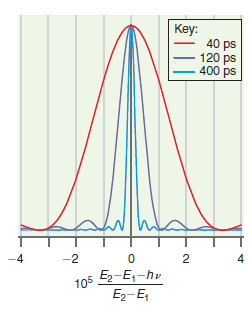
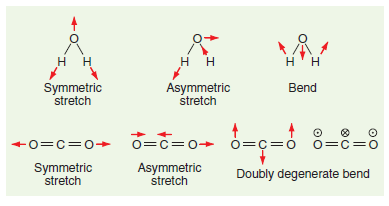
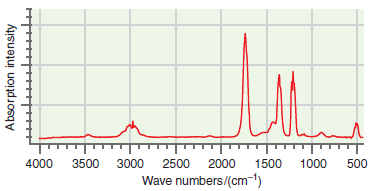
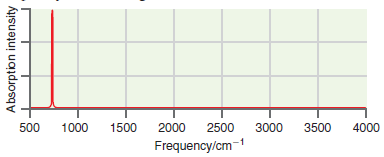
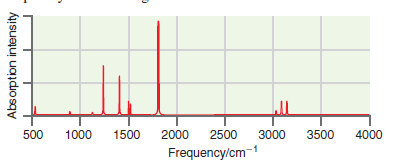
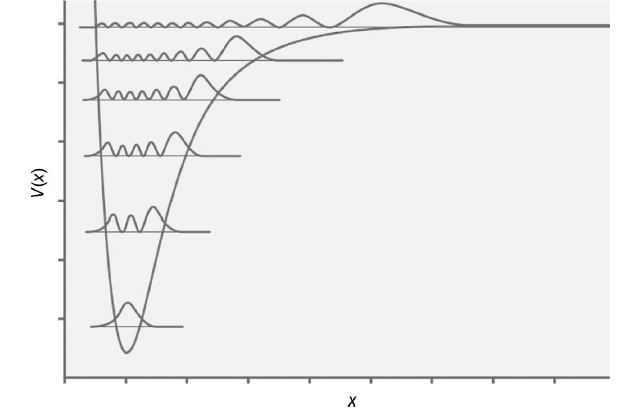
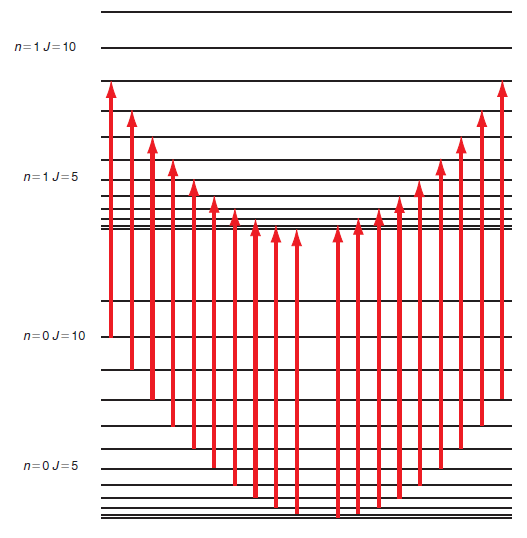
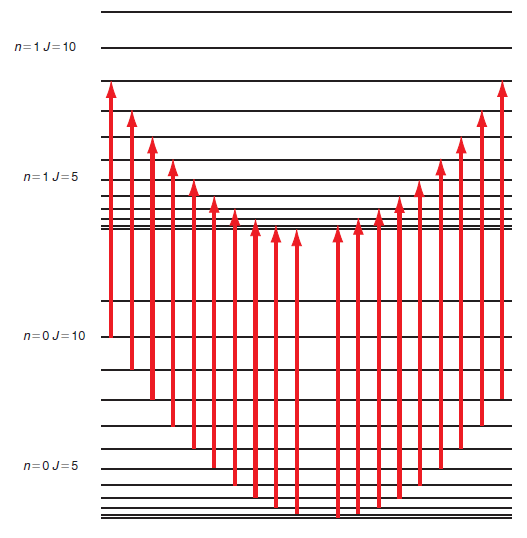
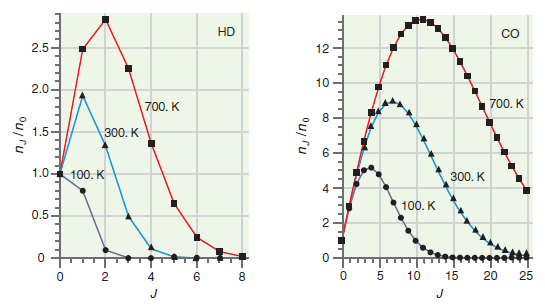
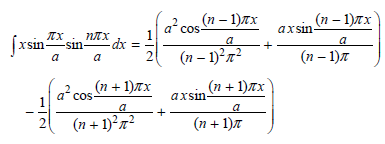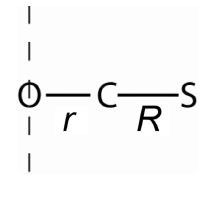![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


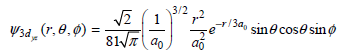
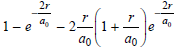
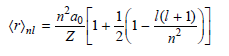
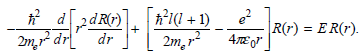
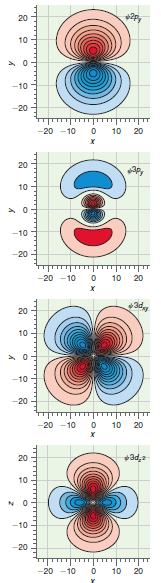
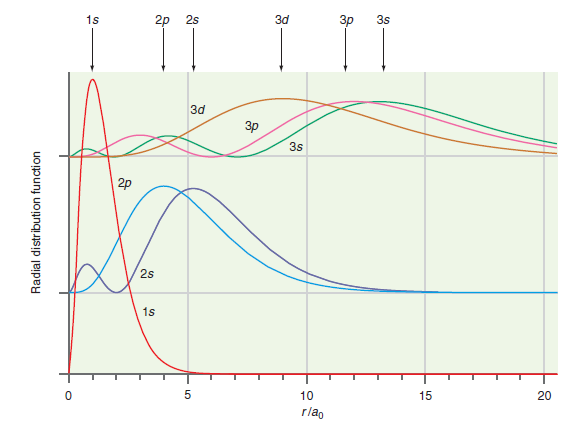
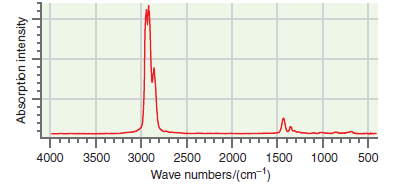
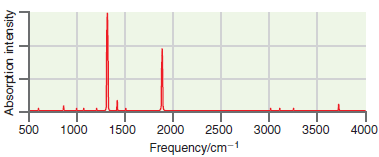
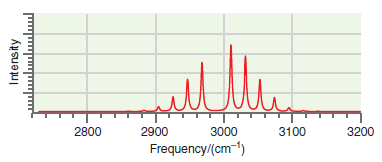
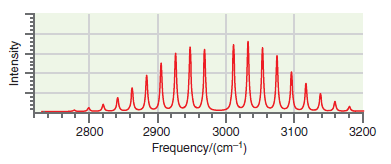
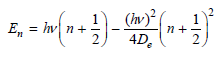
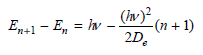
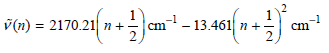
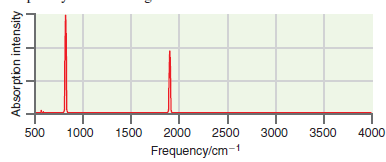
![A) = 20 A(t) = (1 + e5())exp[i(kyp – wt)] %3D](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1525/3/4/1/0615aeadb85026531525341046446.jpg)
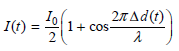
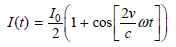
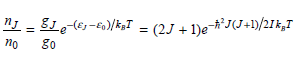
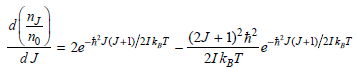
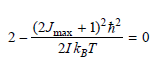
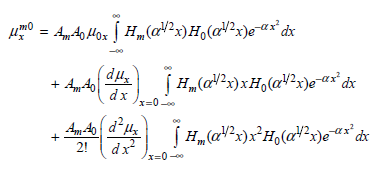
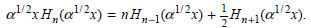
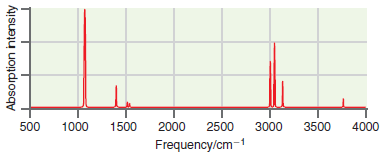
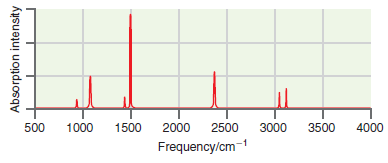
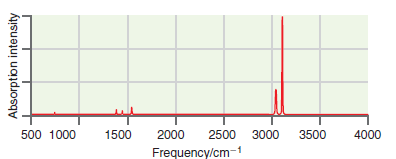
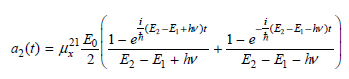
![оiОда, ) — Е Ги7sin'(E, - E - i)2H] (E, – E, – hv)?](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1525/3/4/0/8025aeada829f7e61525340789755.jpg)