![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()



![Instruction [25-0] Jump address [31-0] Shift left 2 26 28 0. PC + 4 [31-281 Add Add ALU result Shift left 2 RegDst Jump](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1544/5/3/2/4615c0fb1ed1969c1544515022341.jpg)


![Row 1 [1, 2, 0, 0, 0, 0] Row 2 [0, 0, 1, 1, 0, 0] Row 3 [0, 0, 0, 0, 9, 0] Row 4 [2, 0, 0, 0, 0, 2] Row 5 [0, 0, 3, 3, 0](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1544/6/0/7/0655c10d559e38871544534990373.jpg)




![BinarySearch(A[0..N-1], X) { low = 0 high = N -1 while (low <= high) { mid = (1ow + high) / 2 if (A[mid] style=](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1544/6/0/6/8865c10d4a6538ac1544534810652.jpg)
![struct entry { int srcIP; char URL[128]; // request URL (e.g. , “GET index.html](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1544/5/3/9/9465c0fcf2a9d50f1544522507321.jpg)







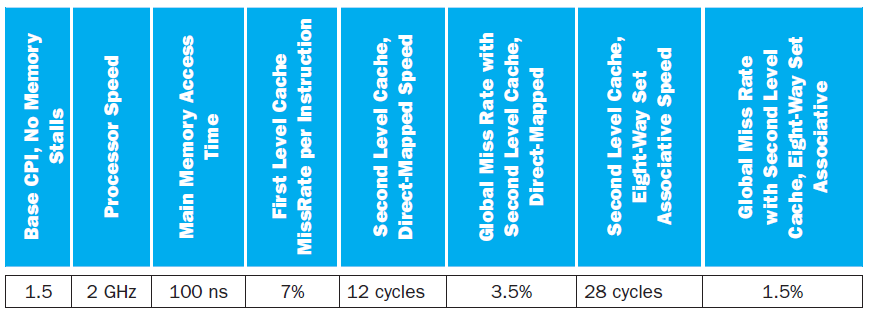








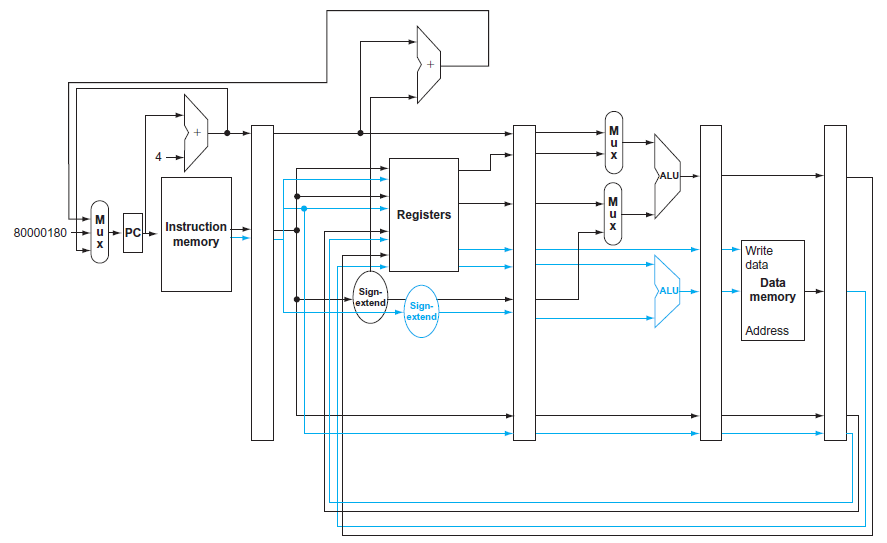
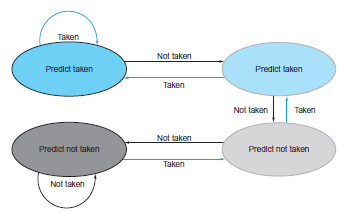



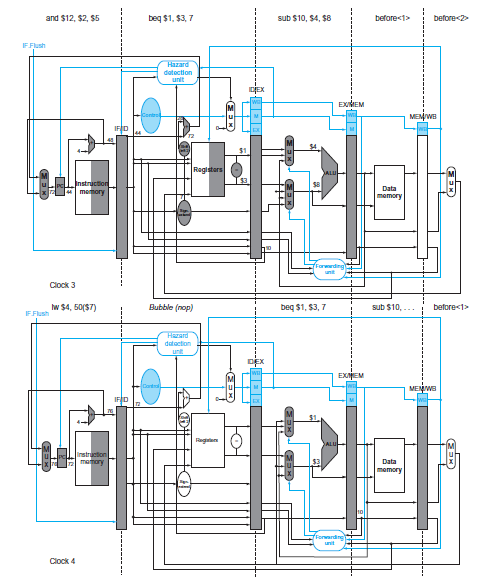

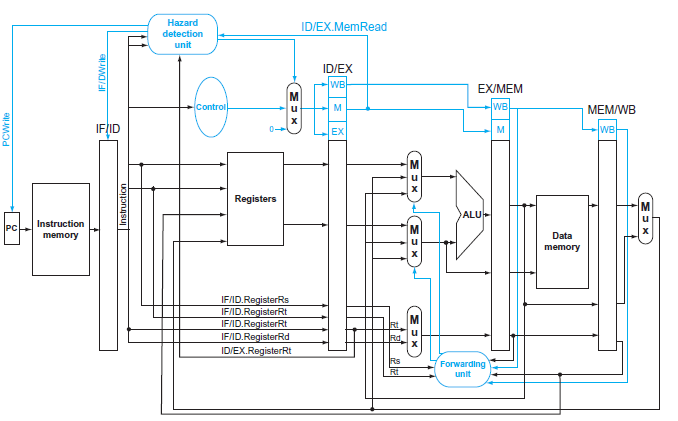
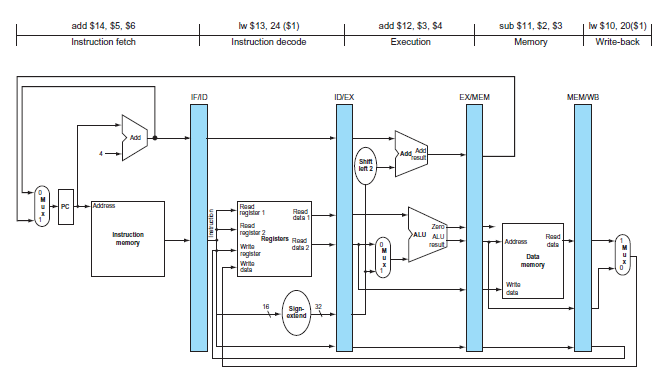

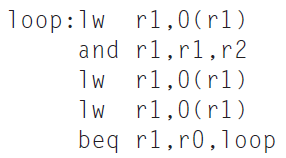


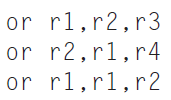



![Jump address [31-0] Instruction [25-0] Shift left 2 26 28 0. PC + 4 [31-281 Add ALU result Add Shift left 2 RegDst Jump](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1544/5/3/2/2375c0fb10d8a54d1544514798788.jpg)


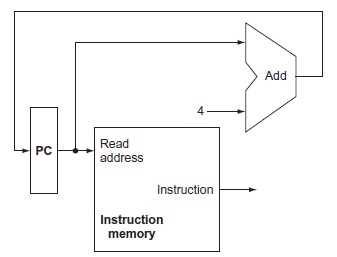
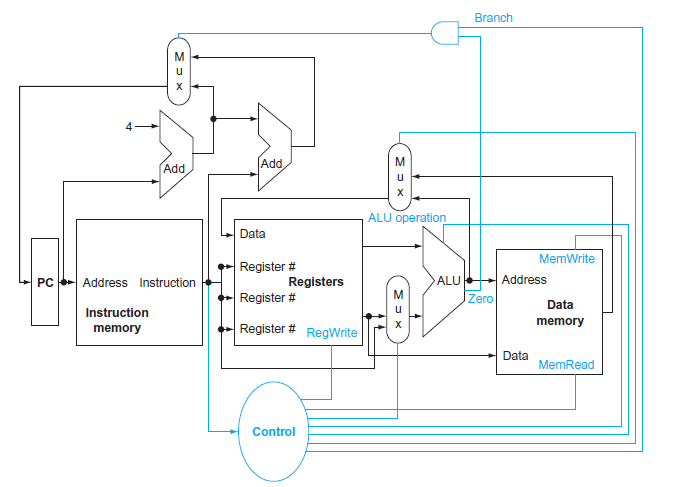
![for (i= 3;i<128;i++) sig_out[i]=sig_in[i-3] +sig_in[i-1] * f[2]+sig_in[i] * f[3]; * f [0]+sig_in[i- 2] * f[1]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1544/5/2/3/3345c0f8e4651f901544505895410.jpg)