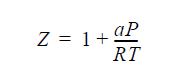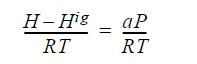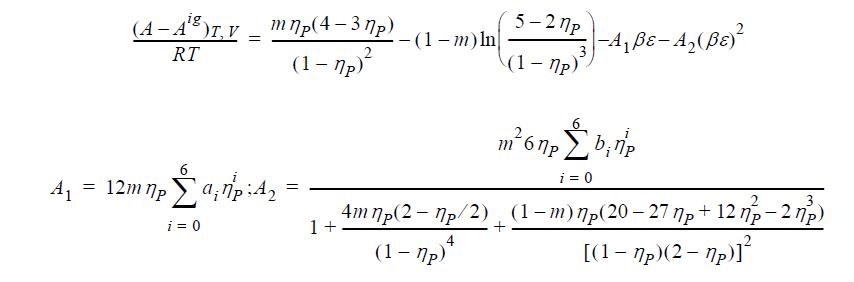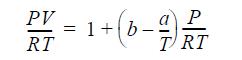![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()



![T AGR (77) + ACp[(T-TR) - Tln (77)]- [T-TR T R T R AHR TR AGT= AGR](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1696/2/4/2/685651a9bfdd0f751696242682781.jpg)
![[U] [M] -ACP R T [(-4) - ()]-[-4] 1- Inf T TRASR AS TR Tr R](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1696/2/4/2/840651a9c986dd071696242839477.jpg)

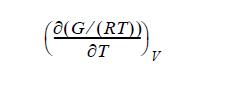
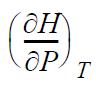
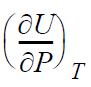
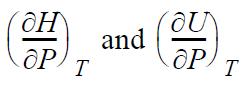
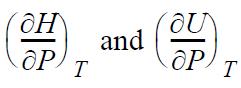
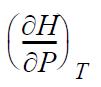
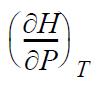
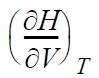
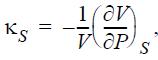

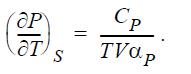
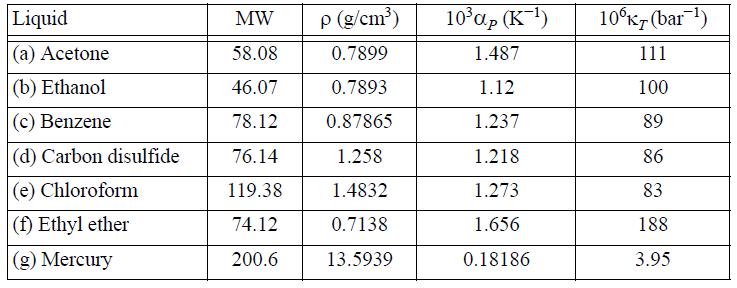

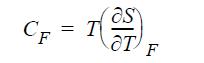
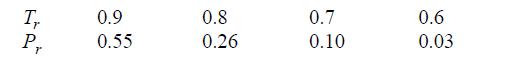
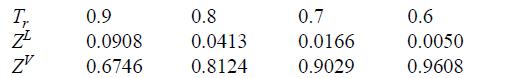
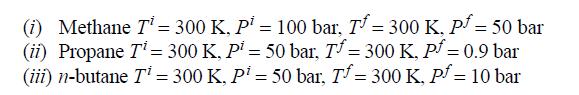
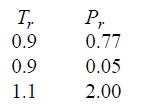
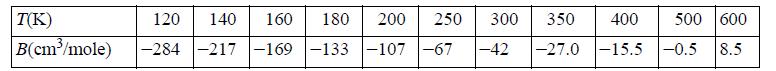

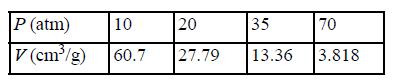
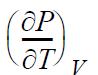
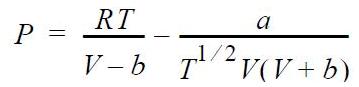
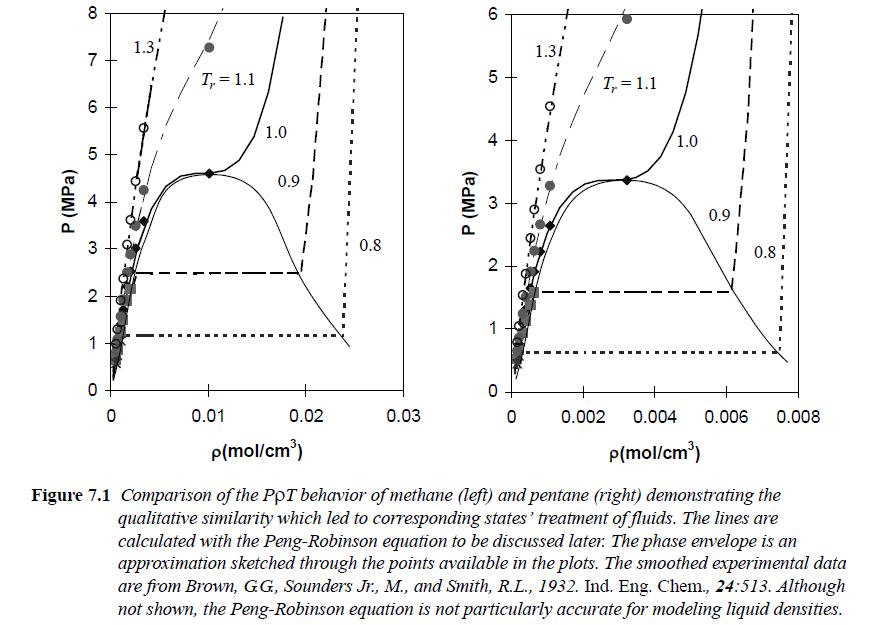
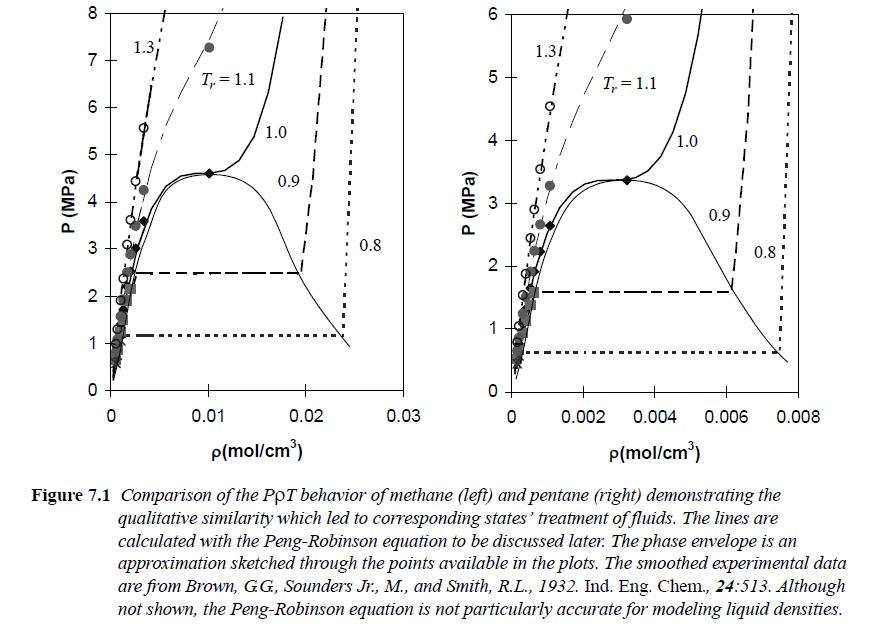
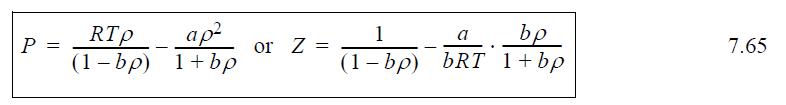
![RT a=a_a; a = 0.42748- q=0.4274 2 C a = [1 + K(1-T)] Pc RT b=0.08664- K = 0.480+ 1.574 - 0.1760 Po C 7.66](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1696/0/5/9/7416517d15d432b31696059738510.jpg)
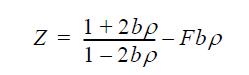
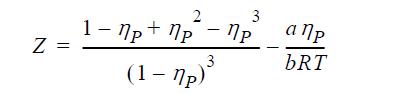
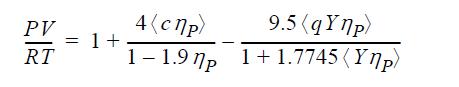


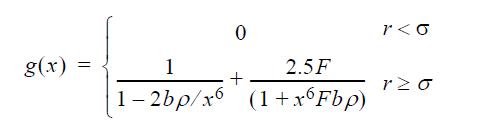
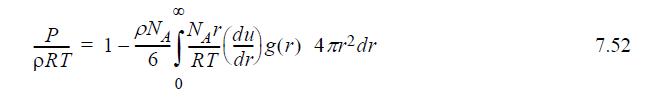
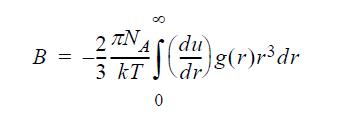
![u(r) exp[-] lim g(r) exp P0 7.57](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1696/0/6/2/5176517dc35409411696062515236.jpg)
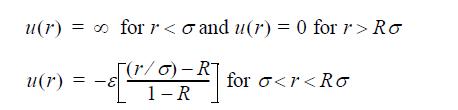
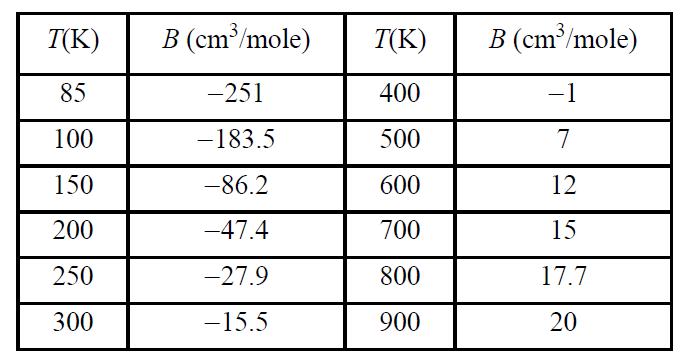
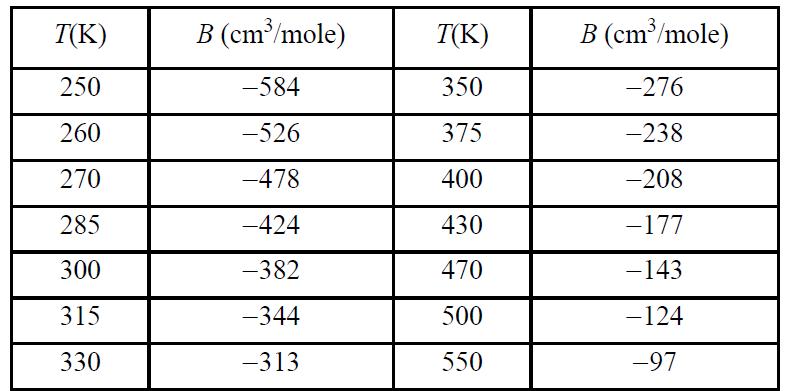
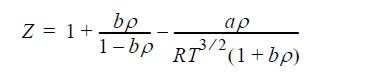
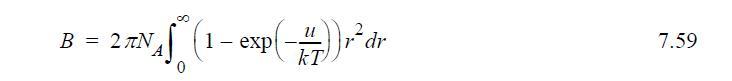


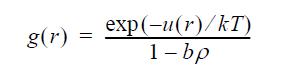
![Z=1+ bp 1+bp -p[exp(a/T)-1]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1696/0/6/3/5796517e05b227361696063579933.jpg)
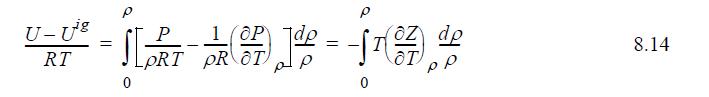
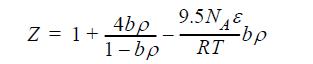
![P H-Hig (HF) --1), # RT OT p P = P (S-siz) (S-5) = - [ (z - 1) + 7 (7) ] / -107), (Z- T P 0 8.29 8.30](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1696/0/7/3/397651806b580e1a1696073366000.jpg)